[笔记整理] Task2 - 数据分析 EDA
Task2 - 数据分析 EDA定义步骤1. 载入各种数学科学以及可视化库2. 载入数据step1: 载入训练集和测试集step2: 简略观察数据3. 数据总览step1: 数据的相关统计量step2: 熟悉数据类型4. 判断数据缺失和异常step1: 每列存在 NAN 的情况 ---可视化step2: 查看异常值检测5. 了解预测值的分布step1: 预测值的总体分布step 2: 查看偏度和峰度step 3: 预测值的具体频数6. 特征 features7. 数字特征分布step 1: 相关性分析step 2: 查看几个特征的偏度和峰值step 3: 每个数字特征的分布可视化step 4 : 数字特征相互之间的关系 可视化step 5: 多变量互相回归关系 可视化8. 类型特征分析step 1: unique 分布step 2: 类别特征 箱型图可视化step 3: 类别特征的小提琴可视化step 4: 类别特征的柱形图可视化step 5:类别特征的每个类型 频数可视化9. 用Pandas_profiling生成数据报告
定义
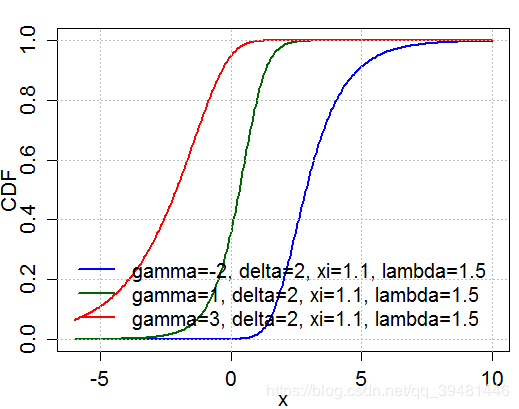
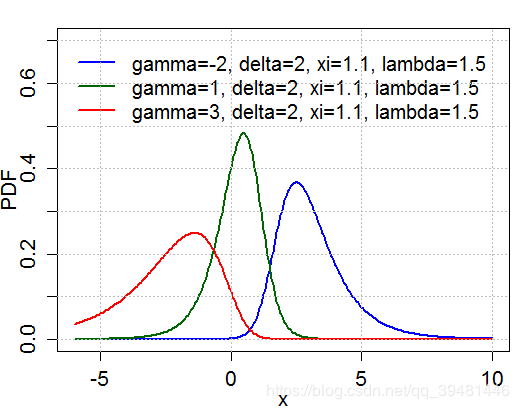 Cumulative distribution function
Cumulative distribution function
 seaborn的displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。
seaborn的displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。
作者:Scarlett_can
数据探索性分析
EDA:(Exploratory Data Analysis 熟悉数据集,了解数据集,对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用 步骤 1. 载入各种数学科学以及可视化库 数据科学库: pandas、numpy、scipy; 可视化库: matplotlib、seaborn、plotlyNotes:
#导入warning包,利用过滤器来实现忽略警告语句
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno # 缺失值可视化处理
import plotly.express as px
import plotly.io as pio
pio.templates.default = 'plotly_white'
2. 载入数据
step1: 载入训练集和测试集
step2: 简略观察数据
step1: 载入训练集和测试集
Notes:
header : 指定行数用来作为列名,数据开始行数。 如果文件中没有列名,则默认为0【第一行数据】,否则设置为None。 如果明确设定 header = 0 就会替换掉原来存在列名。 header参数可以是一个list例如:[0,1,3],这个list表示将文件中的这些行作为列标题(意味着每一列有多个标题),介于中间的行将被忽略掉。 注意:如果skip_blank_lines=True 那么header参数忽略注释行和空行,所以header=0表示第一行数据而不是文件的第一行。 skiprows :需要忽略的行数(从文件开始处算起),或需要跳过的行号列表(从0开始) skip_blank_lines :如果为True,则跳过空行;否则记为NaN prefix:在没有列标题时,也就是header设定为None,给列添加前缀。例如:添加prefix= ‘X’ 使得列名称成为 X0, X1, … index_col :用作行索引的列编号或者列名,如果给定一个序列则有多个行索引path = '../data/'
Train_data = pd.read_csv(path + 'used_car_train_20200313.csv', sep=' ')
Test_data = pd.read_csv(path + 'used_car_testA_20200313.csv', sep = ' ')
step2: 简略观察数据
Notes:
head()+shapeTrain_data.head().append(Train_data.tail())
Train_data.shape
Test_data.head().append(Test_data.tail())
Test_data.shape()
3. 数据总览
通过describe() 来熟悉数据的相关统计量
通过info() 来熟悉数据类型
step1: 数据的相关统计量
Notes:
count ; mean; std ; min ; medium; 25%; 50%; 75%; max; 目的: 瞬间掌握数据的大概的范围以及每个值的异常值的判断 比如有的时候会发现 999,9999,-1 等值,这些其实都是nan的另外一种表达式Train_data.describe()
Test_data.describe()
step2: 熟悉数据类型
Notes
info(): 了解数据每列的type; 有助于了解是否存在除了nan以外的特殊符号异常Train_data.info()
Test_data.info()
4. 判断数据缺失和异常
查看每列的存在nan情况
异常值检测
step1: 每列存在 NAN 的情况 —可视化
Train_data.isnull().sum()
Test_data.isnull().sum()
Notes:
查看 NAN 存在的个数是否真的很大 如果很小,一般选择填充; 如果使用 LGB 等树模型可以直接空缺,让树自己去优化 但如果 NAN 存在的过多,可以考虑删除改特征 可视化展示的几种方式 Matrix:使用最多的函数,能快速直观地看到数据集的完整性情况,矩阵显示 如果数据是时序的,那可以用freq参数 最多支持50列 Bar:简单的展示无效数据的条形图 Heatmap: 两个变量的无效相关范围从-1(如果一个变量出现,另一个肯定没有)到 0(出现或不出现的变量对彼此没有影响)到1(如果一个变量出现,另一个肯定也是) 大于-1和小于1表示有强烈的正相关和负相关,但是由于极少数的脏数据所以并不绝对,这些例外的少数情况需要在数据加工时候予以注意 热图方便观察两个变量间的相关性,但是当数据集变大,这种结论的解释性会变差msno.matrix(Train_data.sample(250)) # why need sample?
msno.bar(Train_data.sample(1000))
msno.heatmap(Train_data)
step2: 查看异常值检测
Train_data['notRepairedDamage'].value_counts() #‘ - ’也为空缺值
Train_data['notRepairedDamage'].replace('-',np.nan,inplace=True)
# 因为很多模型对nan有直接的处理,这里我们先不做处理,先替换成nan
Train_data['notRepairedDamage'].value_counts()
# 对Test data做同样的处理
Test_data['notRepairedDamage'].value_counts()
Test_data['notRepairedDamage'].replace('-',np.nan,inplace=True)
Notes:
类别特征严重倾斜,一般不会对预测有什么帮助,可以先删掉Train_data["seller"].value_counts()
Train_data["offerType"].value_counts()
del Train_data["seller"]
del Train_data["offerType"]
del Test_data["seller"]
del Test_data["offerType"]
5. 了解预测值的分布
总体分布概况(无界约翰逊分布等?)
查看skewness and kurtosis
查看预测值的具体频数
step1: 预测值的总体分布
Notes:
Johnson‘s SuS_uSu - distribution Wiki: Johnson proposed it as a transformation of the normal distribution Application: Johnson’s SuS_uSu-distribution has been used successfully to model asset returns for portfolio management. Probability density function Cumulative distribution function
Cumulative distribution function seaborn的displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。
seaborn的displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。
import scipy.stats as st
y = Train_data['price']
plt.figure(1);plt.title('Johnson SU')
sns.distplot(y,kde=False,fit=st.johnsonsu) # kde=False关闭核密度分布,rug表示在x轴上每个观测上生成的小细条(边际毛毯)
step 2: 查看偏度和峰度
sns.distplot(Train_data['price']) # 单个变量y
print("Skewness: %f" % Train_data['price'].skew())
print("Kurtosis: %f" % Train_data['price'].kurt())
查看所有变量
Train_data.skew(),Train_data.kurt()
# 偏度的频率图
sns.distplot(Train_data.skew(),color='blue',axlabel='Skewness')
sns.distplot(Train_data.kurt(),color = 'orange', axlabel = 'Kurtness')
step 3: 预测值的具体频数
Notes
如果大于某数的值极少,可以把这些当作特殊值(异常值) 直接删除或者填充plt.hist(Train_data['price'],orientation = 'vertical',histtype = 'bar', color = 'red')
plt.show()
Notes:
price:一般用 Log 变换plt.hist(np.log(Train_data['price']),
orientation='vertical',
histtype = 'bar',
color = 'red')
plt.show()
6. 特征 features
特征分为类别特征和数字特征,并对类别特征查看unique分布
for cat_fea in categorical_features:
print(cat_fea + "的特征分布如下")
print("{}的特征有{}个不同的值".format(cat_fea,Train_data[cat_fea].nunique()))
print(Train_data[cat_fea].value_counts())
7. 数字特征分布
相关性分析(热力图)
查看几个特征的偏度和峰度
每个数字特征的分布可视化
数字特征相互之间的关系可视化 (pairs() in R?)
多变量互相回归关系可视化
step 1: 相关性分析
numeric_features.append('price')
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
print(correlation['price'].sort_values(ascending = False),'\n')
Heatmap
f,ax = plt.subplots(figsize = (7,7))
plt.title('Correlation of Numeric Features with Price',y=1,size =16)
sns.heatmap(correlation,square = True,vmax = 0.8)
del price_numeric['price']
step 2: 查看几个特征的偏度和峰值
for col in numeric_features:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(Train_data[col].skew()),
' ',
'Kurtosis: {:06.2f}'.format(Train_data[col].kurt()))
step 3: 每个数字特征的分布可视化
Notes:
melt: 列名被转换为一列叫做’variable’的普通列,而所有的值变成了‘value’列 FacetGrid: 一个绘制多个图表(以网格形式显示)的接口f = pd.melt(Train_data,value_vars = numeric_features)
g = sns.FacetGrid(f,col="variable",col_wrap=2, sharex =False, sharey = False)
g = g.map(sns.distplot,"value")
step 4 : 数字特征相互之间的关系 可视化
Notes:
sns.pairplot() 的参数及其用法 kind:用于控制非对角线上的图的类型,可选"scatter"与"reg" 非对角线上的散点图拟合出一条回归直线,更直观地显示变量之间的关系 diag_kind:控制对角线上的图的类型,可选"hist"与"kde" hue :针对某一字段进行分类,不同类别的点会以不同的颜色显现出来 markers:控制散点的样式 markers=["+", “s”, “D”] 当我们想单独研究某两个(或多个)变量的关系时,我们只需要通过vars参数指定你想研究的变量 vars, x_vars, y_vars:选择数据中的特定字段,以list形式传入sns.set()
columns = ['price', 'v_12', 'v_8' , 'v_0', 'power', 'v_5', 'v_2', 'v_6', 'v_1', 'v_14']
sns.pairplot(Train_data[columns],size = 2,kind='scatter',diag_kind='kde')
plt.show()
step 5: 多变量互相回归关系 可视化
fig, ((ax1, ax2), (ax3, ax4), (ax5, ax6), (ax7, ax8), (ax9, ax10)) = plt.subplots(nrows=5, ncols=2, figsize=(24, 20))
v_12_scatter_plot = pd.concat([Y_train,Train_data['v_12']],axis=1)
sns.regplot(x='v_12',y='price',data = v_12_scatter_plot,scatter=True,fit_reg=True,ax=ax1)
v_8_scatter_plot = pd.concat([Y_train,Train_data['v_8']],axis = 1)
sns.regplot(x='v_8',y = 'price',data = v_8_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
v_0_scatter_plot = pd.concat([Y_train,Train_data['v_0']],axis = 1)
sns.regplot(x='v_0',y = 'price',data = v_0_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
power_scatter_plot = pd.concat([Y_train,Train_data['power']],axis = 1)
sns.regplot(x='power',y = 'price',data = power_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
v_5_scatter_plot = pd.concat([Y_train,Train_data['v_5']],axis = 1)
sns.regplot(x='v_5',y = 'price',data = v_5_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
v_2_scatter_plot = pd.concat([Y_train,Train_data['v_2']],axis = 1)
sns.regplot(x='v_2',y = 'price',data = v_2_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
v_6_scatter_plot = pd.concat([Y_train,Train_data['v_6']],axis = 1)
sns.regplot(x='v_6',y = 'price',data = v_6_scatter_plot,scatter= True, fit_reg=True, ax=ax7)
v_1_scatter_plot = pd.concat([Y_train,Train_data['v_1']],axis = 1)
sns.regplot(x='v_1',y = 'price',data = v_1_scatter_plot,scatter= True, fit_reg=True, ax=ax8)
v_14_scatter_plot = pd.concat([Y_train,Train_data['v_14']],axis = 1)
sns.regplot(x='v_14',y = 'price',data = v_14_scatter_plot,scatter= True, fit_reg=True, ax=ax9)
v_13_scatter_plot = pd.concat([Y_train,Train_data['v_13']],axis = 1)
sns.regplot(x='v_13',y = 'price',data = v_13_scatter_plot,scatter= True, fit_reg=True, ax=ax10)
8. 类型特征分析
unique分布
类别特征箱型图可视化
类别特征的小提琴可视化
类别特征的柱形图可视化类别
特征的每个类别频数可视化(count_plot)
step 1: unique 分布
for fea in categorical_features:
print(Train_data[fea].nunique())
step 2: 类别特征 箱型图可视化
Notes:
arr.astype(’category‘): 转换数据类型 转化到类别特征 xticks() 返回了两个对象,一个是刻标(locs),另一个是刻度标签 locs, labels = xticks() xticks() 还可以传入matplotlib.text。Text类的属性来控制显示的样式categorical_features = ['model',
'brand',
'bodyType',
'fuelType',
'gearbox',
'notRepairedDamage']
for c in categorical_features:
Train_data[c] = Train_data[c].astype('category')
if Train_data[c].isnull().any():
Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
Train_data[c] = Train_data[c].fillna('MISSING')
def boxplot(x,y,**kwargs):
sns.boxplot(x=x, y=y)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data,id_vars = ['price'],value_vars=categorical_features)
g = sns.FacetGrid(f,col="variable",col_wrap=2,sharex=False, sharey=False,size=5)
g = g.map(boxplot,"value","price")
step 3: 类别特征的小提琴可视化
Notes:
violinplot与boxplot扮演类似的角色, 它显示了定量数据在一个(或多个)分类变量的多个层次上的分布,这些分布可以进行比较。 不像箱形图中所有绘图组件都对应于实际数据点,小提琴绘图以基础分布的核密度估计为特征。catg_list = categorical_features
target = 'price'
for catg in catg_list:
sns.violinplot(x=catg,y=target,data=Train_data)
plt.show()
step 4: 类别特征的柱形图可视化
Notes:
*args 可变参数: 是一些入参的元组,表示任何多个无名参数,它是一个tuple kwargs就是传入的多个键值对key = value参数。关键字参数,它是一个dict 同时使用args和**kwargs时,必须args参数列要在**kwargs前,像foo(a=1, b=‘2’, c=3, a’, 1, None, )这样调用的话,会提示语法错误plt.style.use("ggplot")
def bar_plot(x,y,**kwargs):
sns.barplot(x=x,y=y)
x=plt.xticks(rotation = 90)
f = pd.melt(Train_data,id_vars=['price'],value_vars=categorical_features)
g = sns.FacetGrid(f,col="variable",col_wrap=2,sharex=False,sharey=False,size=5)
g = g.map(bar_plot,"value","price")
step 5:类别特征的每个类型 频数可视化
plt.style.use("ggplot")
def count_plot(x,**kwargs):
sns.countplot(x=x)
x=plt.xticks(rotation=90)
f = pd.melt(Train_data,value_vars=categorical_features)
g = sns.FacetGrid(f,col="variable",col_wrap=2,sharex=False,sharey=False,size=5)
g = g.map(count_plot,"value")
9. 用Pandas_profiling生成数据报告
用pandas_profiling生成一个较为全面的可视化和数据报告(较为简单、方便) 最终打开html文件即可
import pandas_profiling
pfr = pandas_profiling.ProfileReport(Train_data)
pfr.to_file("./example.html")
作者:Scarlett_can