面试题36. 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
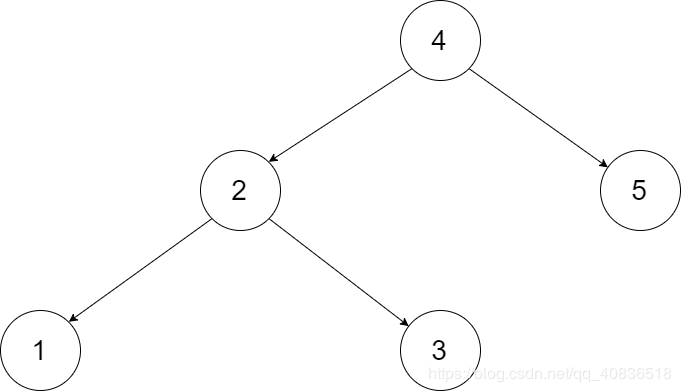
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
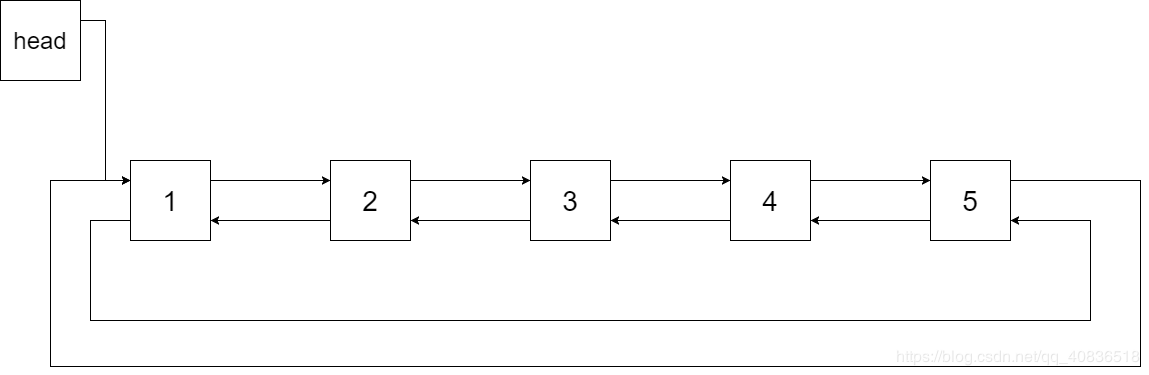
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
分析:
由于这个题目已经是二叉搜索树,所以转换成有序的链表很容易,对于当前节点来说,它的前驱一定是它左子树最右边的节点,它的后继一定是它的右子树最左边的节点。发现这一点后,会发现其实这就是中序遍历的顺序嘛,于是只需要稍稍修改中序遍历的代码即可。
基本思路是分别用pre_node, node表示上一次访问的节点和当前访问节点,则pre_node.right=node, node.left=pre_node。但是如何得到上一次遍历访问的节点,到底是用递归还是用栈的实现方式呢?
递归写起来简单,但是我没想到怎么记录上次访问的节点,于是一开始我选择在中序遍历栈的写法上修改。中序遍历栈的写法可参见我之前的博客https://blog.csdn.net/qq_40836518/article/details/104895412。
法一:
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
if root==None:
return None
stack=[]
node=root
first_node=None
pre_node=None
while stack or node:
while node:
stack.append(node)
node=node.left
node=stack.pop()
if pre_node!=None:
pre_node.right=node
node.left=pre_node
else:
first_node=node
pre_node=node
node=node.right
first_node.left=pre_node
pre_node.right=first_node
return first_node
后来看了看剑指offer书上的解法,方法和我的差不多,只不过用递归实现的,用全局变量来表示pre_node。一直以来我比较抵触在递归里面修改全局变量,因为一般情况下会导致每次递归时全局变量变得面目全非,把自己给绕进去了。不过,由于二叉树递归调用的顺序还是很清楚的,因此在这里用一个pre_node全局变量也还是可以分析清楚它的变化的。
法二:
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def recursive(self, node):
if node==None:
return
self.recursive(node.left)
if self.pre_node!=None:
self.pre_node.right=node
node.left=self.pre_node
else:
self.first_node=node
self.pre_node=node
self.recursive(node.right)
def treeToDoublyList(self, root: 'Node') -> 'Node':
if root==None:
return None
self.pre_node=None
self.first_node=None
self.recursive(root)
self.first_node.left=self.pre_node
self.pre_node.right=self.first_node
return self.first_node
会中序遍历之后so easy~~
作者:xk-wang