搜索进阶之迭代加深搜索
首先这个不要怕这个东西,其实我刚开始学这个搜索也觉得特别高大上,觉得都是很高大上让人听不懂的专业术语,其实说白了迭代加深搜索的思想和精髓就是控制了搜索深度的dfs,但是却能够达到广搜的效果。它的搜索状态无穷多种,深度可以是无限深,宽度也可以是无限宽。当你采用深搜时会超时,当你采用广搜时队列会螺旋爆炸,这时就需要上迭代加深。
比如有这样一类题让你在这类题里面找到最小的解就可以。(通常情况下迭代加深搜索的题都是有解,只是解的大小问题),怎么样写这个呢?其实就是深搜控制了深度,搜索历程就是先搜索深度为1的所有情况,看看能不能达到最终目标,如果能达到最终目标,结束搜索。如果不能继续增加可以搜索的深度,但是前面所有的搜索的结果不会被保存,下一次深度加1继续从头开始搜虽然看起来好像干了很多重复的事情,其实不是的,当你搜索第k的深度的时候,前面k-1深度的所有情况都不值得一提。这也就是为什么迭代加深不会像广搜一样超出内存,如果超了内存你来打我~~并且时间上并不比广搜慢太多。
应用场景1.当你拿到题发现时间很充足,并且内存可能无法满足你搜索时拓展出的n多状态。
2.题目一般情况下有解并且可能有多个解让你求出最优的解。
3.想用就用吧~~
经典例题迭代加深入门第一题------埃及分数
埃及分数,没有题目连接但是是一个很经典的迭代加深搜索的例子,题目要求就是给定一个分数让你把这个分数拆成若干个分数相加的和,并且这些分数的分子都是1。分数个数尽量少,而且最小的分数尽量大,也就是最小的那个分数的分母越小越好,典型的迭代加深搜索的例子。
最后就是注意剪枝很重要,ai >= b(maxd-d+1)的含义:a/b >= (maxd-d+1)/i;为啥这样判断?因为我们知道分数的分母是越来越大的,在当前这个深度分母最小都是i,后面分母越来越大,不可能都是i,所以,如果假设当前深度之后的每一步分母都是i,也需要maxd-d+1个相同的分子,很显然这样的情况不存在。因为分母越来越大,分数越来越小就算你后面所有分数的极限值都是1/i,全部加起来也不过是(maxd-d+1)/i,如果当前分数剩余的分数值都大于等于这个放缩的极限值那么这个深度肯定没有解。
//注意换long long,乘积的时候防止爆炸
#include
#include
#include
#include
#include
using namespace std;
#define ll long long
ll s[100],v[100];
ll gcd(ll a,ll b) //gcd约分缩小运算数
{
while(b){
ll t = a%b;
a = b;
b = t;
}
return a;
}
bool better(int d) //与之前的比较结果做比较
{
for(int i = d;i >= 0;i--){
if(s[i] != v[i]){
if(s[i] == -1 || s[i] > v[i]){ //判断当前的v是不是比之前的s更优
return true; //从后面判断更直观,因为前面很多分母都是相同的,后面往前判断更快
}
else{
return false;
}
}
}
return false;
}
bool iddfs(int d,int maxd,ll from,ll a,ll b)
{
if(d == maxd){ //达到最大深度
if(b%a){ //最后一个分数a/b不能约分成分子为1的情况
return false;
}
v[d] = b/a;
if(better(d)){
memcpy(s,v,sizeof(ll)*(d+1)); //拷贝d+1个分数分母,等价于下面的循环
// for(int i = 0;i = b*(maxd-d+1)){ // a/b >= (maxd-d+1)/i;
break; //很重要的一个剪枝技巧用了数学的放缩法
}
v[d] = i;
ll na = a*i - b; //新的分子
ll nb = b*i; //新的分母
ll g = gcd(na,nb); //最大公约数,尽量约分,以便缩小a,b的范围,防止超出
if(iddfs(d+1,maxd,i+1,na/g,nb/g)){
flag = true;
}
}
return flag;
}
int main()
{
freopen("C:\\Users\\Administrator\\Desktop\\input.txt","r",stdin);
freopen("C:\\Users\\Administrator\\Desktop\\output2.txt","w",stdout);
int a,b;
while(cin>>a>>b){
memset(v,0,sizeof(v));
int d;
for(d = 1;d 100){ //无解,我拍了400组数据没有一组无解。。。。
printf("No solution.\n");
}
else{
printf("%d/%d = ",a,b);
for(int i = 0;i < d;i++){
printf("1/%lld+",s[i]);
}
printf("1/%lld.\n",s[d]);
}
}
return 0;
}
迭代加深入门第二题------骑士精神
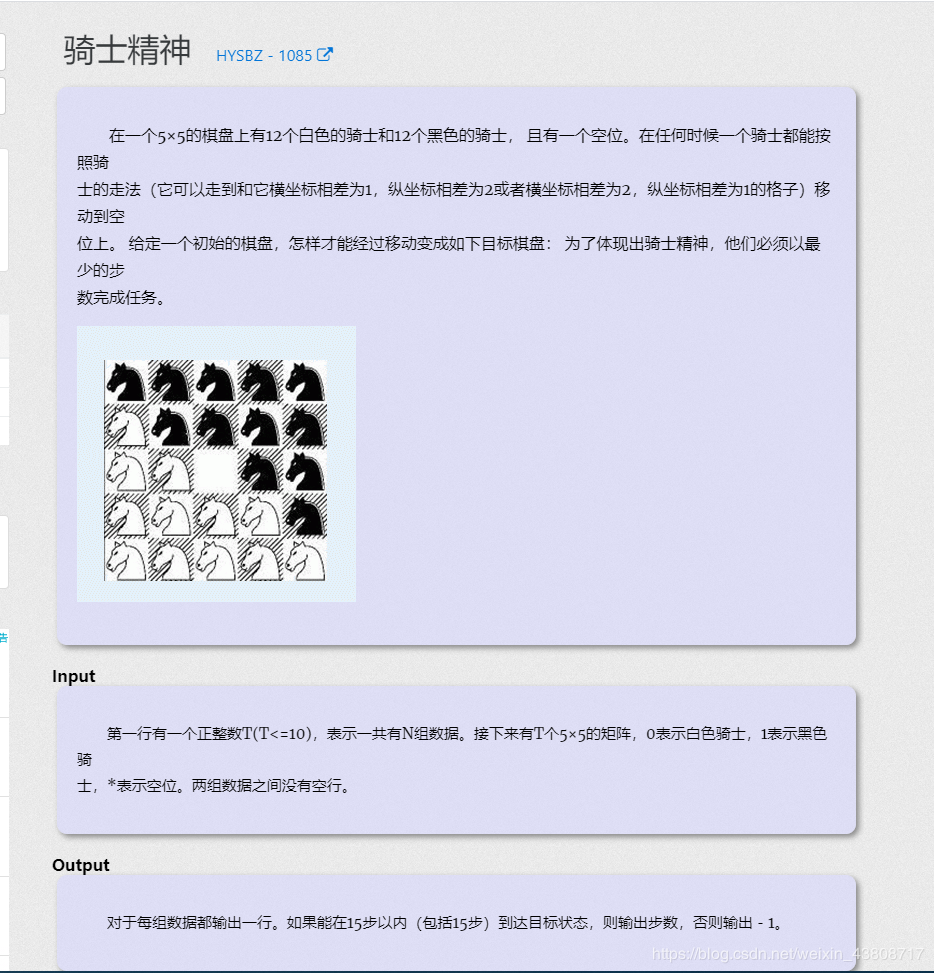
题目大意就是给你一个5*5的棋盘问你最多15步之内能不能抵达给定的状态。如果能够抵达那么最小的步数是多少,如果不能抵达输出-1。很明显的迭代加深搜索题,搭配估计函数做一点预期估计。如果上来直接不控制深度,肯定超时,毕竟dfs那么笨他哪知道什么时候停下来转弯不是?所以我们用迭代加深控制它,得出来的结果即是最优跑起来又最快,题目可以去VJ上找。
#include
#include
#include
#include
using namespace std;
int goal[5][5] = {{1,1,1,1,1},{0,1,1,1,1},
{0,0,2,1,1},{0,0,0,0,1},{0,0,0,0,0}};
int map[5][5];
int dx[] = {2,2,-2,-2,1,1,-1,-1};
int dy[] = {1,-1,1,-1,2,-2,2,-2};
int h() //计算与预期棋盘不相同棋子的个数
{
int cnt = 0;
for(int i = 0;i < 5;i++){
for(int j = 0;j maxd){ //进行估计
return false; //当前搜索的次数与估价的次数和是否能够在达到最大深度之前得出答案
}
for(int i = 0;i < 8;i++){
int nx = x + dx[i];
int ny = y + dy[i];
if(nx 4 || ny 4){
continue;
}
swap(map[x][y],map[nx][ny]);
if(iddfs(d+1,maxd,nx,ny)){
return true;
}
swap(map[x][y],map[nx][ny]);
}
return false;
}
int main()
{
int t;
scanf("%d",&t);
while(t--){
int sx,sy,d;
for(int i = 0;i < 5;i++){
char s[10];
scanf("%s",s);
for(int j = 0;j < 5;j++){
if(s[j] == '1' || s[j] == '0'){
map[i][j] = s[j] - '0';
}
if(s[j] == '*'){
map[i][j] = 2;
sx = i;sy = j;
}
}
}
for(d = 1;d 15){
printf("-1\n");
}
else{
printf("%d\n",d);
}
}
return 0;
}
迭代加深入门第三题------次方问题

POJ3134
就是给一个数n,问从x^1开始怎么 样最快算到x^n,可以利用中间的计算结果进行乘除运算,实则就是上面的指数进行加减运算。所以问题就缩减为1------n怎么样通过利用中间运算获得的答案进行加法或者减法运算快速得到n。并且要求输出最小的运算次数,很显然无论怎么样都有解,只是解的大小问题,最大次数没有上限,最小次数却又下限。采用迭代加深思想深度越小先搜到的肯定是最小答案。
乐观估计:当前剩余拓展的深度次数maxd-d的差值假设是m,意味着还可以拓展m次,就算m次运算都是针对当前的值进行翻倍运算,最大也就是使当前这个数x翻了2^m,如果这样都比n小那么没有必要在算下去,这个深度下该x算不到答案。
#include
#include
#include
#include
#include
using namespace std;
int n,s[1005];
bool iddfs(int d,int maxd,int x)
{
if(d > maxd || (x*(1<<(maxd-d)) < n)){ //超出最大深度和乐观估计
return false;
}
if(x == n){ //拓展到节点结束搜索
return true;
}
s[d] = x;
for(int i = 0;i <= d;i++){ //拓展所有的情况
if(iddfs(d+1,maxd,x+s[i])){ //所有的加法情况
return true;
}
if(iddfs(d+1,maxd,fabs(x-s[i]))){
return true; //所有的减法情况,记得加绝对值不允许出现指数是负数的情况
}
}
return false; //搜不到答案
}
int main()
{
while(~scanf("%d",&n) && n){
int i;
for(i = 0; true ;i++){
memset(s,0,sizeof(s));
if(iddfs(0,i,1)){
break;
}
}
printf("%d\n",i);
}
return 0;
}
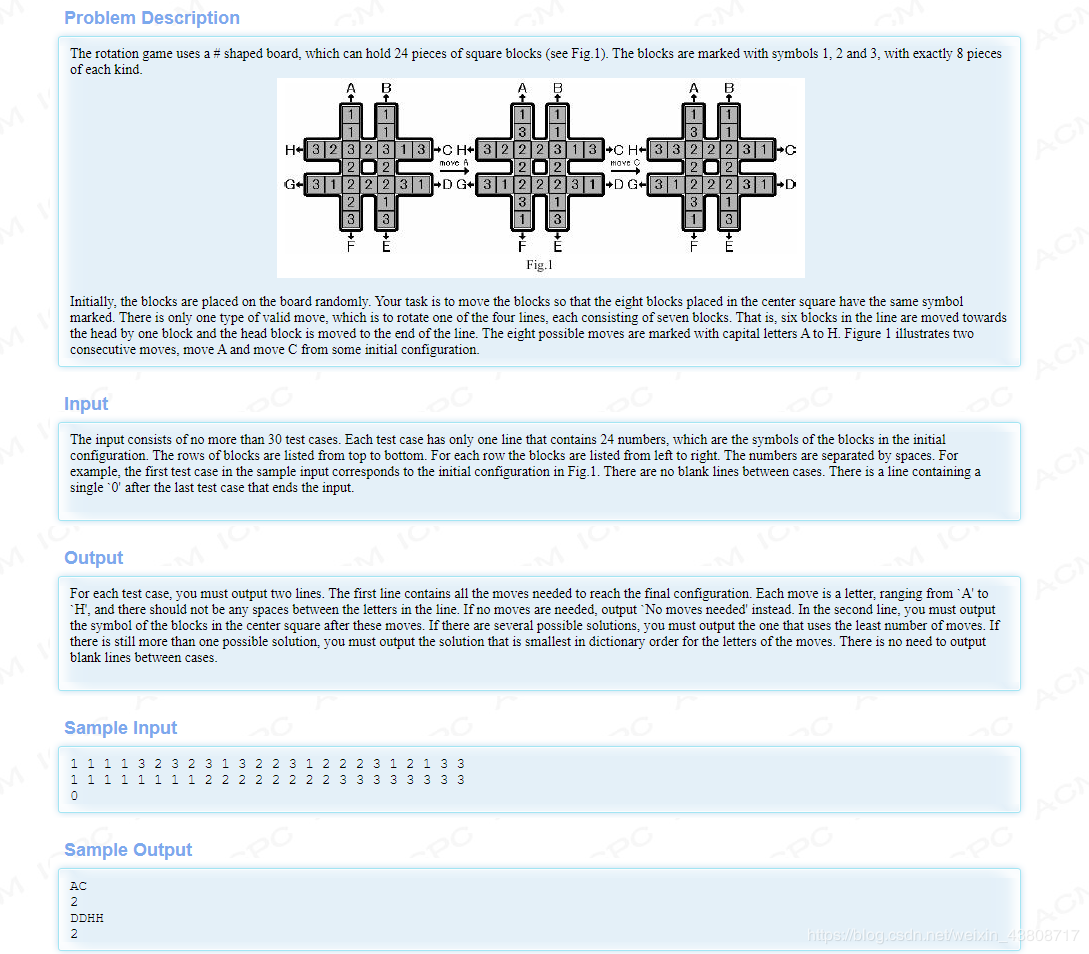
迭代加深入门第四题------旋转游戏
题目传送门HDU1667
题目大意就是ABCDEFGH八种操作,每次只能进行一种操作,问最小多少步能够使得中间的8块同为1或者2或者3。迭代加深搜索思想 + 剪枝技巧
#include
#include
#include
#include
#include
#include
using namespace std;
int s[8][7] = {
{0,2,6,11,15,20,22}, //A
{1,3,8,12,17,21,23}, //B
{10,9,8,7,6,5,4}, //C
{19,18,17,16,15,14,13}, //D
{23,21,17,12,8,3,1}, //E
{22,20,15,11,6,2,0}, //F
{13,14,15,16,17,18,19}, //G
{4,5,6,7,8,9,10}, //H
};
int center[] = {6,7,8,11,12,15,16,17}; //中心8个位置的坐标
int ans[] = {5,4,7,6,1,0,3,2,-1}; //反向回溯对应的操作
int map[25]; //数字图
char way[105]; //操作方法
int get_h() //乐观估计
{ //找出中间8个位置1,2,3最多的那一个的数目
int cnt[4] = {0};
int num = -1;
for(int i = 0;i < 8;i++){
cnt[map[center[i]]]++;
num = max(num,cnt[map[center[i]]]);
}
return 8 - num;
}
int get_move(int k) //移动
{
int t = map[s[k][0]];
for(int i = 0;i maxd || get_h() + d > maxd){ //超出最大允许深度或者估计之后无解
return false;
}
if(get_h() == 0){ //到达目标状态
way[d] = '\0';
printf("%s\n%d\n",way,map[6]);
return true;
}
for(int i = 0;i < 8;i++){ //八种情况拓展
if(ans[i] != k){ //当前搜索和上一次搜索不互逆,小优化~
way[d] = 'A' + i;
get_move(i); //正向移动
if(iddfs(d+1,maxd,i)){
return true;
}
get_move(ans[i]); //反向移回
}
}
return false;
}
int main()
{
int n;
while(~scanf("%d",&n) && n){
map[0] = n;
for(int i = 1;i < 24;i++){
scanf("%d",&map[i]);
}
if(get_h() == 0){ //给的状态直接上目标状态
printf("No moves needed\n%d\n",map[6]);
continue;
}
for(int i = 1; true ;i++){
if(iddfs(0,i,8)){
break;
}
}
}
return 0;
}
作者:薯条割脉