机器学习 | 使用TensorFlow搭建神经网络实现鸢尾花分类
鸢尾花分类问题是机器学习领域一个非常经典的问题,本文将利用神经网络来实现鸢尾花分类
实验环境:Windows10、TensorFlow2.0、Spyder
参考资料:人工智能实践:TensorFlow笔记第一讲
1、鸢尾花分类问题描述根据鸢尾花的花萼、花瓣的长度和宽度可以将鸢尾花分成三个品种

我们可以使用以下代码读取鸢尾花数据集
from sklearn.datasets import load_iris
x_data = load_iris().data
y_data = load_iris().target
该数据集含有150个样本,每个样本由四个特征和一个标签组成,四个特征分别为:
花萼长度 花萼宽度 花瓣长度 花瓣宽度标签值为:
| 标签值 | 0 | 1 | 2 |
|---|---|---|---|
| 鸢尾花品种 | 山鸢尾 | 变色鸢尾 | 维吉尼亚鸢尾 |
本文搭建的神经网络由一个输入层(包含4个输入节点)、一个输出层(包含3个输出节点)组成。
神经网络单个神经元的结构如下
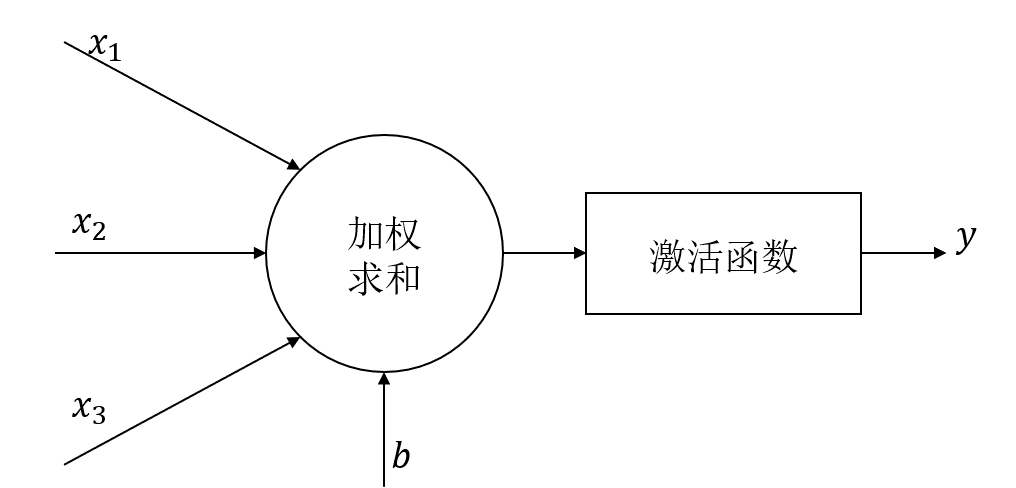
本方法略去了激活函数,直接将加权结果作为输出,加权公式为:
y=x∗w+b
y=x*w+b
y=x∗w+b
其中xxx为1×41\times 41×4矩阵,yyy为1×31\times 31×3矩阵,www为4×34\times 34×3的矩阵,bbb为1×31\times 31×3矩阵
用来描述预测值yyy与真实标签y.‾y\underline{.}y.的差距,本文方法使用均方误差来描述损失函数。
MSE(y,y.‾)=∑k=0n(y−y.‾)2n
MSE(y,y\underline{.})=\frac{\sum_{k=0}^n(y-y\underline{.})^2}{n}
MSE(y,y.)=n∑k=0n(y−y.)2
为了找到一组参数www和bbb使损失函数最小,本文使用梯度下降法进行参数优化
梯度下降法:沿损失函数梯度下降的方向,寻找损失函数的最小值,得到最优参数的方法。
梯度下降法即对损失函数中的各个参量求偏导,得到的结果即为损失函数梯度下降的方向。公式如下
wt+1=wt−lr⋅∂loss∂wtbt+1=bt−lr⋅∂loss∂btwt+1⋅x+bt+1→y
w_{t+1}=w_t-lr\cdot \frac{\partial loss}{\partial w_t}\\
b_{t+1}=b_t-lr\cdot \frac{\partial loss}{\partial b_t}\\
w_{t+1}\cdot x+b_{t+1}\to y
wt+1=wt−lr⋅∂wt∂lossbt+1=bt−lr⋅∂bt∂losswt+1⋅x+bt+1→y
其中lrlrlr表示学习率,不同的学习率会对参数更新造成不同的影响,如学习率过小,会造成参数更新过慢;学习率过大,会造成损失函数震荡。
完整程序如下:
# -*- coding: utf-8 -*-
"""
Created on Thu Apr 9 11:01:13 2020
@author: 白鸟无言
"""
# 鸢尾花分类
import tensorflow as tf
import numpy as np
from matplotlib import pyplot as plt
# 读入数据集
from sklearn.datasets import load_iris
x_data = load_iris().data
y_data = load_iris().target
# 打乱数据集
np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
# 选择倒数第30之前的数据作为训练集
x_train = x_data[:-30]
y_train = y_data[:-30]
# 选择倒数第30之后的数据作为测试集
x_test = x_data[-30:]
y_test = y_data[-30:]
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# 分批处理
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 随机初始化待更新的参数
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1))
lr = 0.2 # 学习率/步长
epoch = 300 # 迭代总次数
loss_all = 0 # 每次迭代的损失
loss_list = [] # 存储每一次迭代的损失
acc_list = [] # 存储每一次迭代结果的准确率
for epoch in range(epoch):
# 训练
# 更新权重
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape:
# 前向传播得到当前权值下的推理结果 y = x * w1 + b1
y = tf.matmul(x_train, w1) + b1;
# 使用softmax将推理结果转换到[0, 1]之间
y = tf.nn.softmax(y)
# 将标签转换为独热码,即0:0 0 1, 1:0 1 0, 2:1 0 0
y_ = tf.one_hot(y_train, depth=3)
# 求均方误差
loss = tf.reduce_mean(tf.square(y_ - y))
loss_all += loss.numpy()
# 分别对损失函数的w1、b1求偏导
grads = tape.gradient(loss, [w1, b1])
# 更新w1、b1 w1 = w1 - lr * w1_grad b1 = b1 - lr * b1_grad
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
# 打印此次迭代的损失
print("Ecoph:{}, Loss:{}".format(epoch, loss_all / 4))
loss_list.append(loss_all / 4)
loss_all = 0
# 测试
# 计算此次迭代结果的正确率
# 在真实训练时可以略过,这里只是为了画出正确率曲线
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 前向传播得到当前权值下的推理结果 y = x * w1 + b1
y = tf.matmul(x_test, w1) + b1
# 使用softmax将预测结果转换到[0, 1]之间
y = tf.nn.softmax(y)
# 找到最大值的索引
pred = tf.argmax(y, axis=1)
pred = tf.cast(pred, dtype=y_test.dtype)
# 将预测结果与真实标签对比
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
correct = tf.reduce_sum(correct)
total_correct += int(correct)
total_number += x_test.shape[0]
acc = total_correct / total_number
acc_list.append(acc)
print("Acc:", acc)
print("-------------------")
# 画出损失函数曲线
plt.plot(loss_list)
plt.title("Loss Curve")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
# 画出正确率曲线
plt.plot(acc_list)
plt.title("Acc Curve")
plt.xlabel("Epoch")
plt.ylabel("Acc")
plt.show()
4、运行结果
损失函数曲线如下,可以看到损失函数随着迭代次数的增加逐渐减小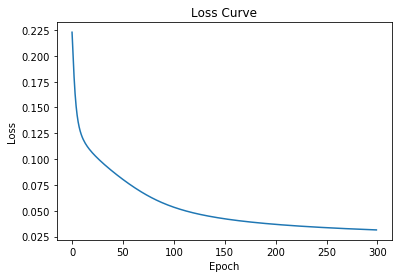 正确率曲线
正确率曲线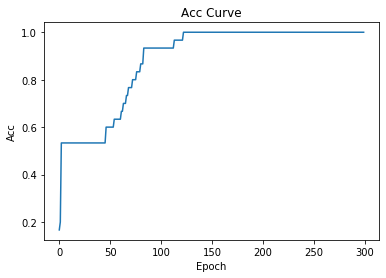
如有谬误,敬请指正!
作者:白鸟无言