最优化理论实践——神经网络训练
用了一周的时间学习了一下最优化理论这门课,为了更深度地理解各种优化方法的理念和算法过程,自己把这些算法应用到实践中是很必要的。为此我设计了和优化算法相关的四个实验项目,在这里和大家分享一下。
无约束优化方法





根据链式法则,从输出层直接对误差函数求导得到的误差(这里我们简写为δ),就可以通过和上面的这些局部导数不断做乘积、并把新的δ传播到上一层,就能计算得到所有参数的导数。通过一阶导数,就能实现基本的梯度优化方法。

神经网络可以很好地处理函数拟合问题,因为模型带有大量可调节的参数,而且内置了非线性的激励函数,这就让神经网络实现各种函数的拟合成为可能。
前面已经说到,全连接神经网络(前馈神经网络)的前向传播和反向传播都可以写成简单的矩阵与矩阵相乘,矩阵和常数相乘,矩阵和常数相加的形式。只要按照上面的公式实现矩阵运算,就可以搭建一个自己的神经网络了。
我们这里将要实现的是函数拟合,训练的过程可以理解为是让神经网络输出与真实函数值相差最小的过程,因此使用均方误差MSE进行训练。
均方误差是二次型函数,显然是凸函数。神经网络内的参数w和b都没有约束条件,即训练神经网络的问题是一个无约束凸优化问题。
算法的选择是要经过考虑的。首先,神经网络内参数的导数容易从反向传播算法得到,但是二阶导数不是那么容易计算,因此我们不使用牛顿法。最速下降法的最优步长确定过程要多次计算函数值来保证下降的最速性,但是神经网络的一次运算就涉及到大量的矩阵运算,用最速下降来计算是得不偿失的。
因此,可以考虑的方法有固定步长的最速下降法(梯度下降法),以及基于修正公式的共轭梯度法。这里使用梯度下降法训练一个二输入,一输出的三层神经网络,拟合函数y=sin(x_1)cos(x_2)。
为了高效执行矩阵运算,使用MATLAB实现。
%设计一个三层的神经网络,用于近似goal函数
%输入层:2->8
%隐藏层:8->4
%输出层:4->1
%参数需要随机初始化
Win = randn(8,2);
Bin = zeros(8,1);
Whid = randn(4,8);
Bhid = zeros(4,1);
Wout = randn(1,4);
Bout = zeros(1,1);
lr = 0.05;%学习率
g = @goal;
err = 0;
for iter=1:1000000
%生成随机数据的输入x用于训练,我们想拟合一个周期内的goal
xin = rand(2,1)*2*pi';
x = Win*xin;
x = x+Bin;
x = sigmoid(x);
yin = x;
xhid = x;%隐藏层输入
x = Whid*x;
x = x+Bhid;
x = sigmoid(x);
yhid = x;
xout = x;%输出层输入
x = Wout*x;
x = x+Bout;
%x = sigmoid(x);
yout = x;
%正向传播
delta = Error(g,xin,yout);
err = err+abs(delta);
if mod(iter,1000)==0
fprintf('Iteration: %d\n',iter);
fprintf('Error: %f\n',err/1000);
err = 0;
end
%delta = delta.*yout.*(1-yout);
Bout = Bout-lr*delta;
dw = delta*xout';
Wout = Wout-lr*dw;
delta = Wout'*delta;
%
delta = delta.*yhid.*(1-yhid);
Bhid = Bhid-lr*delta;
dw = delta*xhid';
Whid = Whid-lr*dw;
delta = Whid'*delta;
%
delta = delta.*yin.*(1-yin);
Bin = Bin-lr*delta;
dw = delta*xin';
Win = Win-lr*dw;
%反向传播
end
[X,Y] = meshgrid(0:0.1:2*pi,0:0.1:2*pi);
Z = X;
for i=1:63
for j=1:63
x = [X(i,j),Y(i,j)]';
x = sigmoid(Win*x+Bin);
x = sigmoid(Whid*x+Bhid);
x = sigmoid(Wout*x+Bout);
Z(i,j) = x;
end
end
surf(X,Y,Z);
title('Output of neural network');
最终的误差和神经网络输出的函数图像如下
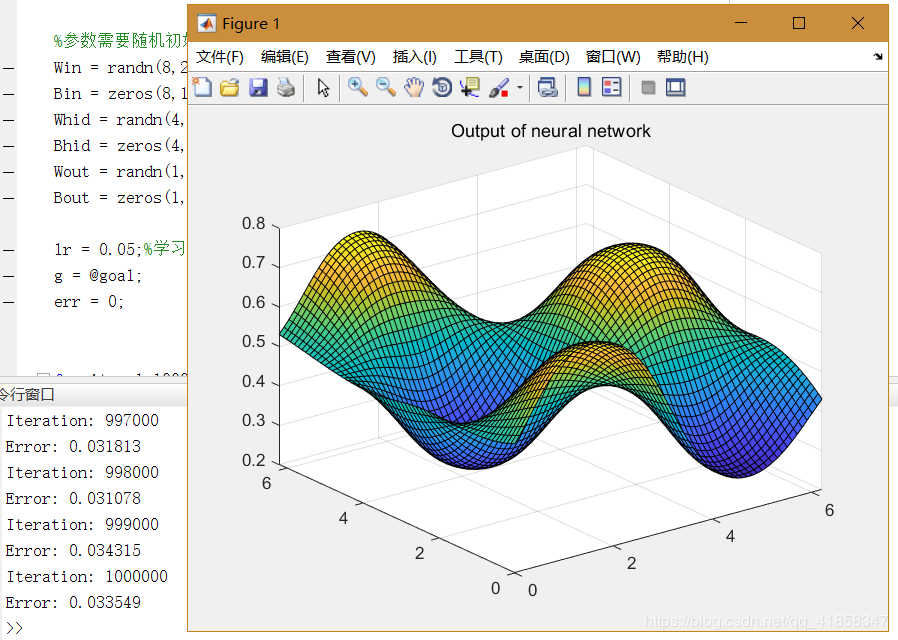
在进行了优化理论的学习后,一些原本看起来复杂基础的机器学习理论都变得浅显易懂。有人说机器学习的基石就是概率论和优化理论,看来并不无道理。
博客中图片及代码为本人自制,转载请声明。
作者:Hαlcyon