【神经网络】{3} ——计算复杂的非线性假设模型(1)(学习笔记)
此处通过例子来展示神经网络是怎样计算复杂的非线性假设模型的。
例子:
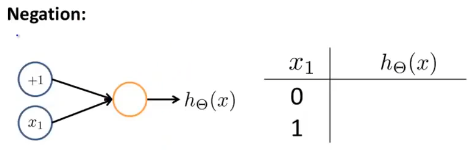
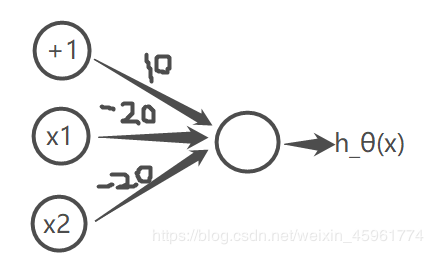
这个网络只有一个输入特征x_1,还有一个偏置单元+1。现在用权重(参数),也就是+10和-20把这些单元连接起来:
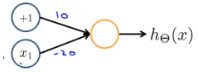
故假设模型为:
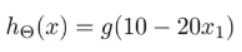
故:

观察得出的结果,会发现它确实实现了函数NOT x_1。
若要实现逻辑非运算,大体思想就是在预期得到非结果的变量前面放一个很大的负权重(参数)。比如说-20乘以x_1,这就是对x_1做逻辑非运算的主要思路。
那么如何计算这个方程呢?
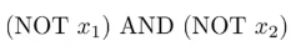
通过上面的例子,我们可以知道其中一个方法就是在x_1和x_2前面放一个较大负数作为权值(参数)。
不过还有一个方法,就是建立只有一个输出单元的神经网络来计算结果。
如图所示:
这样,我们就建立了一个小规模的神经网络来计算这个逻辑函数。

现在把这3块单独的部分组合到网络当中,把这三部分组合在一起来计算x_1 XNOR x_2。
首先把网络画出来,取这3个输入单元+1、x_1和x_2,来建立第一个隐藏单元,因为是第一个隐藏单元,所以把它称为a^(2)_1。
接下来把用红线表示的关于x_1和x_2的神经网络的权值(参数)都照着写下来:
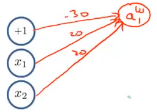
接下来建立第二个隐藏单元,把它称为a^(2)_2,表示第二层的第二个隐藏单元。
然后将中间青线表示的网络的权值照搬下来:
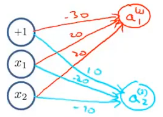
现在列出这个网络的真值表:
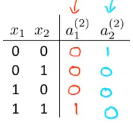
最后建立输出单元a^(3)_1,它将会输出h(x)。
然后把计算OR函数的神经网络照搬下来,这里需要一个偏置单元+1,然后把绿色网络的权值都复制过来:
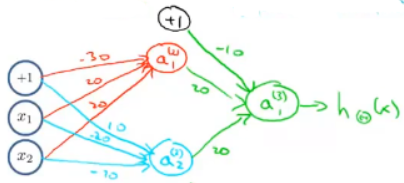
我们已经知道,它计算的是OR函数,我们继续列出它的真值表:
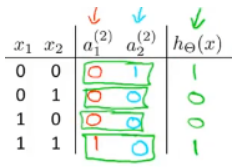
所以,当x_1和x_2同时为0或同时为1时,h(x)就等于1。在坐标系打叉的位置上,h(x)将会输出1,而在打圈的位置上会输出0:
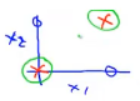
因此这个神经网络有一个输入层、一个隐藏层和一个输出层,最后会得到一个非线性的决策边界,用以计算XNOR函数。
更通俗的解释是:我们的输入都放在输入层,然后在中间放一个隐藏层,用来计算一些关于输入的略微复杂的功能,然后再继续增加一层,用以计算一个更复杂非线性函数。
这就是为什么神经网络可以计算这种复杂的函数。
当网络拥有许多层:
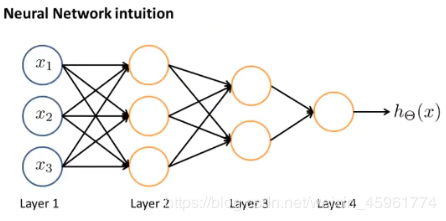
在第二层中有一些关于输入的相对简单的函数,第三层又在此基础上计算更加复杂的方程,再往后一层,计算的函数越来越复杂。
例如在识别手写数字的神经网络结构中,你所输入的图像,或者说原始的像素点,通过第一个隐藏层,计算出一系列特征,再通过下一个隐藏层,计算出更复杂的特征,然后再往下再复杂,最后这些特征被用于逻辑回归分类器的最后一层,来准确地预测出神经网络所看到的数字。
这个例子能够使我们对神经网络所学习的这些复杂的函数有一个直观的理解。
参考资料:吴恩达机器学习系列课程
作者:Giyn