《动手学深度学习》梯度爆炸、梯度消失、过拟合、欠拟合
深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸(explosion)。
当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个层数为LLL的多层感知机的第lll层H(l)\boldsymbol{H}^{(l)}H(l)的权重参数为W(l)\boldsymbol{W}^{(l)}W(l),输出层H(L)\boldsymbol{H}^{(L)}H(L)的权重参数为W(L)\boldsymbol{W}^{(L)}W(L)。为了便于讨论,不考虑偏差参数,且设所有隐藏层的激活函数为恒等映射(identity mapping)ϕ(x)=x\phi(x) = xϕ(x)=x。给定输入X\boldsymbol{X}X,多层感知机的第lll层的输出H(l)=XW(1)W(2)…W(l)\boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)}H(l)=XW(1)W(2)…W(l)。此时,如果层数lll较大,H(l)\boldsymbol{H}^{(l)}H(l)的计算可能会出现衰减或爆炸。举个例子,假设输入和所有层的权重参数都是标量,如权重参数为0.2和5,多层感知机的第30层输出为输入X\boldsymbol{X}X分别与0.230≈1×10−210.2^{30} \approx 1 \times 10^{-21}0.230≈1×10−21(消失)和530≈9×10205^{30} \approx 9 \times 10^{20}530≈9×1020(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
过拟合和欠拟合模型训练中经常出现的两类典型问题:
一类是模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting); 另一类是模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。在实践中,我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题,在这里我们重点讨论两个因素:模型复杂度和训练数据集大小。

权重衰减等价于 L2L_2L2 范数正则化(regularization)。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。
ℓ(w1,w2,b)+λ2n∣w∣2,
\ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2,
ℓ(w1,w2,b)+2nλ∣w∣2,
def l2_penalty(w):
return (w**2).sum() / 2
# 添加了L2范数惩罚项的损失计算
# 超参数 lambd,lambd为0时惩罚项不起作用
l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
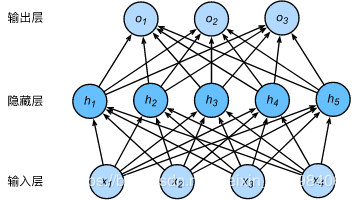
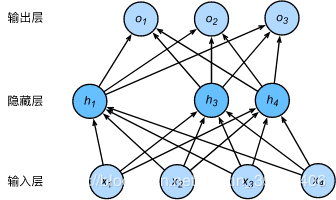
丢弃法
随机清零隐藏层的值,在训练模型时起到正则化的作用
丢弃后
def dropout(X, drop_prob):
X = X.float()
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return torch.zeros_like(X)
mask = (torch.rand(X.shape) < keep_prob).float()
return mask * X / keep_prob
def net(X, is_training=True):
X = X.view(-1, num_inputs)
H1 = (torch.matmul(X, W1) + b1).relu()
if is_training: # 只在训练模型时使用丢弃法
H1 = dropout(H1, drop_prob1) # 在第一层全连接后添加丢弃层
H2 = (torch.matmul(H1, W2) + b2).relu()
if is_training:
H2 = dropout(H2, drop_prob2) # 在第二层全连接后添加丢弃层
return torch.matmul(H2, W3) + b3
作者:Nick_Spider