吴恩达深度学习:第二课,第二周:优化算法
首先需要将数据集取为子集Mini-batch,然后进行训练
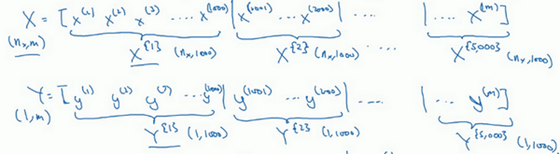
引入了大括号t来代表不同的mini-batch,所以我们有X{t}X^{\{t\}}X{t}和Y{t}Y^{\{t\}}Y{t}。
维度方面:如果X{1}X^{\{1\}}X{1}是一个有1000个样本的训练集,或者说是1000个样本的xxx值,所以维数应该是(nx,1000)(n_x,1000)(nx,1000),X{2}X^{\{2\}}X{2}的维数应该是(n_x,1000)。而这些(Y{t})(Y^{\{t\}})(Y{t})的维数都是(1,1000)。
前向传播因为我们有5000个各有1000个样本的组,在for循环里你要做得基本就是对X{t}X^{\{t\}}X{t}和Y{t}Y^{\{t\}}Y{t}执行一步梯度下降法。

由图片得,计算Z,然后是A,直到计算出预测A[L]A^{[L]}A[L],最后计算带正则项的代价函数。
J=11000∑i=1lL(J(i),y(i))+λ21000∑l∥w[l]∥F2
J=\frac{1}{1000} \sum_{i=1}^{l} L\left(\mathcal{J}^{(i)}, y^{(i)}\right)+\frac{\lambda}{21000} \sum_{l}\left\|w^{[l]}\right\|_{F}^{2}
J=10001i=1∑lL(J(i),y(i))+21000λl∑∥∥∥w[l]∥∥∥F2
写下来的代码就是1代(1 epoch)的训练。一代这个词意味着只是一次遍历了训练集。
梯度下降法如出一辙,除了你现在的对象不是X,Y,而是X{t}X^{\{t\}}X{t}和Y{t}Y^{\{t\}}Y{t}。接下来,你执行反向传播来计算J{t}J^{\{t\}}J{t}的梯度。
理解mini-batch 梯度下降法不同优化算法的代价函数:
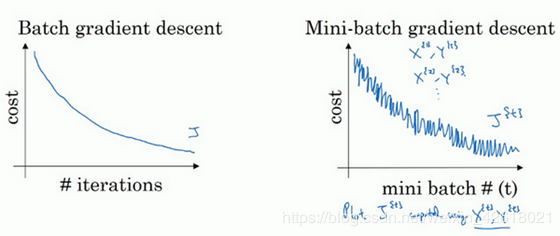
梯度下降:正常下降
随机梯度下降:上下波动,有噪声,最终波动在最小点附近
假设mini-batch大小为1,就有了新的算法,叫做随机梯度下降法,每个样本都是独立的mini-batch,当你看第一个mini-batch,也就是X({1})和Y({1}),如果mini-batch大小为1,它就是你的第一个训练样本,这就是你的第一个训练样本。接着再看第二个mini-batch,也就是第二个训练样本,采取梯度下降步骤,然后是第三个训练样本,以此类推,一次只处理一个。
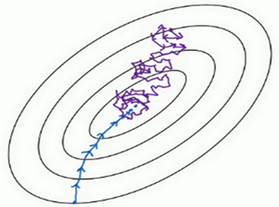
每次迭代,你只对一个样本进行梯度下降,大部分时候你向着全局最小值靠近,有时候你会远离最小值,因为那个样本恰好给你指的方向不对,因此随机梯度下降法是有很多噪声的,平均来看,它最终会靠近最小值,不过有时候也会方向错误,因为随机梯度下降法永远不会收敛,而是会一直在最小值附近波动,但它并不会在达到最小值并停留在此。 全部样本
你会失去所有向量化带给你的加速,因为一次性只处理了一个训练样本,这样效率过于低下
无法得到比较小的误差:改变学习率可以有效降低噪声
合理的簇大小首先,如果训练集较小,直接使用batch梯度下降法,样本集较小就没必要使用mini-batch梯度下降法,你可以快速处理整个训练集,所以使用batch梯度下降法也很好,这里的少是说小于2000个样本,这样比较适合使用batch梯度下降法。不然,样本数目较大的话,一般的mini-batch大小为64到512,考虑到电脑内存设置和使用的方式,如果mini-batch大小是2的n次方,代码会运行地快一些,64就是2的6次方,以此类推,128是2的7次方,256是2的8次方,512是2的9次方。所以我经常把mini-batch大小设成2的次方。在上一个视频里,我的mini-batch大小设为了1000,建议你可以试一下1024,也就是2的10次方。也有mini-batch的大小为1024,不过比较少见,64到512的mini-batch比较常见。
指数加权平均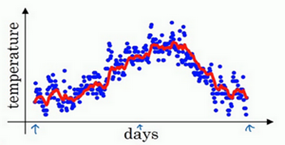
公式:
vt=βvt−1+(1−β)θt
v_{t}=\beta v_{t-1}+(1-\beta) \theta_{t}
vt=βvt−1+(1−β)θt
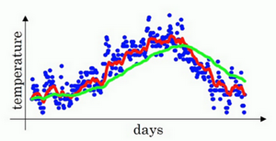
作用:依赖前面天数的平均,使当前的值v趋于平滑稳定。
描述β\betaβ参数意义:
公式拆分过程:
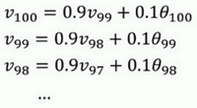
如果把这些公式合并:
v100=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+0.1×(0.9)4θ96+⋯
v_{100}=0.1 \theta_{100}+0.1 \times 0.9 \theta_{99}+0.1 \times(0.9)^{2} \theta_{98}+0.1 \times(0.9)^{3} \theta_{97}+0.1 \times(0.9)^{4} \theta_{96}+\cdots
v100=0.1θ100+0.1×0.9θ99+0.1×(0.9)2θ98+0.1×(0.9)3θ97+0.1×(0.9)4θ96+⋯
解析:
所以这是一个加和并平均,100号数据,也就是当日温度。我们分析v100v_{100}v100的组成,也就是在一年第100天计算的数据,但是这个是总和,包括100号数据,99号数据,97号数据等等。画图的一个办法是,假设我们有一些日期的温度,所以这是数据,这是t,所以100号数据有个数值,99号数据有个数值,98号数据等等,t为100,99,98等等,这就是数日的温度数值。
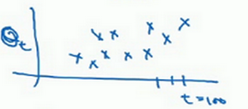
构建一个指数衰减函数,从0.10.10.1开始,到0.1×0.90.1×0.90.1×0.9,到0.1×(0.9)20.1×(0.9)^20.1×(0.9)2,以此类推,所以就有了这个指数衰减函数。

当权重=0.9时,10天后,曲线的高度下降到1/3,相当于在峰值的1/e。换句话说10天前的温度对今日影响已经是越来越少。
出现问题:按照公式,前面几天的向量v,会远小于当天的温度。
计算移动平均数的时候,初始化v0=0,v1=0.98v0+0.02θ1v_0=0,v_1=0.98v_0+0.02θ_1v0=0,v1=0.98v0+0.02θ1,但是v0=0v_0=0v0=0,所以这部分没有了(0.98v0)(0.98v_0)(0.98v0),所以v1=0.02θ1v_1=0.02θ_1v1=0.02θ1,所以如果一天温度是40华氏度,那么v1=0.02θ1=0.02×40=8v_1=0.02θ_1=0.02×40=8v1=0.02θ1=0.02×40=8,因此得到的值会小很多,所以第一天温度的估测不准!
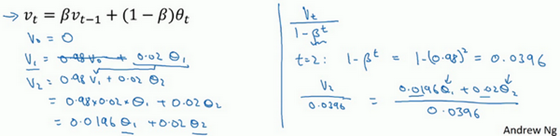
偏差修正公式:
vt1−βt
\frac{v_{t}}{1-\beta^{t}}
1−βtvt
此时随着t的越来越大,下面的分母趋近于1,而且前面估计偏少的参数也会得到修正。
动量梯度下降法 优化成本函数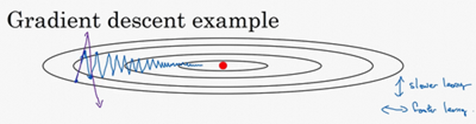
为了减少摆动,加快横移,使用指数加权平均
公式:


dw代表水平,db代表竖直方向的摆动。使用该算法,加快了水平速度,减少了摆动大小
SdW=βSdW+(1−β)dW2−>small
S_{d W}=\beta S_{d W}+(1-\beta) d W^{2} ->small
SdW=βSdW+(1−β)dW2−>small
Sdb=βSdb+(1−β)db2−>big
S_{d b}=\beta S_{d b}+(1-\beta) d b^{2} ->big
Sdb=βSdb+(1−β)db2−>big
W:=W−adWSdW,b:=b−αdbSdb
W:=W-a \frac{d W}{\sqrt{S_{d W}}}, b:=b-\alpha \frac{d b}{\sqrt{S_{d b}}}
W:=W−aSdWdW,b:=b−αSdbdb
因为本身摆动就大,其中的dW偏少,db偏大。这就导致了更新项的W变化更大,b变化更小
细节:不能让SwS_wSw等于0,在平方根的分母加上ϵ\epsilonϵ。
与Momentum很像但是,还多了在水平上加速的能力。
Adam 优化算法将Momentum与RMSprop算法柔和一起。
算法公式:

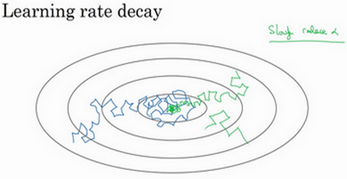
但要慢慢减少学习率a的话,在初期的时候,a学习率还较大,你的学习还是相对较快,但随着a变小,你的步伐也会变慢变小,所以最后你的曲线(绿色线)会在最小值附近的一小块区域里摆动,而不是在训练过程中,大幅度在最小值附近摆动。
所以慢慢减少a的本质在于,在学习初期,你能承受较大的步伐,但当开始收敛的时候,小一些的学习率能让你步伐小一些。
a=11+decayrate∗ epoch −numa0
a=\frac{1}{1+d e c a y r a t e * \text { epoch }-\mathrm{num}} a_{0}
a=1+decayrate∗ epoch −num1a0
其他的衰减学习率方法
指数衰减:a=0.95epoch - num a0a=0.95^{\text {epoch - num }} a_{0}a=0.95epoch - num a0 a=kta0a=\frac{k}{\sqrt{t}} a_{0}a=tka0 局部最优的问题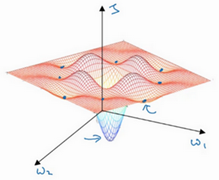
人们发出局部最优所认为的二维平面,但是我们实际的神经网络是高维曲面,如下:
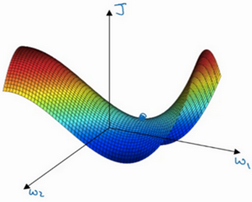
它存在鞍点,也就是最优点,存在平稳段,会使学习在平稳段变得缓慢
作者:于大大想要去旅行