算法——Horner scheme

Gaia ·

更新时间:2024-11-10

· 957 次阅读

题目描述

In numerical analysis, the Horner scheme or Horner algorithm, named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner’s method describes a manual process by which one may approximate the roots of a polynomial equation. The Horner scheme can also be viewed as a fast algorithm for dividing a polynomial by a linear polynomial with Ruffini’s rule.
Application
The Horner scheme is often used to convert between different positional numeral systems — in which case x is the base of the number system, and the ai coefficients are the digits of the base-x representation of a given number — and can also be used if x is a matrix, in which case the gain in computational efficiency is even greater.
History
Even though the algorithm is named after William George Horner, who described it in 1819, the method was already known to Isaac Newton in 1669, and even earlier to the Chinese mathematician Ch’in Chiu-Shao in the 13th century. TASK: write a program to calculate sum of Polynomial by Horner scheme.

输入

tow lines. The first line have tow numbers,n and x, n<=20, x<=10 The second line have n+1 numbers, a0,a1…an.

输出

The sum of Polynomial

样例输入

5 2
0 1 2 3 4 5

样例输出

258

代码

#include
using namespace std;
int main(){
	int n, x, sum = 0;
	cin>>n>>x;
	int a[20];
	for(int i = 0; i >a[i];
	} 
	for(int i = n; i >= 0; i--){
		sum = sum*x + a[i];
	}
	cout<<sum<<endl;
	return 0;
}

思路

1.Horner 算法是以英国数学家 William George Horner 命名的一种多项式求值的快速算法，同秦九韶算法：
只需要n次乘法和n次加法。在人工计算时，一次大大简化了运算过程。
2.
把一个n次多项式

改写成如下形式：
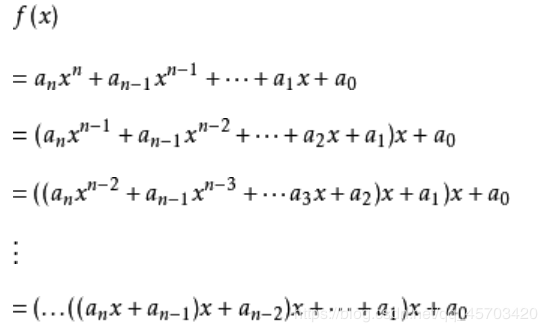
在这里插入图片描述
3.求多项式的值时，首先计算最内层括号内一次多项式的值。
4.对于一个n次多项式，至多做n次乘法和n次加法。