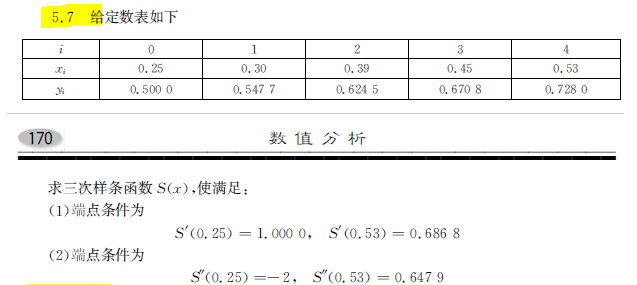
三次样条插值 简单例子 曲线拟合 BIT数值分析5.7
题目
部分思路见注释
代码
# 三次样条插值
import sympy as sp
# x = [-3, -1, 0, 3, 4]
# y = [7, 11, 26, 56, 29]
x = [0.25, 0.30, 0.39, 0.45, 0.53]
y = [0.5000, 0.5477, 0.6245, 0.6708, 0.7280]
lenx = len(x)
num = [i for i in range(lenx)]
h = [None]
lamda = [None] * lenx
miu = [None] * lenx
d = [None] * lenx
M = []
ans = [['*' for i in range(lenx)] for i in range(lenx)]
ans[0] = ["*", "x**3系数", "2次方系数", "1次方系数", "常数项"]
# for j in range(lenx):
# print(ans[j])
# 存放差商
cs1 = []
cs2 = []
cs3 = []
csetc = []
def save( l , y ):
if (l == 1 and y not in cs1):
cs1.append(y)
elif (l == 2 and y not in cs2):
cs2.append(y)
elif (l == 3 and y not in cs3):
cs3.append(y)
elif (y not in csetc):
csetc.append(y)
def chsh(n):
lenn = len(n)
# print('------', lenn, '-----,n:',n)
try:
if( lenn n)
for i in range(1, lenx):
ans[i][0] = "S"+ str(i) + "(x) "
ans[i][1] = ( M[i] - M[i-1] ) / ( 6 * h[i])
ans[i][2] = - ( M[i] * x[i-1] - M[i-1] * x[i] ) / (2 * h[i])
ans[i][3] = ( ( M[i] * x[i-1]**2 - M[i-1] * x[i]**2 ) / 2*h[i] \
- ( y[i-1] / h[i] - M[i-1] * h[i] / 6 ) \
+ ( y[i] /h[i] - M[i] * h[i] / 6 ))
ans[i][4] = (M[i-1] * x[i]**3 - M[i] * x[i-1]**3) / ( 6 * h[i]) \
+ ( y[i-1] /h[i] - M[i-1] * h[i] / 6 ) * x[i] \
- ( y[i] / h[i] - M[i] * h[i] /6) * x[i-1]
for j in range(lenx):
print(ans[j])
def main():
while(True):
try:
global mode
mode = eval(input("选择端点条件类型:1 二阶导数 2 一阶导数 --------"))
# 端点条件,自然样条也需要输入0
global dy0, dyn
dy0, dyn = eval(input("输入两端导数值dy0,dyn(用,分开):"))
print(f" dy0 = {dy0}, dyn = {dyn}")
# 准备 求差商表,存到二阶就行
print("准备 求差商表,存到二阶就行")
chsh(num)
print("--1阶", cs1)
print("--2阶", cs2)
# print("--3阶", cs3)
# print("--3+阶", csetc)
print(" 1&2 计算h、d、lamda、miu")
# 优先计算h,d和lamda、miu在后面
# 1 计算h
cal_h()
# 2 计算d、lamda、miu
cal_lamda_miu()
cal_d()
print(" hi:", h)
print(" λi: ", lamda)
print(" μi: ", miu)
print(" di: ", d)
# 3 解n-1阶三对角方程组,带入端点条件计算M0,Mn,
# 端点条件2:
# d[0] = ((y[1] - y[0]) / h[1] - dy0) * 6 / h[1]
# d[lenx - 1] = (dyn - (y[-1] - y[-2]) / h[-1]) * 6 / h[-1]
# miun=lamda0=1,带入方程组计算
print(" 3 计算M")
cal_M()
# 4 后面带入求 Si(x),i:1->n 怎么整?
# 想了一下还是只有把公式先化成多项式再求,吧嗒吧嗒两页草稿纸算出来多项式的系数(也不知道对不对)
print(" 4 带入求 Si(x),i:1->n")
cal_ans()
except Exception as err:
print(err)
main()
# x=list(enumerate(['one','two','three']))
# print(x)
# import sympy as sp
# x,y = sp.symbols("x,y")
# a = sp.solve([x+y-0.2,x+3*y-1],[x,y])
# print(a)
'''
全局变量可以直接在函数体内容部使用的,你可以直接访问,但是注意的是,如果对于不可变类型的数据,如果在函数里面进行了赋值操作,
则对外面的全局变量不产生影响,因为相当于新建了一个局部变量,只是名字和全局一样,而对于可变类型,如果使用赋值语句,同样对外部
不产生影响,但是使用方法的话就会对外部产生影响
如果使用的是赋值语句,在函数内部相当于新建了一个变量,并且重新给了指向,但是有时候我们想把这个变量就是外部的那个全局变量,在
赋值操作的时候,就是对全局变量给了重新的指向,这个时候可以通过global关键字表示我在函数里面的这个变量是使用的全局那个。
来源:https://blog.csdn.net/qq_28888837/article/details/88060376
'''
运行结果
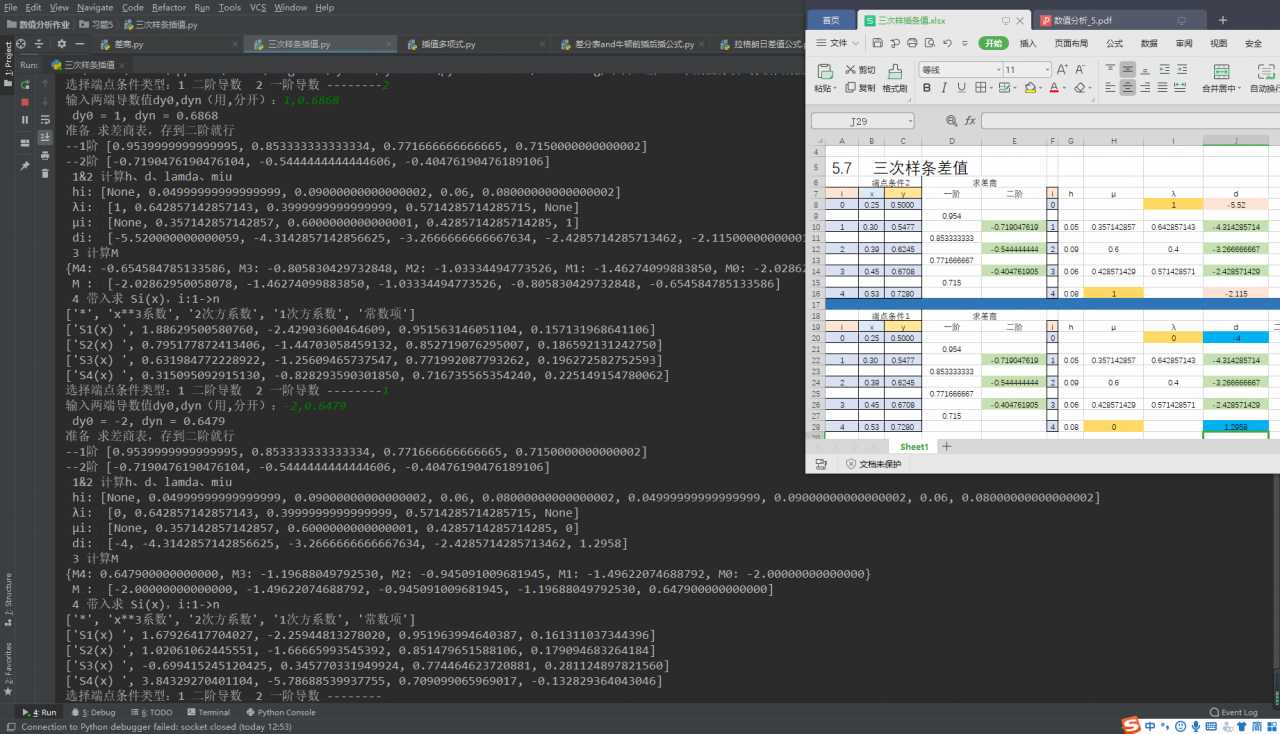
多项式计算出错,致代码有误,已更正
作者:peterlong0612