奇异值分解（Singular Value Decomposition，SVD）
Am×n=UΣVTUUT=ImVVT=InΣ=diag(σ1,σ2,...,σp)σ1≥σ2≥...≥σp≥0p=min(m,n)A_{m \times n} = U \Sigma V^T\\ UU^T=I_m\\ VV^T=I_n\\ \Sigma=diag(\sigma_1,\sigma_2,...,\sigma_p) \\ \sigma_1\ge \sigma_2 \ge...\ge\sigma_p \ge0\\ p=\min(m,n)Am×n=UΣVTUUT=ImVVT=InΣ=diag(σ1,σ2,...,σp)σ1≥σ2≥...≥σp≥0p=min(m,n)
UΣVTU \Sigma V^TUΣVT 称为矩阵 AAA 的奇异值分解（SVD），UUU 是 mmm 阶正交矩阵， VVV 是 nnn 阶正交矩阵，Σ\SigmaΣ 是 m×nm \times nm×n 的对角矩阵 σi\sigma_iσi 称为矩阵 AAA 的奇异值 UUU 的列向量，左奇异向量 VVV 的列向量，右奇异向量 1.2 两种形式 1.2.1 紧奇异值分解上面的SVD称为：完全SVD
Am×n=UrΣrVrTA_{m \times n} = U_r \Sigma_r V_r^TAm×n=UrΣrVrT
紧奇异值分解，仅由前 rrr 列得到，对角矩阵 Σr\Sigma_rΣr 的秩与原始矩阵 AAA 的秩相等
只取最大的 k 个奇异值 (k<r,r为矩阵的秩)(k < r, r 为矩阵的秩)(k<r,r为矩阵的秩) 对应的部分，就得到矩阵的截断奇异值分解
实际应用中提到的，经常指的截断SVD
Am×n≈UkΣkVkT,0<k<Rank(A)A_{m \times n} \approx U_k \Sigma_k V_k^T,\quad 0<k<Rank(A)Am×n≈UkΣkVkT,0<k<Rank(A)
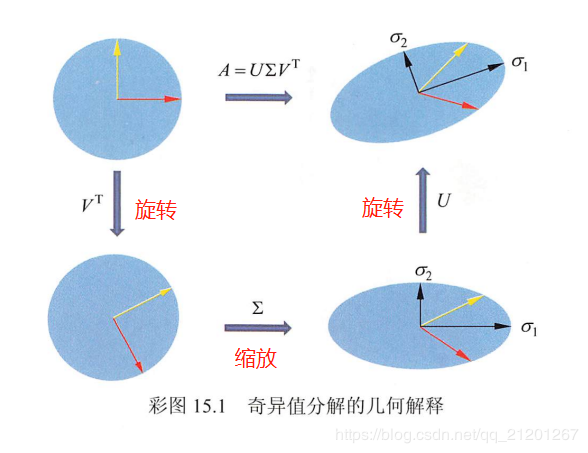
在实际应用中，常常需要对矩阵的数据进行压缩，将其近似表示，奇异值分解提供了一种方法 奇异值分解是在平方损失（弗罗贝尼乌斯范数）意义下对矩阵的最优近似 紧奇异值分解—>无损压缩 截断奇异值分解—>有损压缩 1.3 几何解释矩阵的SVD也可以看作是将其 对应的线性变换 分解为 旋转变换、缩放变换及旋转变换的组合。
这个变换的组合一定存在。
ATA=(UΣVT)T(UΣVT)=V(ΣTΣ)VTAAT=(UΣVT)(UΣVT)T=U(ΣΣT)UTA^TA=(U\Sigma V^T)^T(U\Sigma V^T)=V(\Sigma^T\Sigma)V^T\\
AA^T=(U\Sigma V^T)(U\Sigma V^T)^T=U(\Sigma\Sigma^T)U^TATA=(UΣVT)T(UΣVT)=V(ΣTΣ)VTAAT=(UΣVT)(UΣVT)T=U(ΣΣT)UT
对称矩阵 ATAA^TAATA 和 AATAA^TAAT 的特征分解 可由矩阵 AAA 的奇异值分解矩阵表示
(2)
AV=UΣ⇒Avj=σjuj,j=1,2,...,nATU=VΣT⇒ATuj=σjvj,j=1,2,...,n;ATuj=0,j=n+1,n+2,...,mAV=U\Sigma \Rightarrow Av_j=\sigma_ju_j,j=1,2,...,n\\
A^TU=V\Sigma^T \Rightarrow A^Tu_j=\sigma_jv_j,j=1,2,...,n;A^Tu_j=0,j=n+1,n+2,...,mAV=UΣ⇒Avj=σjuj,j=1,2,...,nATU=VΣT⇒ATuj=σjvj,j=1,2,...,n;ATuj=0,j=n+1,n+2,...,m
(3) SVD奇异值 σ1,σ1,...,σn\sigma_1,\sigma_1,...,\sigma_nσ1,σ1,...,σn 是唯一的，但矩阵 U,VU,VU,V 不唯一
(4) 矩阵 AAA 和 Σ\SigmaΣ 的秩相等，等于正奇异值 σi\sigma_iσi 的个数 rrr
(5) 矩阵 AAA 的 rrr 个右奇异向量 v1,v2,...,vrv_1,v_2,...,v_rv1,v2,...,vr 构成 ATA^TAT 的值域 的一组标准正交基；
矩阵 AAA 的 n−rn-rn−r 个右奇异向量 vr+1,vr+2,...,vnv_r+1,v_r+2,...,v_nvr+1,vr+2,...,vn 构成 AAA 的零空间 的一组标准正交基；
矩阵 AAA 的 rrr 个左奇异向量 u1,u2,...,uru_1,u_2,...,u_ru1,u2,...,ur 构成 AAA 的值域 的一组标准正交基；
矩阵 AAA 的 m−rm-rm−r 个左奇异向量 ur+1,ur+2,...,umu_r+1,u_r+2,...,u_mur+1,ur+2,...,um 构成 ATA^TAT 的零空间 的一组标准正交基
奇异值分解也是一种矩阵近似的方法，这个近似是在弗罗贝尼乌斯范数（Frobenius norm）意义下的近似
矩阵的弗罗贝尼乌斯范数是 向量的L2范数的直接推广，对应着机器学习中的平方损失函数
设矩阵 A=[aij]m×nA=[a_{ij}]_{m \times n}A=[aij]m×n, 其弗罗贝尼乌斯范数为：∣∣A∣∣F=(∑i=1m∑j=1n(aij)2)1/2||A||_F = \bigg( \sum\limits_{i=1}^m \sum\limits_{j=1}^n(a_{ij})^2\bigg)^{1/2}∣∣A∣∣F=(i=1∑mj=1∑n(aij)2)1/2
假设 AAA 的奇异值分解为 A=UΣVTA=U\Sigma V^TA=UΣVT ，其中对角矩阵 Σ=diag(σ1,σ2,...,σp)\Sigma=diag(\sigma_1,\sigma_2,...,\sigma_p)Σ=diag(σ1,σ2,...,σp)，则 ∣∣A∣∣F=(σ12+σ22+...+σn2)1/2||A||_F = \bigg(\sigma_1^2+\sigma_2^2+...+\sigma_n^2\bigg)^{1/2}∣∣A∣∣F=(σ12+σ22+...+σn2)1/2
2.2 矩阵的最优近似奇异值分解 是在平方损失（弗罗贝尼乌斯范数）意义下对矩阵的最优近似，即数据压缩
弗罗贝尼乌斯范数意义下的无损压缩
截断奇异值分解：是有损压缩。截断奇异值分解得到的矩阵的秩为k，通常远小于原始矩阵的秩r，所以是由低秩矩阵实现了对原始矩阵的压缩
2.3 矩阵的外积展开式
矩阵 AAA 的奇异值分解 UΣVTU\Sigma V^TUΣVT 也可以由外积形式表示
将 AAA 的奇异值分解看成矩阵 UΣU\SigmaUΣ 和 VTV^TVT 的乘积，将 UΣU\SigmaUΣ 按列向量分块，将 VTV^TVT 按行向量分块，即得
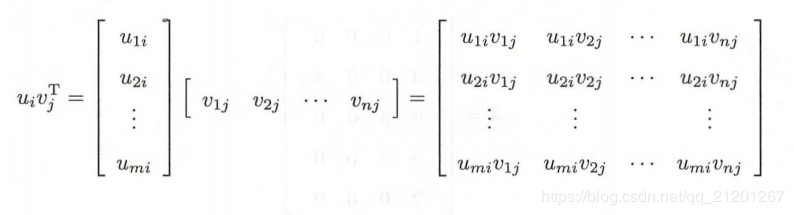3. 奇异值分解Python计算
import numpy as np
a = np.random.randint(-10,10,(4, 3)).astype(float)
print(a)
print("-----------------")
u, sigma, vT = np.linalg.svd(a)
print(u)
print("-----------------")
print(sigma)
print("-----------------")
print(vT)
print("-----------------")
# 将sigma 转成矩阵
SigmaMat = np.zeros((4,3))
SigmaMat[:3, :3] = np.diag(sigma)
print(SigmaMat)
print("------验证-------")
a_ = np.dot(u, np.dot(SigmaMat, vT))
print(a_)
结果：
[[-6. 8. 9.]
[ 6. 8. -8.]
[ 6. -1. 2.]
[ 6. 9. -9.]]
-----------------
[[-0.30430452 0.93673281 0.17295875 -0.00395842]
[ 0.64134399 0.19762952 0.04109474 -0.74022408]
[ 0.06410812 -0.16033168 0.98267774 0.0672931 ]
[ 0.70140345 0.24034966 -0.05235412 0.66897256]]
-----------------
[19.56867211 12.83046891 6.0370638 ]
-----------------
[[ 0.52466311 0.45709993 -0.71818401]
[-0.30821258 0.88838353 0.34026417]
[ 0.79355758 0.04282928 0.60698602]]
-----------------
[[19.56867211 0. 0. ]
[ 0. 12.83046891 0. ]
[ 0. 0. 6.0370638 ]
[ 0. 0. 0. ]]
------验证-------
[[-6. 8. 9.]
[ 6. 8. -8.]
[ 6. -1. 2.]
[ 6. 9. -9.]]
作者：Michael阿明
