机器学习(MACHINE LEARNING) 【周志华版-”西瓜书“-笔记】 DAY16-强化学习
当前的机器学习算法可以分为3种:有监督的学习(Supervised Learning)、无监督的学习(Unsupervised Learning)和强化学习(Reinforcement Learning),结构图如下所示:
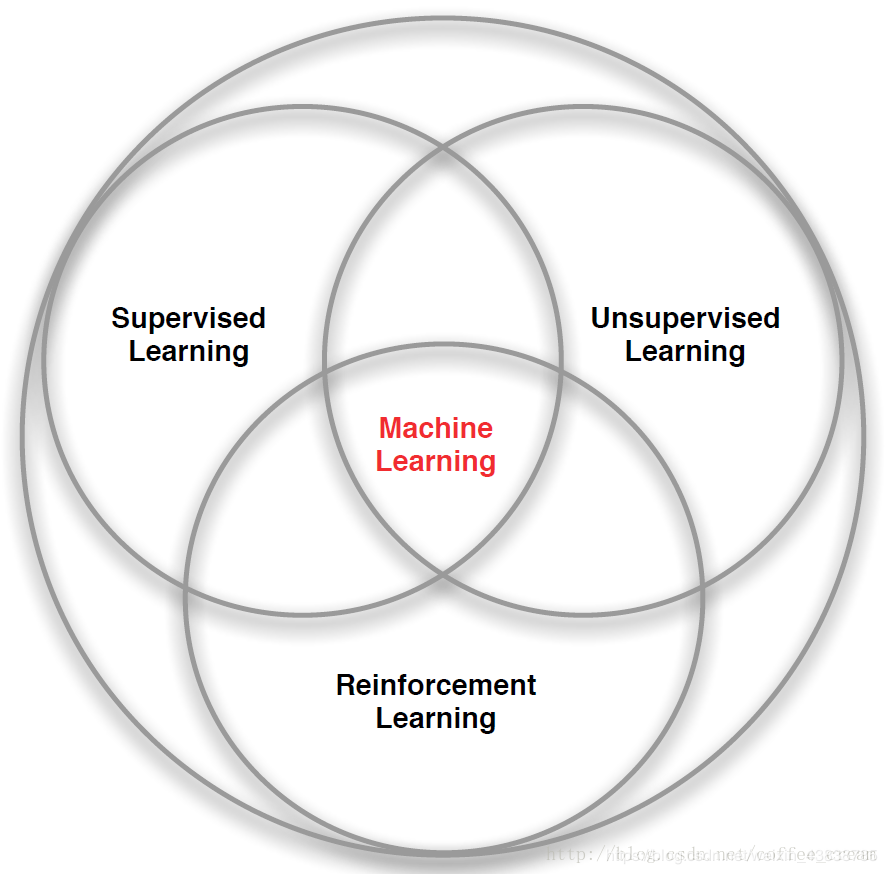
(1)有监督的学习是从一个已经标记的训练集中进行学习,训练集中每一个样本的特征可以视为是对该situation的描述,而其 label 可以视为是应该执行的正确的action,但是有监督的学习不能学习交互的情景,因为在交互的问题中获得期望行为的样例是非常不实际的,agent只能从自己的经历(experience)中进行学习,而experience中采取的行为并一定是最优的。这时利用RL就非常合适,因为RL不是利用正确的行为来指导,而是利用已有的训练信息来对行为进行评价。
(2)因为RL利用的并不是采取正确行动的experience,从这一点来看和无监督的学习确实有点像,但是还是不一样的,无监督的学习的目的可以说是从一堆未标记样本中发现隐藏的结构,而RL的目的是最大化 reward signal。
(3)总的来说,RL与其他机器学习算法不同的地方在于:其中没有监督者,只有一个reward信号;反馈是延迟的,不是立即生成的;时间在RL中具有重要的意义;agent的行为会影响之后一系列的data。
强化学习和之前学过的一些机器学习算法有着明显的不用,之前学的机器学习算法主要可以分为监督学习(分类)和非监督学习(聚类),而强化学习不同于监督学习和非监督学习,强化学习是通过奖励值来训练模型,而监督学习是通过训练数据和对应的标签来训练模型的,非监督学习没有标签也没有奖励值,是通过数据特征来训练模型的,而且强化学习的奖励值是在执行完动作后给出的,监督学习的标签是一开始就有的。
16.2 K-摇臂赌博机k-armed Bandit(也叫Multi-Armed Bandit)是赌场里的一种赌具。它有K个摇臂,投币后摇动摇臂,会有一定的概率吐出硬币。每个摇臂的吐币概率和数量有所不同。(有的机器只有1个摇臂,但可通过按钮设置不同的方案。)赌徒的目标是通过一定的策略获得最多的奖励(硬币)。
尽管在有的赌场中,每个摇臂的吐币概率和数量是已知的,但在本问题中,吐币概率和数量都是未知的。
由于每次摇臂都是独立事件,因此k-armed Bandit问题的另一个约束是:最大化单步奖励,即不考虑未来的奖励。
此外,k-armed Bandit亦不可能无限进行下去,其尝试总数是一定的(即投币数是一定的)。这也是该问题的一个隐含约束。
这里显然有两个最简单的策略:
exploration-only:将所有尝试机会平均分配给每个摇臂。这种策略可以很好的估计每个摇臂的奖励,然而却会失去很多选择最优摇臂的机会。
exploitation-only:只按下目前最优的摇臂。这种策略下有可能选不到最优的摇臂。
显然,欲奖励最大,需要在exploration和exploitation之间达成较好的折中。
ε-贪心算法贪心算法的基本思路:
ε是基于概率进行探索,ε作为随机选择一个摇臂的概率,那么1-ε的概率用于从平均奖赏最大的摇臂里面
选择。
算法实现的过程:
输入:摇臂的总数,K
k(小写) 表示当前选择第k个摇臂
奖赏函数 R
尝试次数 T
探索概率 ε
累计奖励用r表示累计奖励
Q(i) 表示第i个摇臂的平均奖赏
初始化 r=0,Q(i) = 0
For i in range(T):
If random()<ε:
k = Random.choice(range(1,K+1))
Esle:
k = argmax(Q(i))
v = R(k) (表示当前的奖赏)
r = r + v
Count(k) = count(k)+1
Print(“the reward is”.format®) # 输出累计奖赏
Python代码模拟仿真:
使用贪心算法实现
from numpy import random
K = [1,2,3,4,5] # 总共的摇臂数有5个
R = {1:2,2:3,3:5,4:1,5:9} # 各个摇臂对应的奖赏
prob = {1:0.6,2:0.5,3:0.2,4:0.7,5:0.05} #各个摇臂对应的概率吐币的概率
T = 10000
eplison = 0.1
count = dict(zip(list(range(1,6)),[0]*5)) # 计算每个摇臂的摇到的次数
r = 0
for i in range(T):
Q = dict(zip(list(range(1,6)),[0]*5))
if random.random() < eplison:
k = random.choice(K)
else:
k = max(Q,key=Q.get)
v = random.choice([R[k],0],p=[prob[k],1-prob[k]])
r += v
Q[k] = (Q[k]*count[k]+v)/(count[k]+1)
count[k] = count[k] + 1
print("end the reword is {}".format(r))
运行结果:
![]()
许多研究人员认为,基于模型的强化学习(MBRL)比无模型的强化学习(MFRL)具有更高的样本效率。但是,从根本上讲,这种说法是错误的。更细微的分析表明,使用神经网络时,MBRL方法可能比MFRL方法具有更高的采样效率,但仅适用于某些任务。此外,而基于模型的RL仅仅是开始。另一类算法,即基于同态的强化学习(HBRL),可能具有在诸如视觉干扰等具有高水平无关信息的任务上进一步提高样本效率的潜力。在这篇文章中,我们为这些想法提供了直观的证明。
16.4 免模型学习你是否认为我们用动态编程可以打造一个像Dota 2一样复杂的机器人呢?
很不幸,答案是否定的。因为Dota 2中的状态有很多,要收集所有具体状态几乎不可能。所以我们开始采用强化学习或者更具体的无模型学习。
16.5 值函数近似值函数近似——Large MDPs 的福音
对于具有大量状态空间和动作空间的MDPs,前面讲到的一些处理方法就不再适用了,可能会引起维度爆炸之类的问题。一个简单的方法就是用带有权重w参数的一个关于s的函数来表示近似的Vπ(s)或者qπ(s,a),以此建立值函数逼近器,这样我们就可以估算任何一个函数的值,并将其应用于状态数据库中,从而压缩了状态数据库的存储量。Value Function Approximation的思想大致就是如此。
模仿学习就是根据演示来学习,很多时候我们的任务没办法定义奖励,但是我们可以收集很多的数据给机器去学习,方法一般有两种,一种叫行为复制,一种叫逆向强化学习:

作者:理想007