Python深度强化学习之DQN算法原理详解
1 DQN算法简介
2 DQN算法原理
2.1 经验回放
2.2 目标网络
3 DQN算法伪代码
DQN算法是DeepMind团队提出的一种深度强化学习算法,在许多电动游戏中达到人类玩家甚至超越人类玩家的水准,本文就带领大家了解一下这个算法,论文的链接见下方。
论文:Human-level control through deep reinforcement learning | Nature
代码:后续会将代码上传到Github上...
1 DQN算法简介Q-learning算法采用一个Q-tabel来记录每个状态下的动作值,当状态空间或动作空间较大时,需要的存储空间也会较大。如果状态空间或动作空间连续,则该算法无法使用。因此,Q-learning算法只能用于解决离散低维状态空间和动作空间类问题。DQN算法的核心就是用一个人工神经网络 来代替Q-tabel,即动作价值函数。网络的输入为状态信息,输出为每个动作的价值,因此DQN算法可以用来解决连续状态空间和离散动作空间问题,无法解决连续动作空间类问题。针对连续动作空间类问题,后面blog会慢慢介绍。
来代替Q-tabel,即动作价值函数。网络的输入为状态信息,输出为每个动作的价值,因此DQN算法可以用来解决连续状态空间和离散动作空间问题,无法解决连续动作空间类问题。针对连续动作空间类问题,后面blog会慢慢介绍。
DQN算法是一种off-policy算法,当同时出现异策、自益和函数近似时,无法保证收敛性,容易出现训练不稳定或训练困难等问题。针对这些问题,研究人员主要从以下两个方面进行了改进。
(1)经验回放:将经验(当前状态st、动作at、即时奖励rt+1、下个状态st+1、回合状态done)存放在经验池中,并按照一定的规则采样。
(2)目标网络:修改网络的更新方式,例如不把刚学习到的网络权重马上用于后续的自益过程。
2.1 经验回放经验回放就是一种让经验概率分布变得稳定的技术,可以提高训练的稳定性。经验回放主要有“存储”和“回放”两大关键步骤:
存储:将经验以(st,at,rt+1,st+1,done)形式存储在经验池中。
回放:按照某种规则从经验池中采样一条或多条经验数据。
从存储的角度来看,经验回放可以分为集中式回放和分布式回放:
集中式回放:智能体在一个环境中运行,把经验统一存储在经验池中。
分布式回放:多个智能体同时在多个环境中运行,并将经验统一存储在经验池中。由于多个智能体同时生成经验,所以能够使用更多资源的同时更快地收集经验。
从采样的角度来看,经验回放可以分为均匀回放和优先回放:
均匀回放:等概率从经验池中采样经验。
优先回放:为经验池中每条经验指定一个优先级,在采样经验时更倾向于选择优先级更高的经验。一般的做法是,如果某条经验(例如经验)的优先级为,那么选取该经验的概率为:

优先回放可以具体参照这篇论文:优先经验回放
经验回放的优点:
1.在训练Q网络时,可以打破数据之间的相关性,使得数据满足独立同分布,从而减小参数更新的方差,提高收敛速度。
2.能够重复使用经验,数据利用率高,对于数据获取困难的情况尤其有用。
经验回放的缺点:
无法应用于回合更新和多步学习算法。但是将经验回放应用于Q学习,就规避了这个缺点。
代码中采用集中式均匀回放,具体如下:
import numpy as np
class ReplayBuffer:
def __init__(self, state_dim, action_dim, max_size, batch_size):
self.mem_size = max_size
self.batch_size = batch_size
self.mem_cnt = 0
self.state_memory = np.zeros((self.mem_size, state_dim))
self.action_memory = np.zeros((self.mem_size, ))
self.reward_memory = np.zeros((self.mem_size, ))
self.next_state_memory = np.zeros((self.mem_size, state_dim))
self.terminal_memory = np.zeros((self.mem_size, ), dtype=np.bool)
def store_transition(self, state, action, reward, state_, done):
mem_idx = self.mem_cnt % self.mem_size
self.state_memory[mem_idx] = state
self.action_memory[mem_idx] = action
self.reward_memory[mem_idx] = reward
self.next_state_memory[mem_idx] = state_
self.terminal_memory[mem_idx] = done
self.mem_cnt += 1
def sample_buffer(self):
mem_len = min(self.mem_size, self.mem_cnt)
batch = np.random.choice(mem_len, self.batch_size, replace=True)
states = self.state_memory[batch]
actions = self.action_memory[batch]
rewards = self.reward_memory[batch]
states_ = self.next_state_memory[batch]
terminals = self.terminal_memory[batch]
return states, actions, rewards, states_, terminals
def ready(self):
return self.mem_cnt > self.batch_size
2.2 目标网络
对于基于自益的Q学习,动作价值估计和权重有关。当权重变化时,动作价值的估计也会发生变化。在学习的过程中,动作价值试图追逐一个变化的回报,容易出现不稳定的情况。
目标网络是在原有的神经网络之外重新搭建一个结构完全相同的网络。原先的网络称为评估网络,新构建的网络称为目标网络。在学习过程中,使用目标网络进行自益得到回报的评估值,作为学习目标。在更新过程中,只更新评估网络的权重,而不更新目标网络的权重。这样,更新权重时针对的目标不会在每次迭代都发生变化,是一个固定的目标。在更新一定次数后,再将评估网络的权重复制给目标网络,进而进行下一批更新,这样目标网络也能得到更新。由于在目标网络没有变化的一段时间内回报的估计是相对固定的,因此目标网络的引入增加了学习的稳定性。
目标网络的更新方式:
上述在一段时间内固定目标网络,一定次数后将评估网络权重复制给目标网络的更新方式为硬更新(hard update),即

其中表示目标网络权重,表示评估网络权重。
另外一种常用的更新方式为软更新(soft update),即引入一个学习率,将旧的目标网络参数和新的评估网络参数直接做加权平均后的值赋值给目标网络
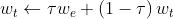
学习率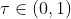

DQN算法的实现代码为:
import torch as T
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
from buffer import ReplayBuffer
device = T.device("cuda:0" if T.cuda.is_available() else "cpu")
class DeepQNetwork(nn.Module):
def __init__(self, alpha, state_dim, action_dim, fc1_dim, fc2_dim):
super(DeepQNetwork, self).__init__()
self.fc1 = nn.Linear(state_dim, fc1_dim)
self.fc2 = nn.Linear(fc1_dim, fc2_dim)
self.q = nn.Linear(fc2_dim, action_dim)
self.optimizer = optim.Adam(self.parameters(), lr=alpha)
self.to(device)
def forward(self, state):
x = T.relu(self.fc1(state))
x = T.relu(self.fc2(x))
q = self.q(x)
return q
def save_checkpoint(self, checkpoint_file):
T.save(self.state_dict(), checkpoint_file, _use_new_zipfile_serialization=False)
def load_checkpoint(self, checkpoint_file):
self.load_state_dict(T.load(checkpoint_file))
class DQN:
def __init__(self, alpha, state_dim, action_dim, fc1_dim, fc2_dim, ckpt_dir,
gamma=0.99, tau=0.005, epsilon=1.0, eps_end=0.01, eps_dec=5e-4,
max_size=1000000, batch_size=256):
self.tau = tau
self.gamma = gamma
self.epsilon = epsilon
self.eps_min = eps_end
self.eps_dec = eps_dec
self.batch_size = batch_size
self.action_space = [i for i in range(action_dim)]
self.checkpoint_dir = ckpt_dir
self.q_eval = DeepQNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
fc1_dim=fc1_dim, fc2_dim=fc2_dim)
self.q_target = DeepQNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
fc1_dim=fc1_dim, fc2_dim=fc2_dim)
self.memory = ReplayBuffer(state_dim=state_dim, action_dim=action_dim,
max_size=max_size, batch_size=batch_size)
self.update_network_parameters(tau=1.0)
def update_network_parameters(self, tau=None):
if tau is None:
tau = self.tau
for q_target_params, q_eval_params in zip(self.q_target.parameters(), self.q_eval.parameters()):
q_target_params.data.copy_(tau * q_eval_params + (1 - tau) * q_target_params)
def remember(self, state, action, reward, state_, done):
self.memory.store_transition(state, action, reward, state_, done)
def choose_action(self, observation, isTrain=True):
state = T.tensor([observation], dtype=T.float).to(device)
actions = self.q_eval.forward(state)
action = T.argmax(actions).item()
if (np.random.random() < self.epsilon) and isTrain:
action = np.random.choice(self.action_space)
return action
def learn(self):
if not self.memory.ready():
return
states, actions, rewards, next_states, terminals = self.memory.sample_buffer()
batch_idx = np.arange(self.batch_size)
states_tensor = T.tensor(states, dtype=T.float).to(device)
rewards_tensor = T.tensor(rewards, dtype=T.float).to(device)
next_states_tensor = T.tensor(next_states, dtype=T.float).to(device)
terminals_tensor = T.tensor(terminals).to(device)
with T.no_grad():
q_ = self.q_target.forward(next_states_tensor)
q_[terminals_tensor] = 0.0
target = rewards_tensor + self.gamma * T.max(q_, dim=-1)[0]
q = self.q_eval.forward(states_tensor)[batch_idx, actions]
loss = F.mse_loss(q, target.detach())
self.q_eval.optimizer.zero_grad()
loss.backward()
self.q_eval.optimizer.step()
self.update_network_parameters()
self.epsilon = self.epsilon - self.eps_dec if self.epsilon > self.eps_min else self.eps_min
def save_models(self, episode):
self.q_eval.save_checkpoint(self.checkpoint_dir + 'Q_eval/DQN_q_eval_{}.pth'.format(episode))
print('Saving Q_eval network successfully!')
self.q_target.save_checkpoint(self.checkpoint_dir + 'Q_target/DQN_Q_target_{}.pth'.format(episode))
print('Saving Q_target network successfully!')
def load_models(self, episode):
self.q_eval.load_checkpoint(self.checkpoint_dir + 'Q_eval/DQN_q_eval_{}.pth'.format(episode))
print('Loading Q_eval network successfully!')
self.q_target.load_checkpoint(self.checkpoint_dir + 'Q_target/DQN_Q_target_{}.pth'.format(episode))
print('Loading Q_target network successfully!')
算法仿真环境是在gym库中的LunarLander-v2环境,因此需要先配置好gym库。进入Aanconda中对应的Python环境中,执行下面的指令
pip install gym
但是,这样安装的gym库只包括少量的内置环境,如算法环境、简单文字游戏环境和经典控制环境,无法使用LunarLander-v2。
训练脚本如下:
import gym
import numpy as np
import argparse
from DQN import DQN
from utils import plot_learning_curve, create_directory
parser = argparse.ArgumentParser()
parser.add_argument('--max_episodes', type=int, default=500)
parser.add_argument('--ckpt_dir', type=str, default='./checkpoints/DQN/')
parser.add_argument('--reward_path', type=str, default='./output_images/avg_reward.png')
parser.add_argument('--epsilon_path', type=str, default='./output_images/epsilon.png')
args = parser.parse_args()
def main():
env = gym.make('LunarLander-v2')
agent = DQN(alpha=0.0003, state_dim=env.observation_space.shape[0], action_dim=env.action_space.n,
fc1_dim=256, fc2_dim=256, ckpt_dir=args.ckpt_dir, gamma=0.99, tau=0.005, epsilon=1.0,
eps_end=0.05, eps_dec=5e-4, max_size=1000000, batch_size=256)
create_directory(args.ckpt_dir, sub_dirs=['Q_eval', 'Q_target'])
total_rewards, avg_rewards, eps_history = [], [], []
for episode in range(args.max_episodes):
total_reward = 0
done = False
observation = env.reset()
while not done:
action = agent.choose_action(observation, isTrain=True)
observation_, reward, done, info = env.step(action)
agent.remember(observation, action, reward, observation_, done)
agent.learn()
total_reward += reward
observation = observation_
total_rewards.append(total_reward)
avg_reward = np.mean(total_rewards[-100:])
avg_rewards.append(avg_reward)
eps_history.append(agent.epsilon)
print('EP:{} reward:{} avg_reward:{} epsilon:{}'.
format(episode + 1, total_reward, avg_reward, agent.epsilon))
if (episode + 1) % 50 == 0:
agent.save_models(episode + 1)
episodes = [i for i in range(args.max_episodes)]
plot_learning_curve(episodes, avg_rewards, 'Reward', 'reward', args.reward_path)
plot_learning_curve(episodes, eps_history, 'Epsilon', 'epsilon', args.epsilon_path)
if __name__ == '__main__':
main()
训练时还会用到画图函数和创建文件夹函数,我将他们另外放在一个utils.py脚本中,具体代码如下:
import os
import matplotlib.pyplot as plt
def plot_learning_curve(episodes, records, title, ylabel, figure_file):
plt.figure()
plt.plot(episodes, records, linestyle='-', color='r')
plt.title(title)
plt.xlabel('episode')
plt.ylabel(ylabel)
plt.show()
plt.savefig(figure_file)
def create_directory(path: str, sub_dirs: list):
for sub_dir in sub_dirs:
if os.path.exists(path + sub_dir):
print(path + sub_dir + ' is already exist!')
else:
os.makedirs(path + sub_dir, exist_ok=True)
print(path + sub_dir + ' create successfully!')
仿真结果如下图所示:

通过平均奖励曲线可以看出,大概迭代到400步左右时算法趋于收敛。
到此这篇关于Python深度强化学习之DQN算法原理详解的文章就介绍到这了,更多相关Python DQN算法内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!