【PyTorch学习笔记1】MNIST手写数字识别之MLP实现
在本笔记中,我们将以多层感知机(multilayer perceptron,MLP)为例,介绍多层神经网络的相关概念,并将其运用到最基础的MNIST数据集分类任务中,同时展示相关代码。本笔记主要从下面四个方面展开:
文章目录1 多层感知机(MLP)理论知识1.1 隐藏层1.2 激活函数1.3 多层感知机1.4 交叉熵(cross entropy)损失函数2. MNIST数据集简介3. 代码详解及结果展示4. 心得体会 1 多层感知机(MLP)理论知识 1.1 隐藏层多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。隐藏层位于输入层和输出层之间。下图展示了一个多层感知机的神经网络图,它含有一个隐藏层,该层中有5个隐藏单元。
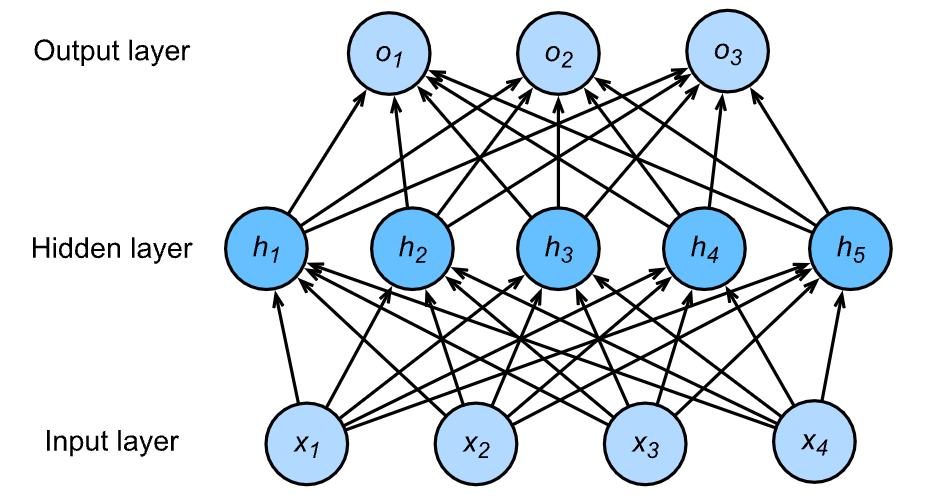
在上图所示的多层感知机中,输入和输出个数分别为4和3,中间的隐藏层中包含了5个隐藏单元(hidden unit)。由于输入层不涉及计算,上图中的多层感知机的层数为2。由上图可见,隐藏层中的神经元和输入层中各个输入完全连接,输出层中的神经元和隐藏层中的各个神经元也完全连接。因此,多层感知机中的隐藏层和输出层都是全连接层。
具体来说,给定一个小批量样本X∈Rn×d\boldsymbol{X} \in \mathbb{R}^{n \times d}X∈Rn×d,其批量大小为nnn,输入个数为ddd。假设多层感知机只有一个隐藏层,其中隐藏单元个数为hhh。记隐藏层的输出(也称为隐藏层变量或隐藏变量)为H\boldsymbol{H}H,有H∈Rn×h\boldsymbol{H} \in \mathbb{R}^{n \times h}H∈Rn×h。因为隐藏层和输出层均是全连接层,可以设隐藏层的权重参数和偏差参数分别为Wh∈Rd×h\boldsymbol{W}_h \in \mathbb{R}^{d \times h}Wh∈Rd×h和 bh∈R1×h\boldsymbol{b}_h \in \mathbb{R}^{1 \times h}bh∈R1×h,输出层的权重和偏差参数分别为Wo∈Rh×q\boldsymbol{W}_o \in \mathbb{R}^{h \times q}Wo∈Rh×q和bo∈R1×q\boldsymbol{b}_o \in \mathbb{R}^{1 \times q}bo∈R1×q。
我们先来看一种含单隐藏层的多层感知机的设计。其输出O∈Rn×q\boldsymbol{O} \in \mathbb{R}^{n \times q}O∈Rn×q的计算为H=XWh+bhO=HWo+bo \begin{aligned}\boldsymbol{H} &=\boldsymbol{X}\boldsymbol{W}_h + \boldsymbol{b}_h\\ \boldsymbol{O} &= \boldsymbol{H} \boldsymbol{W}_o +\boldsymbol{b}_o\end{aligned} HO=XWh+bh=HWo+bo也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来,可以得到O=(XWh+bh)Wo+bo=XWhWo+bhWo+bo. \boldsymbol{O} = (\boldsymbol{X} \boldsymbol{W}_h + \boldsymbol{b}_h)\boldsymbol{W}_o + \boldsymbol{b}_o = \boldsymbol{X} \boldsymbol{W}_h\boldsymbol{W}_o + \boldsymbol{b}_h \boldsymbol{W}_o + \boldsymbol{b}_o. O=(XWh+bh)Wo+bo=XWhWo+bhWo+bo.从联立后的式子可以看出,虽然神经网络引入了隐藏层,却依然等价于一个单层神经网络:其中输出层权重参数为WhWo\boldsymbol{W}_h\boldsymbol{W}_oWhWo,偏差参数为bhWo+bo\boldsymbol{b}_h \boldsymbol{W}_o + \boldsymbol{b}_obhWo+bo。不难发现,即便再添加更多的隐藏层,以上设计依然只能与仅含输出层的单层神经网络等价。
1.2 激活函数上述问题的根源在于全连接层只是对数据做仿射变换(affine transformation),而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换,例如对隐藏变量使用按元素运算的非线性函数进行变换,然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数(activation function)。
由于后续的MNIST分类任务属于图像识别分类任务,而如今在图像识别领域中用的最多的激活函数是ReLU函数以及由它衍生出来的一批函数,所以接下来着重介绍ReLU函数。
ReLU(rectified linear unit)函数提供了一个很简单的非线性变换。给定元素xxx,该函数定义为ReLU(x)=max(x,0).\text{ReLU}(x) = \max(x, 0).ReLU(x)=max(x,0).可以看出,ReLU函数只保留正数元素,并将负数元素清零。为了直观地观察这一非线性变换,我们先定义一个绘图函数xyplot。
import numpy
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.autograd import Variable #求梯度必备函数
def xyplot(x_vals,y_vals,name):
x_vals=x_vals.numpy()
y_vals=y_vals.numpy()
plt.plot(x_vals,y_vals)
plt.xlabel('x')
plt.ylabel(name+'(x)')
我们接下来通过torch提供的relu函数来绘制ReLU函数。可以看到,该激活函数是一个两段线性函数。
x=Variable(torch.arange(-8.0,8.0,0.1),requires_grad=True) #对Tensor变量进行封装,使得可以计算其梯度
y=torch.nn.functional.relu(x) #与nn.relu区分开
xyplot(x,y,'relu')
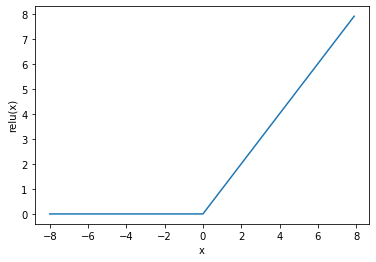
显然,当输入为负数时,ReLU函数的导数为0;当输入为正数时,ReLU函数的导数为1。尽管输入为0时ReLU函数不可导,但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。
y.backward(torch.ones_like(x),retain_graph=True)
xyplot(x,x.grad,"grad of relu")

优点:
简单高效:不涉及指数等运算; 一定程度缓解梯度消失问题:因为导数为 1,不会像 sigmoid 那样由于导数较小,而导致连乘得到的梯度逐渐消失。缺点:
dying Relu即网络的部分分量都永远不会更新,可以参考:What is the "dying ReLU" problem in neural networks? 1.3 多层感知机多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号,多层感知机按以下方式计算输出:H=ϕ(XWh+bh)O=HWo+bo \begin{aligned}\boldsymbol{H} &= \phi(\boldsymbol{X} \boldsymbol{W}_h + \boldsymbol{b}_h)\\ \boldsymbol{O} &= \boldsymbol{H} \boldsymbol{W}_o + \boldsymbol{b}_o \end{aligned} HO=ϕ(XWh+bh)=HWo+bo其中ϕ\phiϕ表示激活函数。在分类问题中,我们可以对输出O\boldsymbol{O}O做softmax运算,并使用softmax回归中的交叉熵损失函数。在回归问题中,我们将输出层的输出个数设为1,并将输出O\boldsymbol{O}O直接提供给线性回归中使用的平方损失函数。
1.4 交叉熵(cross entropy)损失函数我们已经知道,softmax运算将输出变换成一个合法的类别预测分布。实际上,真实标签也可以用类别分布表达:对于样本iii,我们构造向量y(i)∈Rq\boldsymbol{y}^{(i)}\in \mathbb{R}^{q}y(i)∈Rq ,使其第y(i)y^{(i)}y(i)(样本iii类别的离散数值)个元素为1,其余为0。这样我们的训练目标可以设为使预测概率分布y^(i)\boldsymbol{\hat y}^{(i)}y^(i)尽可能接近真实的标签概率分布y(i)\boldsymbol{y}^{(i)}y(i)。
我们可以像线性回归那样使用平方损失函数∣∣y^(i)−y(i)∣∣2/2||\boldsymbol{\hat y}^{(i)}-\boldsymbol{y}^{(i)}||^2/2∣∣y^(i)−y(i)∣∣2/2。然而,想要预测分类结果正确,我们其实并不需要预测概率完全等于标签概率。例如,在图像分类的例子里,如果y(i)=3y^{(i)}=3y(i)=3,那么我们只需要y^3(i)\hat{y}^{(i)}_3y^3(i)比其他两个预测值y^1(i)\hat{y}^{(i)}_1y^1(i)和y^2(i)\hat{y}^{(i)}_2y^2(i)大就行了。即使y^3(i)\hat{y}^{(i)}_3y^3(i)值为0.6,不管其他两个预测值为多少,类别预测均正确。而平方损失则过于严格,例如y^1(i)=y^2(i)=0.2\hat y^{(i)}_1=\hat y^{(i)}_2=0.2y^1(i)=y^2(i)=0.2比y^1(i)=0,y^2(i)=0.4\hat y^{(i)}_1=0, \hat y^{(i)}_2=0.4y^1(i)=0,y^2(i)=0.4的损失要小很多,虽然两者都有同样正确的分类预测结果。
改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中,交叉熵(cross entropy)是一个常用的衡量方法:H(y(i),y^(i))=−∑j=1qyj(i)logy^j(i),H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ) = -\sum_{j=1}^q y_j^{(i)} \log \hat y_j^{(i)},H(y(i),y^(i))=−j=1∑qyj(i)logy^j(i),其中带下标的yj(i)y_j^{(i)}yj(i)是向量y(i)\boldsymbol y^{(i)}y(i)中非0即1的元素,需要注意将它与样本iii类别的离散数值,即不带下标的y(i)y^{(i)}y(i)区分。在上式中,我们知道向量y(i)\boldsymbol y^{(i)}y(i)中只有第y(i)y^{(i)}y(i)个元素y(i)y(i)y^{(i)}{y^{(i)}}y(i)y(i)为1,其余全为0,于是H(y(i),y^(i))=−logy^y(i)(i)H(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}) = -\log \hat y{y^{(i)}}^{(i)}H(y(i),y^(i))=−logy^y(i)(i)。也就是说,交叉熵只关心对正确类别的预测概率,因为只要其值足够大,就可以确保分类结果正确。当然,遇到一个样本有多个标签时,例如图像里含有不止一个物体时,我们并不能做这一步简化。但即便对于这种情况,交叉熵同样只关心对图像中出现的物体类别的预测概率。
假设训练数据集的样本数为nnn,交叉熵损失函数定义为
ℓ(Θ)=1n∑i=1nH(y(i),y^(i)),\ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ),ℓ(Θ)=n1i=1∑nH(y(i),y^(i)),其中Θ\boldsymbol{\Theta}Θ代表模型参数。同样地,如果每个样本只有一个标签,那么交叉熵损失可以简写成ℓ(Θ)=−(1/n)∑i=1nlogy^y(i)(i)\ell(\boldsymbol{\Theta}) = -(1/n) \sum_{i=1}^n \log \hat y_{y^{(i)}}^{(i)}ℓ(Θ)=−(1/n)∑i=1nlogy^y(i)(i)。从另一个角度来看,我们知道最小化ℓ(Θ)\ell(\boldsymbol{\Theta})ℓ(Θ)等价于最大化exp(−nℓ(Θ))=∏i=1ny^y(i)(i)\exp(-n\ell(\boldsymbol{\Theta}))=\prod_{i=1}^n \hat y_{y^{(i)}}^{(i)}exp(−nℓ(Θ))=∏i=1ny^y(i)(i),即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
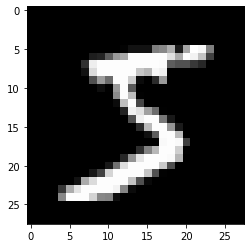
黑底白字,黑底用0表示,白字用0~1之间的浮点数表示,越接近1,颜色越亮。 3. 代码详解及结果展示
import torch
import torch.nn as nn
import torchvision #torch中用来处理图像的库
from torchvision import datasets,transforms
import matplotlib.pyplot as plt
torchvision是PyTorch中专门用来处理图像的库,这个包中有四个大类:
torchvision.datasets用来进行数据加载,PyTorch团队在这个包中帮我们提前处理好了很多很多图片数据集,例如MNISTCOCO、Imagenet-12、CIFAR等。
torchvision.models为我们提供了已经训练好的模型,让我们可以加载之后,直接使用。
torchvision.transforms为我们提供了一般的图像转换操作类,具体操作可参照后文。
torchvision.utils可用于将图片排列成网格形状或者把指定的Tensor保存成图片格式。
#设置一些超参
num_epochs = 1 #训练的周期
batch_size = 100 #批训练的数量
learning_rate = 0.001 #学习率(0.1,0.01,0.001)
一般在神经网络的训练中我们需要导入上述的三个超参数(超参数指的是神经网络外部可由设计者调节的参数,要与神经网络内部的权重和偏置区分开,超参选取的好坏直接影响到模型的泛化能力,故近些年来也有很多人在研究关于超参调节的一些工作)
num_epochs神经网络训练的周期,对于大型神经网络训练一次肯定是不够的,但是次数太多又会影响效率。
batch_size批训练的数量,如果一次训练一张图片,60000张图片将多浪费时间,而且更新参数也太频繁,所以我们可以选择一批一批的训练,对于输入数据可以看成是增加了矩阵的行数,输出数据也是增加了矩阵的行数,这样可以大大的提高训练的效率。这个参数的意义理解起来可能一开始会有点困难,但是随着读者后续对于神经网络输入数据维度的理解越来越深之后,这个概念便不难理解。
learning_rate学习率,主要用于后面优化器的参数调节。
#导入训练数据
train_dataset = datasets.MNIST(root='E:/MNIST/', #数据集保存路径
train=True, #是否作为训练集
transform=transforms.ToTensor(), #数据如何处理, 可以自己自定义
download=False) #路径下没有的话, 可以下载
#导入测试数据
test_dataset = datasets.MNIST(root='E:/MNIST/',
train=False,
transform=transforms.ToTensor())
由于MNIST是比较经典的数据集,Torch里面已经内嵌了很多方便的框架来处理它,在导入数据的这一步就可以看得出来。
datasets.MNIST中的第一个key和第四个key相对应,download=True说明我们需要从网上下载这个数据集到root路径并保存,第一次下载好后就设置download=False不用再第二次下载。
train=True即说明此时导入的数据为训练数据,相应的train=False即说明此时导入的数据为测试数据。
transform=transforms.ToTensor()也是非常关键的一步,就是把数据集中的图片格式变为Tensor格式方便后面的处理。
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, #分批
batch_size=batch_size,
shuffle=True) #随机分批
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
这一步即为数据的批处理操作,目的已经在第一个代码块说明。torch.utils.data.DataLoader提供了数据批处理的函数。
dataset=train_dataset表示要进行批处理的数据是什么。
batch_size=batch_size第二个key表示每一批的数量是多少,分到最后没有这么多了也会自动归为一批,在这里之前设置的数量为100.
shuffle=True这个key也是一个理解的难点,即选取每一批中的数据时我要随机的从数据集中选取,这样的话就会避免因为数据集自身的规律性而导致的模型泛化能力降低的问题。当然只需要在训练集中采取这一步就可以了,测试集中有没有无所谓。
class MLP(nn.Module): #继承nn.module
def __init__(self):
super(MLP, self).__init__() #继承的作用
self.layer1 = nn.Linear(784,300)
self.relu = nn.ReLU()
self.layer2 = nn.Linear(300,10)
def forward(self,x): #网络传播的结构
x = x.reshape(-1, 28*28)
x = self.layer1(x)
x = self.relu(x)
y = self.layer2(x)
return y
这一模块就相当于在搭建神经网络了,笔者形象的把这一过程称之为指导一个人爬楼。def __init__(self)这一个函数相当于首先建一个楼,def forward(self,x)这一个函数相当于告诉我这个人应该按照一个什么顺序上楼,例如我是按顺序上楼还是跳级上楼。
self.layer1 = nn.Linear(784,300)即第一层是一个全连接线性层,我的输入数据维度为784,即28*28;输出数据维度为300(这个属于中间变量可人为设定,只要和下一层的输入匹配就可以了)。
self.relu = nn.ReLU()即第二层为非线性层,利用ReLU函数将数据非线性化处理,处理的原因在第一部分理论知识中已经阐述,此处需要注意非线性化处理不改变数据的维度。
self.layer2 = nn.Linear(300,10)即第三层依然是一个全连接线性层,此时的第一个维度即为第一个线性层输出的维度,第二个维度即为最后我们需要的输出分类,即0~9的一个可能性大小。
x = x.reshape(-1, 28*28)对于神经网络每一次的输入都需要是一个行向量,所以要把一张28*28的图片拉直为一条向量,但是我们进行了批处理,所以我们是100张图片一起放入,所以我们需要把100*1*28*28的一个四维数据变成100*784的一个二维矩阵,-1代表的是reshape可根据输入数据的大小和指定的其中一个维度自动计算出另一个维度。因为我们不可能每一步都手动的计算出数据维度的大小,这一个技巧特别在大型网络中比较受用。
mlp = MLP() #类的实例化
上一步定义了一个我自己设定的类,现在我要将它实例化,并且在这个实例化的过程中,这个神经网络中的参数已经通过一定的规则赋予了初值(是不是很智能!)
loss_func = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(mlp.parameters(), lr=learning_rate)
在正式训练之前,我们需要引入两个很重要的功能。
nn.CrossEntropyLoss()此处定义了此次训练的损失函数交叉熵函数,当然这个函数里面包括了softmax处理以及交叉熵的计算。
torch.optim.Adam(mlp.parameters(), lr=learning_rate)此处定义了最小化交叉熵函数的优化器,使用了Adam优化方法(当然传统的SGD也可以,只是Adam中添加了动量项,相比普通的SGD收敛更快。但是,凡事都有一个但是,什么都不会那么绝对,在某些其他具体问题中展示出了SGD的优势,至于具体的原因,笔者下来也会研究)。后面的第一个key为需要更新的参数,第二个key为学习率,当然此处应该还有动量项key,这里没有指定即代表使用默认值。
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
outputs = mlp(images)
loss = loss_func(outputs, labels)
optimizer.zero_grad() #清零梯度
loss.backward() #反向求梯度
optimizer.step()
if (i+1) % 100 == 0:
print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch + 1, num_epochs, loss.item()))
此模块是训练神经网络,对于每一个训练周期每一批训练数据有如下步骤:
outputs = mlp(images)传入分批图片数据,输出一个矩阵,这个矩阵的每一行都代表着某张照片的分类向量。
loss = loss_func(outputs, labels)计算输出和正确标签的交叉熵。
optimizer.zero_grad()用于清零梯度,释放内存。(至于为什么要这样,我还没有得到一个很好地解释)
loss.backward()对于之前求的损失函数反向求梯度。
optimizer.step()利用我们选定的优化方法,此处为Adam,更新神经网络中的参数。
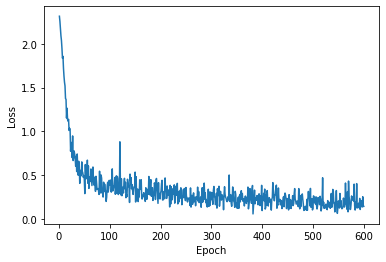
最后再用格式化输出工具或者作图记录下我们计算的loss的变化。
#测试模型
mlp.eval() #测试模式,关闭正则化
correct = 0
total = 0
for images, labels in test_loader:
outputs = mlp(images)
_, predicted = torch.max(outputs, 1) #返回值和索引
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('测试准确率: {:.4f}'.format(100.0*correct/total))
最后这一模块便是检验我们的神经网络训练的如何。
mlp.eval()将神经网络的模式切换成测试模式,即关闭dropout功能。(dropout功能是在训练网络的过程中随机将某两层之间的矩阵按指定的概率置零,增强模型的泛化性能,至于为什么能增强,笔者也在寻找中)
通过运算最后的准确率达到95%左右。
4. 心得体会 MNIST数据集分类任务在整个Deep Learning的领域中可以算是比较基础的一个小部分,有很多方法都可以很好地解决它,比较适合初学者入手,当然也算我一个。 但是在梳理的过程中,里面所牵扯出的一些小点其实与实现分类任务本身相比还是很难理解的,并且还有一些甚至到目前都没有一个很好的解释,不过也正是这样才促进了可解释性深度学习的发展。 在完成这篇博客的过程中还是学到了很多。比如使用markdown语言来分享一些自己的所学所想;比如通过思考怎么给大家讲清楚查了很多额外的资料;再比如自己组织语言的能力…当然也很感谢老师以及师兄的帮助。作者:XiaYuFeng15