Pytorch中Softmax与LogSigmoid的对比分析

Phaedra ·

更新时间:2024-11-13

· 1965 次阅读

Pytorch中Softmax与LogSigmoid的对比 torch.nn.Softmax

作用：

1、将Softmax函数应用于输入的n维Tensor，重新改变它们的规格，使n维输出张量的元素位于[0,1]范围内，并求和为1。

2、返回的Tensor与原Tensor大小相同，值在[0，1]之间。

3、不建议将其与NLLLoss一起使用，可以使用LogSoftmax代替之。

4、Softmax的公式：

参数：

维度，待使用softmax计算的维度。

例子：


# 随机初始化一个tensor
a = torch.randn(2, 3)
print(a) # 输出tensor
# 初始化一个Softmax计算对象，在输入tensor的第2个维度上进行此操作
m = nn.Softmax(dim=1)
# 将a进行softmax操作
output = m(a)
print(output) # 输出tensor
tensor([[ 0.5283,  0.3922, -0.0484],
        [-1.6257, -0.4775,  0.5645]])
tensor([[0.4108, 0.3585, 0.2307],
        [0.0764, 0.2408, 0.6828]])

可以看见的是，无论输入的tensor中的值为正或为负，输出的tensor中的值均为正值，且加和为1。

当m的参数dim=1时，输出的tensor将原tensor按照行进行softmax操作；当m的参数为dim=0时，输出的tensor将原tensor按照列进行softmax操作。

深度学习拓展：

一般来说，Softmax函数会用于分类问题上。例如，在VGG等深度神经网络中，图像经过一系列卷积、池化操作后，我们可以得到它的特征向量，为了进一步判断此图像中的物体属于哪个类别，我们会将该特征向量变为：类别数 * 各类别得分的形式，为了将得分转换为概率值，我们会将该向量再经过一层Softmax处理。

torch.nn.LogSigmoid

公式：

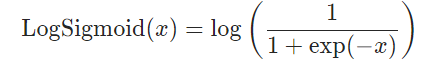
函数图：

可以见得，函数值在[0, -]之间，输入值越大函数值距离0越近，在一定程度上解决了梯度消失问题。

例子：


a = [[ 0.5283,  0.3922, -0.0484],
    [-1.6257, -0.4775,  0.5645]]
a = torch.tensor(a)
lg = nn.LogSigmoid()
lgoutput = lg(a)
print(lgoutput)
tensor([[-0.4635, -0.5162, -0.7176],
        [-1.8053, -0.9601, -0.4502]])

二者比较：


import torch
import torch.nn as nn
# 设置a为 2*3  的tensor
a = [[ 0.5283,  0.3922, -0.0484],
    [-1.6257, -0.4775,  0.5645]]
a = torch.tensor(a)
print(a)
print('a.mean:', a.mean(1, True)) # 输出a的 行平均值
m = nn.Softmax(dim=1) # 定义Softmax函数，dim=1表示为按行计算
lg = nn.LogSigmoid() # 定义LogSigmoid函数
output = m(a)
print(output)
# 输出a经过Softmax的结果的行平均值
print('output.mean:', output.mean(1, True)) 
lg_output = lg(a)
print(lg_output)
# 输出a经过LogSigmoid的结果的行平均值
print('lgouput.mean:', lg_output.mean(1, True)) 
# 结果：
tensor([[ 0.5283,  0.3922, -0.0484],
        [-1.6257, -0.4775,  0.5645]])
a.mean: tensor(-0.1111)
tensor([[0.4108, 0.3585, 0.2307],
        [0.0764, 0.2408, 0.6828]])
output.mean: tensor([[0.3333], [0.3333]]) # 经过Softmax的结果的行平均值
tensor([[-0.4635, -0.5162, -0.7176],
        [-1.8053, -0.9601, -0.4502]])
lgouput.mean: tensor([[-0.5658], [-1.0719]]) # 经过LogSigmoid的结果的行平均值

由上可知，继续考虑分类问题，相同的数据，经过Softmax和LogSigmoid处理后，若取最大概率值对应类别作为分类结果，那么：

1、第一行数据经过Softmax后，会选择第一个类别；经过LogSigmoid后，会选择第一个。

2、第二行数据经过Softmax后，会选择第三个类别；经过LogSigmoid后，会选择第三个。

3、一般来说，二者在一定程度上区别不是很大，由于sigmoid函数存在梯度消失问题，所以被使用的场景不多。

4、但是在多分类问题上，可以尝试选择Sigmoid函数来作为分类函数，因为Softmax在处理多分类问题上，会更容易出现各项得分十分相近的情况。瓶颈值可以根据实际情况定。

nn.Softmax()与nn.LogSoftmax()

nn.Softmax()计算出来的值，其和为1，也就是输出的是概率分布，具体公式如下：

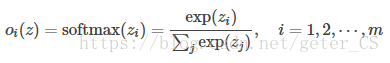
这保证输出值都大于0，在0,1范围内。

而nn.LogSoftmax()公式如下：

由于softmax输出都是0-1之间的，因此logsofmax输出的是小于0的数，

softmax求导：

logsofmax求导：

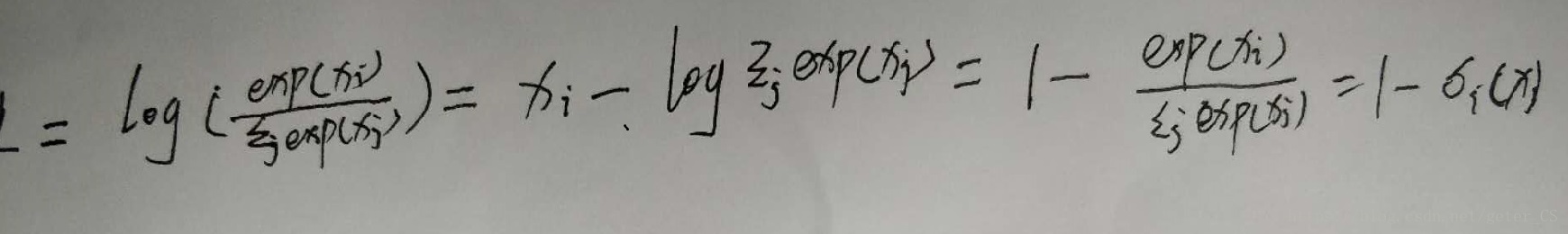
例子：


import torch.nn as nn
import torch
import numpy as np


layer1=nn.Softmax()
layer2=nn.LogSoftmax()
input=np.asarray([2,3])
input=Variable(torch.Tensor(input))
output1=layer1(input)
output2=layer2(input)
print('output1:',output1)
print('output2:',output2)

输出：

output1: Variable containing:
0.2689
0.7311
[torch.FloatTensor of size 2]

output2: Variable containing:
-1.3133
-0.3133
[torch.FloatTensor of size 2]

以上为个人经验，希望能给大家一个参考，也希望大家多多支持软件开发网。

softmax pytorch

1024 个赞