python算法练习——解空间的穷举搜索与Google方程式
解空间又称为状态空间,是所有可能是解的候选解的集合。穷举是一种在有限的解空间(解空间至少在理论上是有限的)内按照一定的策略进行查找的思想。数学上也把穷举法称为枚举法,就是在一个由有限个元素构成的集合中,将所有元素一一枚举研究的方法。
穷举法的基本思想就是以下两个步骤:
(1)确定问题的解(或状态)的定义,解空间的范围以及正确解的判断条件。
(2)根据解空间的特点选择搜索策略,一一检验解空间中的候选解是否正确,必要时可辅助一些剪枝算法,排除一些明显不可能是正确解的检验过程,提高穷举的效率。
解空间就是全部可能的候选解的一个约束范围,确定问题的解就在这个范围内,将搜索策略应用到这个约束范围就可以找到问题的解。候选解不一定是线性结构,根据问题的类型,解空间的结构可能是线性表、集合、树或者图。有时这个空间内的对象被称为状态,通过对状态的计算和处理,可以间接地得到问题地解,这样的搜索空间也常被理解为状态空间。
要确定解空间,首先要定义问题的解,建立解的数学模型。当候选解或状态之间相互独立,没有关联关系时,可以用线性表,也可以用集合来组织解空间。在很多情况下,候选解或状态之间不独立,存在各种关联关系。不能用一套通用的遍历算法将这些状态都事先确定好,但可以根据状态之间的演化关系,从一种状态推出另一种或几种状态,递归地执行这种状态演化,逐步得到整个状态空间。在这种情况下,解空间通常伴随着搜索算法展开,从一个原始状态开始,逐步扩展至整个解空间。这样的解空间通常被组织成一棵状态树,最终状态就是状态树的叶子节点,从根节点到叶子节点之间的状态转换过程就是问题求解的过程。对于更复杂的情况,需要用图的一些方法组织和搜索解空间,在这种情况下,解空间就是节点和边的关系空间。
穷举解空间的策略就是搜索算法的设计策略。盲目搜索和启发性搜索是两种最常用的搜索策略。盲目搜索就是不带任何假设的穷举搜索。启发性搜索是利用某种策略或计算依据,有目的地搜索,这些策略和依据通常能够加快算法的收敛速度,或者能够划定一个更小的、最有可能出现解的空间并在此空间上搜索。
为了加快算法的求解,通常会在搜索算法中伴随一些剪枝动作。还可以采用限制搜索深度的方法,但为了避免无解或错过最优解,通常只在特定的情况下使用,比如博弈树的搜索。
1.盲目搜索算法
广度优先搜索和深度优先搜索是两种常用的盲目搜索算法,这种搜索算法只根据问题的规模,按照广度优先和深度优先的原则搜索解空间内的每一个状态。广度优先算法需要考虑额外空间的规模,深度优先算法需要做状态循环的判断和避免。
2.启发式搜索算法
启发性搜索需要一些额外信息和操作。如果知道解空间的状态分布呈现正态分布的特征,则可以从分布中间值开始向两边搜索。如果有一个状态评估函数,可以对每个状态节点能演化出解的可能性进行评估,搜索过程中根据这种可能性对待搜索的状态节点排序。如果在某一个层面的搜索能应用贪婪策略,优先选择与贪婪策略符合的状态节点进行搜索,也是一种启发式搜索。
3.剪枝策略
对解空间穷举搜索时,如果有一些状态节点可以根据问题提供的信息明确地被判定为不可能演化出最优解,就可以跳过此状态节点的遍历。难点在于如何找到一个评价方法(估值函数)对状态节点进行评估。此外,在特定搜索策略下会有重复出现的状态节点,需要判断是否是已经处理过的状态节点。
4.搜索算法的评估和收敛
当问题规模太大时,需要对搜索算法进行评估,确定一些收敛原则。
有一个由字符组成的等式:WWWDOT-GOOGLE=DOTCOM,每一个字符代表一个0~9之间的数字,WWWDOT、GOOGLE和DOTCOM都是合法的数字,不能以0开头。找出一组字符和数字之间的对应关系,使它们互相替换,并且能够满足等式。
解决策略穷举的方法就是对每个字母用0~9的数字尝试10次,如果某一次得到的字母和数字的对应关系能够满足减法等式,就输出这一组对应关系。这样的组合共有10!=3628800种。
在数据结构上,需要定义一个可变化的字符元素列表,每个字符元素包含3个属性,分别是字母本身、字母代表的数字以及是否是数字的最高位。
这是一个组合问题,两个字母不能被指定为相同的数字,需要对每个数字做一个标记。
采用递归的方式进行组合枚举,逐个对每个字符进行数字遍历。
对W、G和D是0的情况进行剪枝,从而减少30%的计算判断。利用参数标识字符索引,当参数等于字符个数时,表示所有的字符都已经制指定了对应的数字,调用函数进行结果判断。
import time
# 0:用时127.50秒
# 1:用时51.31秒
USE_MY_ISVALUE = 1
# 字符元素列表
char_item = [
['W', -1, True], ['D', -1, True], ['O', -1, False],
['T', -1, False], ['G', -1, True], ['L', -1, False],
['E', -1, False], ['C', -1, False], ['M', -1, False],
]
# 数字标记
char_value = [
[0, False], [1, False], [2, False], [3, False], [4, False],
[5, False], [6, False], [7, False], [8, False], [9, False]
]
def IsValueVaild(ciItem, cvItem):
'''剪枝评估函数'''
if cvItem[0] == 0:
if USE_MY_ISVALUE:
if ciItem[0] == 'W'or ciItem[0] == 'D'or ciItem[0] == 'G':
return False
else:
return not ciItem[2]
return not cvItem[1]
def MakeIntegerValue(ci, string):
'''获取对应的整数'''
strLen = string.__len__()
res = 0
for i in range(0, strLen, 1):
for item in ci:
if string[i] == item[0]:
res *= 10
res += item[1]
return res
def OnCharListReady(ci):
'''判断数值是否正确'''
minuend = "WWWDOT"
subtrahead = "GOOGLE"
diff = "DOTCOM"
m = MakeIntegerValue(ci, minuend)
s = MakeIntegerValue(ci, subtrahead)
d = MakeIntegerValue(ci, diff)
if (m-s) == d:
print(str(m)+"-"+str(s)+"="+str(d))
def SearchResult(ci, cv, index, callback):
'''搜索结果'''
max_char_count = ci.__len__()
max_number_count = cv.__len__()
if index == max_char_count:
callback(ci)
return
for i in range(0, max_number_count, 1):
if IsValueVaild(ci[index], cv[i]):
cv[i][1] = True # 设置使用标志
ci[index][1] = cv[i][0]
SearchResult(ci, cv, index+1, callback)
cv[i][1] = False # 清除使用标志
if __name__ == '__main__':
print("等式:WWWDOT-GOOGLE=DOTCOM。")
print("解答:")
start = time.clock()
SearchResult(char_item, char_value, 0, OnCharListReady)
end = time.clock()
print("使用了: %f s" % (end - start))
运行
在fish终端中的运行结果如下:
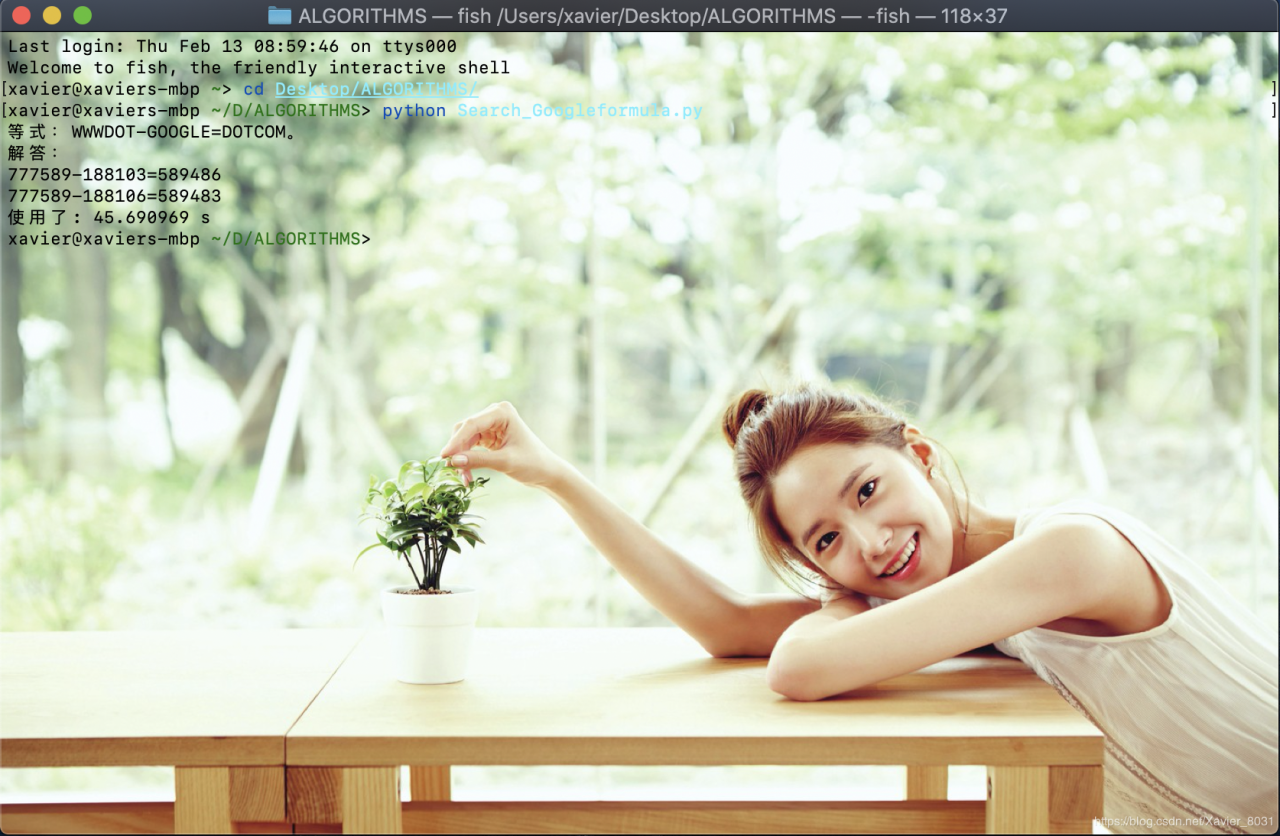
感谢广大网友。
主要参考内容:
[1]《算法的乐趣》——王晓华
[2]https://blog.csdn.net/yannanxiu/article/details/51758360
作者:Xavier_8031