python算法深入理解风控中的KS原理
一、业务背景
二、直观理解区分度的概念
三、KS统计量的定义
四、KS计算过程及业务分析
KS常用的计算方法:
上标指标计算逻辑:
五、风控中选择KS的原因
例1:模糊性
例2:连续性
一、业务背景在金融风控领域,常常使用KS指标来衡量评估模型的区分度(discrimination),这也是风控模型最为追求的指标之一。下面将从区分度概念、KS计算方法、业务指导意义、几何解析、数学思想等角度,对KS进行深入剖析。
二、直观理解区分度的概念在数据探索中,若想大致判断自变量x对因变量y有没有区分度,常会将样本分为正负来观察变量的分布差异。那么,如何判断自变量是有用的?直观理解,如果两个分布的重叠部分越小,代表正负样本的差异性越大,自变量就能更好的将正负样本区分开来。具体如图1所示。
打个比方,想象这个变量就是一双手,把这个分布往两边拉开。这双手的力量越大,两个概率分布间隔就越远,说明变量区分性就越强。
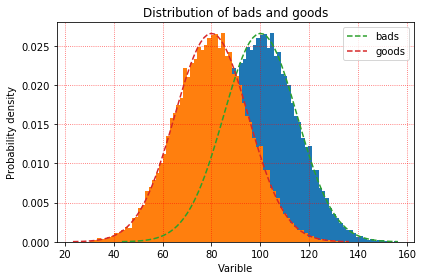
图1 - 正负样本分布差异对比
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
mu = 100 # mean of distribution
sigma = 15 # standard deviation of distribution
x = mu + sigma * np.random.randn(20000)
num_bins = 80
fig, ax = plt.subplots()
# the histogram of the data
n, bins, patches = ax.hist(x, num_bins, density=1)
n1, bins1, patches1 = ax.hist(x - 20, num_bins, density=1)
# add a 'best fit' line
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
y1 = ((1 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
ax.plot(bins, y, '--', label = 'bads')
ax.plot(bins1, y, '--', label = 'goods')
ax.set_xlabel('Varible')
ax.set_ylabel('Probability density')
ax.set_title('Distribution of bads and goods')
fig.tight_layout()
plt.grid(True,linestyle = ':', color = 'r', alpha = 0.7)
plt.legend()
plt.show()
三、KS统计量的定义
KS(Kolmogorov-Smirnov)统计量由两位苏联科学家A.N.Kolmogorov和N.V.Smirnov提出。
在风控中KS通常用于评估模型区分度,区分度越大,说明模型风险排序能力越强。
KS是基于经验累积分布函数(Emporical Cumulative Distribution Function,ecdf)建立的
四、KS计算过程及业务分析 KS常用的计算方法:step1:对变量进行分箱(binning),可以选择等频、等距或者自定义距离。
step2:计算每个分箱区间的好样本数(goods)与坏样本数(bads)。
step3:计算每个分箱区间内累计好客户占总好客户比值(cum_good_rate)和累计坏客户占总坏客户比值(cum_bad_rate)。
step4:计算每个分箱区间累计坏客户占比与累计好客户占比的绝对值,得到KS曲线,也就是:
step5:在这些绝对值中取最大值,得到此变量的最终KS值。
为了便于理解,以具体的数据展示上述过程:

表1 - KS计算过程表
上标指标计算逻辑:从上表中可以得到以下信息:
1.模型分数越高,逾期率越低,因此低分段bad_rate相对于高分段更高,cum_bad_rate曲线增长速率会比cum_good_rate更快。cum_bad_rate曲线在cum_good_rate曲线上方。
2.每个分箱样本数量基本相同,说明是等频分箱。
3.如将cutoff限定为0.65,则其cum_bad_rate为82.75%,表示有82.75%的坏客户会被拒绝,但同时cum_good_rate为29.69%,表示同时会有29.69%的好客户会被拒绝。
4.根据bad_rate的变化趋势,模型的排序性很好。如果是A卡,对排序性的要求会更高,因为需要根据风险等级对用户风险定价。
5.模型的KS达到53.1%,区分度较强,这是最理想的状态,实际业务应用中需要根据预设条件权衡通过率与坏账率的关系,一般cutoff不会选在理想值处,因此可知,KS是区分度的上限。
6.对于A卡来说,通常KS很难达到52%,因此,若上表数据为A卡结果,需要进一步确认模型是否发生过拟合。
需要进一步指出的是,KS是在放贷样本上评估的,放贷样本对于全量样本永远是有偏的。对于裸奔风控系统,偏差会很小;反之如果风控系统做的越好,偏差就会越大。因此KS不仅仅只是一个数字,其背后蕴藏的很多原因,需要结合业务进行具体分析。
当KS不佳时,为了达到预期目的,可进行以下校验:
1.检验入模变量是否已被策略使用,使用重复变量会导致模型无法命中本应被命中的坏客户,导致模型效果下降。
2.检验训练样本与验证样本之间的客群差异是否明显,其中包括时间分布,某些特征分布、特殊特征命中情况等。
3.开发对目标场景更具针对性的新特征,比如税务场景,在进行特征衍生时,更加关注税务指标;如识别长期风险,就使用强金融属性变量,对于欺诈风险,就使用一些短期的负面变量。
4.分群建模,但须考虑稳定性与差异性,防止过拟合。
5.坏客户分析,试图通过个性推共性。
对表1数据进行可视化,便得到KS曲线,主要使用到最后三列数据,即cum_good_rate、cum_bad_rate和KS,具体代码和图像如下:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
cum_good_rate = np.array([0.00,0.05,0.12,0.20,0.30,0.41,0.53,0.71,0.86,1.00])
cum_bad_rate = np.array([0.26,0.45,0.59,0.72,0.83,0.90,0.97,0.99,1.00,1.00])
x = np.linspace(0, 1, 10)
plt.plot(x, cum_good_rate, label = 'cum_good_rate')
plt.plot(x, cum_bad_rate, label = 'cum_bad_rate')
plt.plot(x, cum_bad_rate - cum_good_rate, label = 'KS')
plt.title('KS Curve', fontsize = 16)
plt.grid(True,linestyle = ':', color = 'r', alpha = 0.7)
plt.axhline(y = 0.53, c = 'r', ls = '--', lw = 3) #绘制平行于x轴的水平参考线
plt.axvline(x = 0.43, c = 'r', ls = '--', lw = 3) #绘制平行于y轴的垂直参考线
plt.legend()
plt.show()
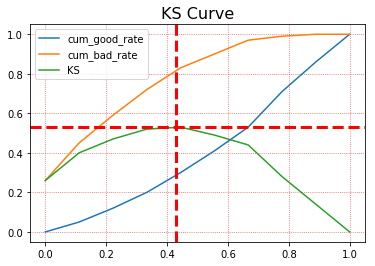
图2 - KS曲线
至此,我们已经了解了KS的计算的基本流程、评价标准、业务指导意义和优化思路,接下来有几个问题:
1.为什么风控中常用KS来评价模型效果,而不是使用准确率、召回率等?
2.最大KS只是一个宏观的结果,那么在不同的cutoff下取到max,模型效果有何差异?
3.一般情况下,KS越大越好,但为什么通常认为高于75%的KS就不可靠了?
五、风控中选择KS的原因风控建模过程中,常把样本标签分为GBIX四类,其中:G=Good(好人,标记为0),B=Bad(坏人,标记为1),I=Indeterminate(不定,未进入表现期),X=Exclusion(排斥,异常样本)。
需要指出的是,Good与Bad之间的定义往往是模糊的、连续的,依赖于实际业务需求。这里举两个例子帮助理解:
例1:模糊性对于12期信贷产品,如果设定表现期为前6期,S6D15(前6期中,任意一期逾期超15天)就是1,否则为0;但后来如果把表现期调整为3期,那么对于**“前3期都正常还款,但4~6期才发生逾期并超过15天”**的这部分样本,原本所定义的label就从1变成了0.因此业务需求不同,导致标签的定义不是绝对的。所以说,好坏样本定义一定要根据实际业务需求来,要在对业务进行充分理解与分析的基础上进行确定,而不是拍脑袋而为之。
例2:连续性定义首期逾期超30天为1,否则为0。但是,逾期29天与逾期31天的用户之间其实并没有不可跨越的硬间隔,逾期29天的用户可能会进一步恶化为逾期31天。
由于逾期严重程度定义本身就带有一定的主观色彩,我们很难说逾期天数差几天有多少本质差异,所以哪怕我们为了转化为分类问题做了硬性的1和0的界限定义,但业务上理解还是一个连续问题。
因此,在风控中,y的定义并不是非黑即白(离散型),而用概率分布(连续型)衡量或许更合理。
那么,为什么选择KS指标呢?KS倾向于从概率角度衡量正负样本之间的差异,正是因为正负样本之间的模糊性与连续性,所以KS也是一条连续曲线。但最终为什么取一个最大值,主要原因是提取KS曲线中的的一个显著特征,从而便于相互比较。
以上就是python算法深入理解风控中的KS原理的详细内容,更多关于python算法风控KS原理的资料请关注软件开发网其它相关文章!