Python可视化神器pyecharts之绘制箱形图
箱形图
概念
用处
箱形图系列模板
第一个箱形图
复杂一点的图例
箱形图 概念后面的图形都是一些专业的统计图形,当然也会是我们可视化的对象。
箱形图(Box-plot)又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用,常见于 品质管理。它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比 较。箱线图的绘制方法是:先找出一组数据的上边缘、下边缘、中位数和两个四分位数;然后, 连接两个四分位数画出箱体;再将上边缘和下边缘与箱体相连接,中位数在箱体中间。
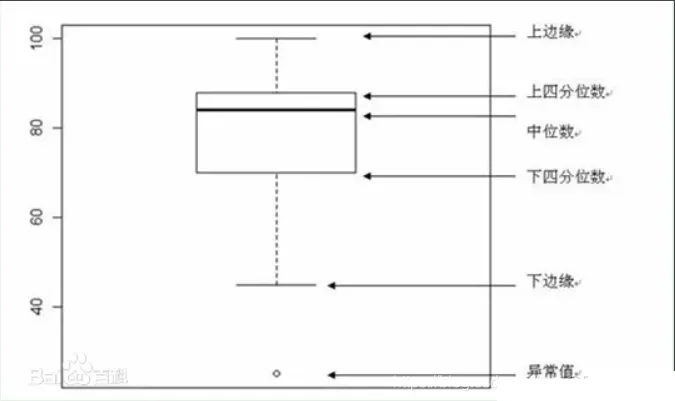
1.直观明了地识别数据批中的异常值
上文讲了很久的识别异常值,其实箱线图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不会影响箱形图的数据形状,箱线图识别异常值的结果比较客观。由此可见,箱线图在识别异常值方面有一定的优越性。
2.利用箱线图判断数据批的偏态和尾重
对于标准正态分布的样本,只有极少值为异常值。异常值越多说明尾部越重,自由度越小(即自由变动的量的个数);
而偏态表示偏离程度,异常值集中在较小值一侧,则分布呈左偏态;异常值集中在较大值一侧,则分布呈右偏态。
3.利用箱线图比较几批数据的形状
同一数轴上,几批数据的箱线图并行排列,几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。如上图,可直观得看出第三季度各分公司的销售额大体都在下降。
箱形图系列模板 第一个箱形图说实话这类图形的绘制,如果不懂专业的知识可能也无法理解,对于如何深层次的理解这个图形的具体含义,请移步到其他专栏,我会详细介绍,这里就不做过多的解释了。
from pyecharts import options as opts
from pyecharts.charts import Boxplot
v1 = [
[850, 740, 900, 1070, 930, 850, 950, 980, 980, 880, 1000, 980],
[960, 940, 960, 940, 880, 800, 850, 880, 900, 840, 830, 790],
]
v2 = [
[890, 810, 810, 820, 800, 770, 760, 740, 750, 760, 910, 920],
[890, 840, 780, 810, 760, 810, 790, 810, 820, 850, 870, 870],
]
c = Boxplot()
c.add_xaxis(["expr1", "expr2"])
c.add_yaxis("A", c.prepare_data(v1))
c.add_yaxis("B", c.prepare_data(v2))
c.set_global_opts(title_opts=opts.TitleOpts(title="标题"))
c.render("简单示例.html")
print(c.prepare_data(v1))

import pyecharts.options as opts
from pyecharts.charts import Grid, Boxplot, Scatter
y_data = [
[
850,
740,
900,
1070,
930,
850,
950,
980,
980,
880,
1000,
980,
930,
650,
760,
810,
1000,
1000,
960,
960,
],
[
960,
940,
960,
940,
880,
800,
850,
880,
900,
840,
830,
790,
810,
880,
880,
830,
800,
790,
760,
800,
],
[
880,
880,
880,
860,
720,
720,
620,
860,
970,
950,
880,
910,
850,
870,
840,
840,
850,
840,
840,
840,
],
[
890,
810,
810,
820,
800,
770,
760,
740,
750,
760,
910,
920,
890,
860,
880,
720,
840,
850,
850,
780,
],
[
890,
840,
780,
810,
760,
810,
790,
810,
820,
850,
870,
870,
810,
740,
810,
940,
950,
800,
810,
870,
],
]
scatter_data = [650, 620, 720, 720, 950, 970]
box_plot = Boxplot()
box_plot = (
box_plot.add_xaxis(xaxis_data=["expr 0", "expr 1", "expr 2", "expr 3", "expr 4"])
.add_yaxis(series_name="", y_axis=box_plot.prepare_data(y_data))
.set_global_opts(
title_opts=opts.TitleOpts(
pos_left="center", title="Michelson-Morley Experiment"
),
tooltip_opts=opts.TooltipOpts(trigger="item", axis_pointer_type="shadow"),
xaxis_opts=opts.AxisOpts(
type_="category",
boundary_gap=True,
splitarea_opts=opts.SplitAreaOpts(is_show=False),
axislabel_opts=opts.LabelOpts(formatter="expr {value}"),
splitline_opts=opts.SplitLineOpts(is_show=False),
),
yaxis_opts=opts.AxisOpts(
type_="value",
name="km/s minus 299,000",
splitarea_opts=opts.SplitAreaOpts(
is_show=True, areastyle_opts=opts.AreaStyleOpts(opacity=1)
),
),
)
.set_series_opts(tooltip_opts=opts.TooltipOpts(formatter="{b}: {c}"))
)
scatter = (
Scatter()
.add_xaxis(xaxis_data=["expr 0", "expr 1", "expr 2", "expr 3", "expr 4"])
.add_yaxis(series_name="", y_axis=scatter_data)
.set_global_opts(
title_opts=opts.TitleOpts(
pos_left="10%",
pos_top="90%",
title="upper: Q3 + 1.5 * IQR \nlower: Q1 - 1.5 * IQR",
title_textstyle_opts=opts.TextStyleOpts(
border_color="#999", border_width=1, font_size=14
),
),
yaxis_opts=opts.AxisOpts(
axislabel_opts=opts.LabelOpts(is_show=False),
axistick_opts=opts.AxisTickOpts(is_show=False),
),
)
)
grid = (
Grid(init_opts=opts.InitOpts(width="1200px", height="600px"))
.add(
box_plot,
grid_opts=opts.GridOpts(pos_left="10%", pos_right="10%", pos_bottom="15%"),
)
.add(
scatter,
grid_opts=opts.GridOpts(pos_left="10%", pos_right="10%", pos_bottom="15%"),
)
.render("第一个箱形图.html")
)

其实对于这个图形的绘制我个人觉得掌握好一定技巧,绘制图形并不难,主要是你要知道一定数据分析方法,不然空谈数据可视也是枉然。
到此这篇关于Python可视化神器pyecharts之绘制箱形图的文章就介绍到这了,更多相关Python绘制箱形图内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!