python机器学习入门案例——基于SVM分类器的鸢尾花分类(附完整代码)

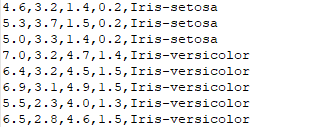
数据集样式:

import numpy as np
from matplotlib import colors
from sklearn import svm
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl
具体模块下载如果出现问题可见博客:
手把手教你进行pip换源
(1) 从指定路径下加载数据,将字符串转为整型
(2) 对加载的数据进行数据分割,x_train,x_test,y_train,y_test分别表示训练集特征、训练集标签、测试集特征、测试集标签
(3) 一部分数据用于构建模型,叫做训练数据,另一部分用于评估模型性能,叫做测试数据。利用scikit-learn中的train_test_split函数可以实现这个功能
# 将字符串转为整型,便于数据加载
def iris_type(s):
it = {b'Iris-setosa':0, b'Iris-versicolor':1, b'Iris-virginica':2}
return it[s]
# 加载数据
data_path = 'iris.data' # 数据文件的路径
data = np.loadtxt(data_path, # 数据文件路径
dtype=float, # 数据类型
delimiter=',', # 数据分隔符
converters={4: iris_type}) # 将第5列使用函数iris_type进行转换
# 数据分割
x, y = np.split(data, # 要切分的数组
(4,), # 沿轴切分的位置,第5列开始往后为y
axis=1) # 代表纵向分割,按列分割
x = x[:, 0:2] # 在X中我们取前两列作为特征,为了后面的可视化。x[:,0:4]代表第一维(行)全取,第二维(列)取0~2
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, # 所要划分的样本特征集
y, # 所要划分的样本结果
random_state=1, # 随机数种子
test_size=0.3) # 测试样本占比
SVM分类器构建
# SVM分类器构建
def classifier():
clf = svm.SVC(C=0.5, #误差项惩罚系数,默认值是1
kernel='linear', #线性核
decision_function_shape='ovr') #决策函数
return clf
# 定义模型:SVM模型定义
clf = classifier()
C为误差项惩罚系数,默认值是1,当C越大,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增大,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。 C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
kernel='linear':线性核
kenrel='rbf':高斯核
decision_function_shape:决策函数
'ovr'时,为one v rest,即一个类别与其他类别进行划分
为'ovo'时,为one v one,即将类别两两之间进行划分,用二分类的方法模拟多分类的结果。
模型训练
def train(clf,x_train,y_train):
clf.fit(x_train, #训练集特征向量
y_train.ravel()) #训练集目标值
# 训练SVM模型
train(clf,x_train,y_train)
模型评估
计算均值
# 并判断a b是否相等,计算acc的均值
def show_accuracy(a, b, tip):
acc = a.ravel() == b.ravel()
print('%s Accuracy:%.3f' %(tip, np.mean(acc)))
打印训练集和测试集的准确率
def print_accuracy(clf,x_train,y_train,x_test,y_test):
#分别打印训练集和测试集的准确率 score(x_train,y_train):表示输出x_train,y_train在模型上的准确率
print('trianing prediction:%.3f' %(clf.score(x_train, y_train)))
print('test data prediction:%.3f' %(clf.score(x_test, y_test)))
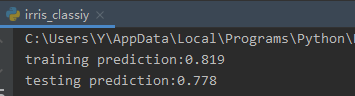
训练集的准确率:trianing prediction:0.819
测试集的准确率:testing prediction:0.778
# predict()表示对x_train样本进行预测,返回样本类别
show_accuracy(clf.predict(x_train), y_train, 'traing data')
show_accuracy(clf.predict(x_test), y_test, 'testing data')
训练集预测结果:training data Accuracy:0.819
测试集预测结果:testing data Accuracy:0.778
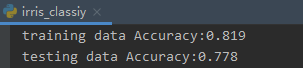
可见原始结果与预测结果是一样的
计算决策函数的值 #计算决策函数的值,表示x到各分割平面的距离
print('decision_function:\n', clf.decision_function(x_train))
模型评估
print_accuracy(clf,x_train,y_train,x_test,y_test)
输出的值
decision_function:
[[-0.30200388 1.26702365 2.28292526]
[ 2.1831931 -0.19913458 1.06956422]
[ 2.25424706 0.79489006 -0.20587224]
[ 2.22927055 0.98556708 -0.22777916]
[ 0.95815482 2.18401419 -0.17375192]
[ 2.23120771 0.84075865 -0.19144453]
[ 2.17327158 -0.14884286 0.92795057]
[-0.28667175 1.11372202 2.28302495]
[-0.27989264 1.21274017 2.25881762]
[-0.29313813 1.24442795 2.2732035 ]
[-0.27008816 1.2272086 2.22682127]
[-0.25981661 2.21998499 1.20479842]
[-0.17071168 0.99542159 2.17180911]
[-0.30018876 1.25829325 2.2829419 ]
[-0.17539342 2.15368837 1.06772814]
[ 2.25702986 0.81715893 -0.22763295]
[-0.23988847 2.23286001 1.06656755]
[-0.26915223 2.23333222 1.21679709]
[ 2.22927055 0.98556708 -0.22777916]
[ 2.2530903 0.85932358 -0.2359772 ]
[-0.26740532 1.20784059 2.23528903]
[ 2.26803658 0.80468578 -0.24299359]
[-0.24030826 1.18556963 2.19011259]
[-0.25881807 1.17240759 2.23535197]
[-0.27273902 1.20332527 2.24866913]
[-0.20956348 2.19674141 1.06726512]
[-0.26556065 1.16490628 2.24871607]
[-0.22965507 1.17870942 2.17146651]
[ 2.25807657 -0.22526231 0.80881977]
[-0.27322701 2.25917947 1.17077691]
[-0.26638767 1.21631409 2.22685842]
[-0.26740532 1.20784059 2.23528903]
[-0.12135744 2.22922779 0.79343961]
[-0.2365929 1.12219635 2.21706342]
[-0.21558048 2.22640865 0.92573306]
[ 2.22344499 -0.19955645 0.88288227]
[ 2.22671228 0.93600592 -0.21794279]
[ 2.26578978 -0.24701281 0.82742467]
[-0.26556065 1.16490628 2.24871607]
[ 2.26204658 0.89725133 -0.25453765]
[-0.2518152 2.22343258 1.17120859]
[-0.27340098 1.23624732 2.22678409]
[-0.21624631 2.17118121 1.14723861]
[ 2.22874494 -0.17513313 0.8269183 ]
[ 2.2211989 0.87213971 -0.19151045]
[-0.23391072 2.21566697 1.11400955]
[ 2.22671228 0.93600592 -0.21794279]
[-0.29609931 1.25285329 2.27596663]
[-0.25476857 1.20746943 2.20485252]
[-0.29672783 1.24461331 2.28083131]
[-0.27578664 1.21663499 2.24864564]
[-0.28091389 2.25930846 1.21661886]
[-0.21369288 1.05233452 2.20512234]
[-0.27669555 1.12529292 2.27023906]
[-0.16942442 2.17056098 0.99533295]
[ 2.24933086 -0.25468768 1.0709247 ]
[-0.23391072 2.21566697 1.11400955]
[ 2.18638944 1.20994285 -0.24936796]
[-0.22656825 2.23557826 0.92551338]
[-0.27989264 1.21274017 2.25881762]
[ 2.24156015 0.83211053 -0.20597859]
[-0.28390119 1.23920595 2.25400509]
[ 2.24837463 0.81114157 -0.20592544]
[ 2.25702986 0.81715893 -0.22763295]
[-0.22765797 1.07419821 2.21710769]
[-0.18996302 2.19089984 0.99497945]
[-0.27357394 1.19278157 2.25408746]
[ 2.23355717 0.86019975 -0.2060317 ]
[ 2.25277813 -0.21394322 0.80875361]
[-0.18611572 1.10670475 2.14746524]
[ 2.25454797 0.88341904 -0.24307373]
[-0.23391072 2.21566697 1.11400955]
[ 2.23794605 0.91585392 -0.22774264]
[-0.26740532 1.20784059 2.23528903]
[ 2.0914977 1.20089769 -0.21820392]
[ 2.25962348 0.84878847 -0.24304703]
[-0.25213485 1.16423702 2.22696973]
[ 2.26725005 0.88232062 -0.25923379]
[-0.14201734 2.14344591 0.99568721]
[ 2.25731 0.95572321 -0.25455798]
[-0.22656825 2.23557826 0.92551338]
[-0.19708433 2.25161696 0.79328185]
[ 2.23957622 0.81769302 -0.19137855]
[ 2.21575566 1.0173258 -0.21798639]
[ 1.02668315 2.21468275 -0.21824732]
[ 2.27472592 0.77777882 -0.24294008]
[-0.21624631 2.17118121 1.14723861]
[-0.24730284 1.20252603 2.19004536]
[ 2.24156015 0.83211053 -0.20597859]
[-0.27273902 1.20332527 2.24866913]
[-0.19455078 2.17814555 1.06749683]
[-0.28027257 2.2623408 1.20447285]
[-0.28054312 1.20372124 2.26304729]
[-0.23391072 2.21566697 1.11400955]
[ 2.17896853 -0.12686338 0.8824238 ]
[ 2.19820639 1.04471124 -0.20619077]
[-0.26313706 2.23602532 1.18984329]
[-0.25331913 2.21599142 1.18997806]
[-0.28966527 1.23403227 2.27016072]
[-0.23157808 2.22314802 1.06680048]
[-0.26533811 1.22371567 2.21684157]
[-0.25751543 1.18608093 2.22693265]
[-0.27562627 2.24825903 1.21670804]
[-0.27273902 1.20332527 2.24866913]
[ 2.22671228 0.93600592 -0.21794279]]
模型使用
沿着新的轴加入一系列数组
grid_test = np.stack((x1.flat, x2.flat), axis=1)
print('grid_test:\n', grid_test)
输出结果:
沿着新的轴加入一系列数组:
[[4.3 2. ]
[4.3 2.0120603]
[4.3 2.0241206]
...
[7.9 4.3758794]
[7.9 4.3879397]
[7.9 4.4 ]]
得到输出样本到决策面的距离
z = clf.decision_function(grid_test)
print('样本到决策面的距离:\n', z)
结果:
样本到决策面的距离:
[[ 2.17689921 1.23467171 -0.25941323]
[ 2.17943684 1.23363096 -0.25941107]
[ 2.18189345 1.23256802 -0.25940892]
...
[-0.27958977 0.83621535 2.28683228]
[-0.27928358 0.8332275 2.28683314]
[-0.27897389 0.83034313 2.28683399]]
得到预测分类值
grid_hat = clf.predict(grid_test) # 预测分类值 得到【0,0.。。。2,2,2】
print('预测分类值:\n', grid_hat)
grid_hat = grid_hat.reshape(x1.shape) # reshape grid_hat和x1形状一致
结果:
预测分类值:
[0. 0. 0. ... 2. 2. 2.]
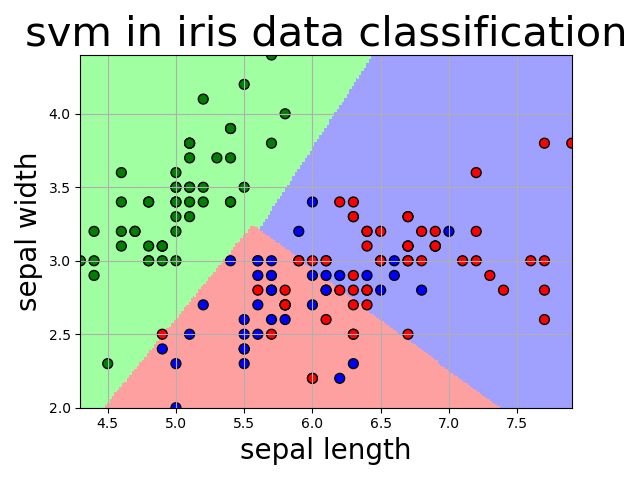
画出模型分类图
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark) # 样本点
plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolor='none', zorder=10) # 测试点
plt.xlabel(iris_feature[0], fontsize=20)
plt.ylabel(iris_feature[1], fontsize=20)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title('svm in iris data classification', fontsize=30)
plt.grid()
plt.show()
 原创文章 54获赞 107访问量 1万+
关注
私信
展开阅读全文
原创文章 54获赞 107访问量 1万+
关注
私信
展开阅读全文
作者:ywsydwsbn