Python判断一个正整数是否为素数的算法
先定义一个有序列表,作为素数池,这样多次操作的时候可以直接用里面的素数作为取模的除数,以避免用冗余的合数来运算和重复性的运算:
primePool = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,79,83,89,97,101,103,107,109,113]
定义素数判断函数
def isPrime(num):
if num in primePool:
return True
sq = math.sqrt(num)
p=2
for m in primePool: #先从素数池中找
p = m
if math.fmod(num,m)==0:
print('Divider:',m)
return False
if p > sq:
return True
p = p+2
while p<=sq:
if isPrime(p):
primePool.append(p)#素数池维护
if math.fmod(num,p)==0:
print('Divider:',p)
return False
p = p+2 #以2为步长,避免无用的偶数判断
#primePool.append(num)
'''
如果num是素数暂时不将其放入有序素数池中,因为还要判断并添加从p到num之间的所有素数。对于本函数而言是个较大的计算量。
'''
return True
运行示例:
isPrime(17947)
结果:
Divider: 5 # p==115时,p被5整除
Divider: 3 # p==117时,p被3整除
Divider: 7 # p==119时,p被7整除
Divider: 11 # p==121时,p被11整除
Divider: 3 # p==123时,p被3整除
Divider: 5 # p==125时,p被5整除
Divider: 3 # p==127时,向素数池中添加127;然后判断p==129时,被3整除
Divider: 131 # p==131时,向素数池中添加131;
False # num被131整除
时间复杂度估算为:
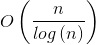
它与素数的密度分布有关。而且随着素数池primePool的逐渐积累,函数的效率也会显著提升。
作者:超级大超越