python绘制超炫酷动态Julia集示例
前言
Mandelbrot集
无限缩放
Julia集
前言此Julia非彼Julia,指的是对于某复数 c c c,使得迭代式 f ( z ) = z 2 + c f(z)=z^2+c f(z)=z2+c收敛的复数 z z z的集合。例如,当 c = 0 c=0 c=0时,那么其收敛区间为 z 2 < 1 z^2<1 z2<1的单位圆,对应的 c c c的Julia集便是 cos θ + i sin θ \cos\theta+i\sin\theta cosθ+isinθ。
Mandelbrot集特别地,当 c = z c=z c=z的初始值时,符合收敛条件的 z z z的便构成大名鼎鼎的Mandelbrot集

在上图中,颜色表示该点的发散速度,可以理解为开始发散时迭代的次数。其生成代码也非常简单,唯一需要注意的是,由于使用了大量的矩阵运算,故使用了cupy,如果电脑没装cuda,只需将所有的cp改为np即可。
# 这些代码会在后面的程序中反复调用,不再说明
import numpy as np
import time
import matplotlib.pyplot as plt
import cupy as cp
#生成z坐标 x0,y0 为起始点, nx,ny为点数, delta为点距
def genZ(x0, y0, nx, ny, delta):
real, img = cp.indices([nx,ny])*delta
real += x0
img += y0
return real.T+img.T*1j
#获取Julia集,n为迭代次数,m为判定发散点,大于1即可
def getJulia(z,c,n,m=2):
t = time.time()
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
for i in range(n):
absz = cp.abs(z)
z[absz>m]=0#对开始发散的点置零
c[absz>m]=0
out[absz>m]=i#记录发散点的发散速度
z = z*z + c
print("time:",time.time()-t)
return out
z1 = genZ(-2,-1.5,1000,1000,0.003)
mBrot = getJulia(z1,z1,50)
plt.imshow(mBrot.get(), cmap=plt.cm.jet)
plt.show()
如果对其生成过程感兴趣,那么可以观察一下随着迭代次数的增加,图像的变化情况
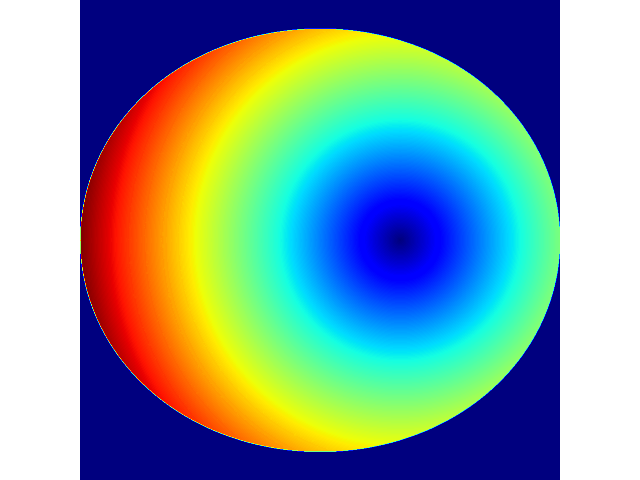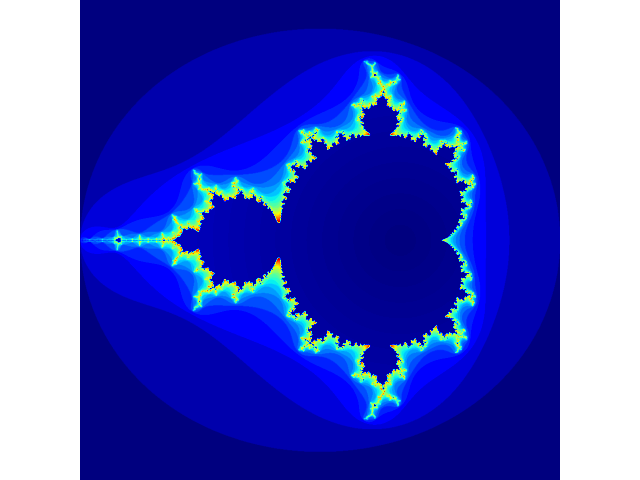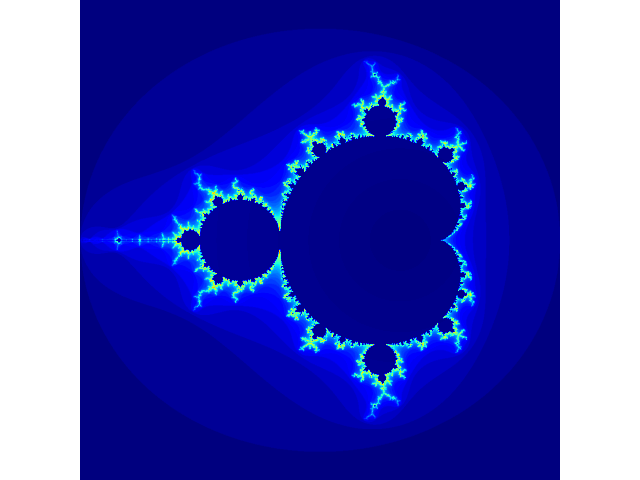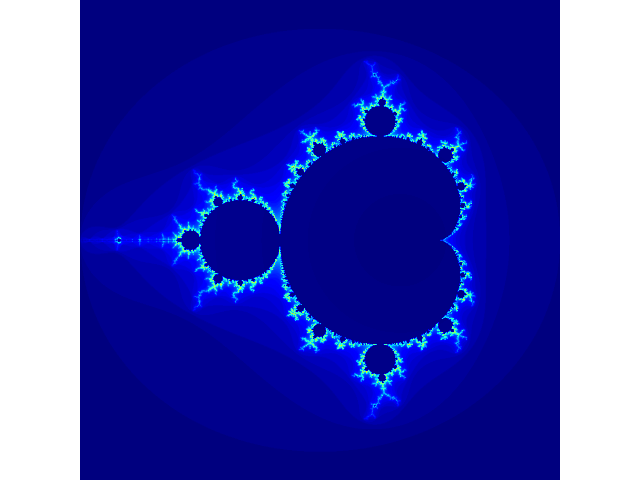
代码如下。
from matplotlib import animation
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
def getJulias(z,c,n,m=2):
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
J = []
for i in range(n):
z = z*z + c
absz = cp.abs(z)
z[absz>m]=0#对开始发散的点置零
c[absz>m]=0
out[absz>m]=i#记录发散点的发散速度
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
J.append([im])
return J
N = 75 #迭代次数
z1 = genZ(-2,-1.5,1000,1000,0.003)
J = getJulias(z1,z1,N)
ani = animation.ArtistAnimation(fig, J, interval=50, blit=True,repeat_delay=1000)
plt.show()
ani.save('julias.gif',writer='imagemagick')
无限缩放
Mandelbrot集的分形特征意味着我们所生成的图片可以无限放大,但是受到栅格化尺寸的影响,手动的放大并不会更改其真实尺寸,
为了照顾观感,将缩放中心作为图像的中心,所以对genZ函数进行修改。如果选取(-0.75,-0.2)作为缩放中心,则其变化如下

代码为
from matplotlib import animation
# 生成z坐标 xy=np.array([xc,yc]) 为起始点,
# nxy=np.array([nx,ny])为点数, delta为点距
def genZbyCenter(xy,nxy,delta):
x0, y0 = xy-np.array(nxy)*delta/2
return genZ(x0,y0,*nxy,delta)
mBrots = []
xy = [-0.75,-0.2]
nxy = [1000,1000]
delta0 = 0.003 #初始宽度
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
for n in range(50):
z1 = genZbyCenter(xy,nxy,1.1**(-n)*delta0)
out = getJulia(z1,z1,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50, blit=True)
plt.show()
ani.save('zoom.gif',writer='imagemagick')
Julia集
如果更改c的值,那么就能得到一个变化着的Julia集,例如,下面选取一条直线
y = x y=x y=x
上面的Julia集,效果如图所示

代码为
z1 = genZ(-2,-1.5,1000,1000,0.003)
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
mBrots = []
for x in np.arange(0.5,1,0.01):
c = x + x*1j
out = getJulia(z1,c,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50)
plt.show()
ani.save('julia.gif',writer='imagemagick')
到此这篇关于python绘制超炫酷动态Julia集示例的文章就介绍到这了,更多相关python绘制动态Julia集内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!