PAT A1079.(两种解法)Total Sales of Supply Chain
题意
作者:Juicy B
(原题为英文,这里直接介绍题目大意,节省大家读题的时间)
给出一棵供销树,树根唯一。在树根(根结点)处货物的价格为p,然后从根结点开始每往子结点走一层,货物的价格就在上一个结点价格的基础上增加 r%。现在给出每个叶子结点的货物量,求它们的价格之和。
假设有一棵供销树如下:
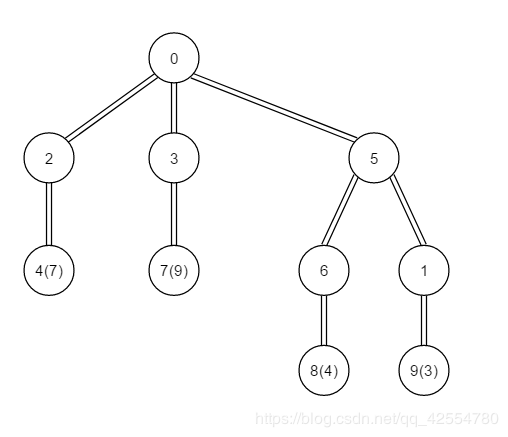
输入样例和样例解释如下,请对照上图进行理解:
10 1.80 1.00 //结点总个数n、货物销售单价p、价格上涨的增量r
3 2 3 5 //结点0的子结点个数为3,分别为2、3、5
1 9 //结点1的子结点个数为1,子结点为9,其他同理
1 4
1 7
0 7 //结点4子结点个数为0(即叶子结点),货物量为7,其他同理
2 6 1
1 8
0 9
0 4
0 3
输出样例
输出为所有叶子结点货物的价格总和,即:
1.80 × (7 + 9) × (1 + 0.01) ² + 1.80 × (4 + 3) × (1 + 0.01) ³ = 42.4(保留一位小数)。
42.4
思路
方法一: 广度优先搜索(非递归)
定义结构体 node,记录每个结点的深度depth、货物量good_nums以及所有子结点(由于每个结点的子结点个数不确定,故可以将各自的子结点存放在vector容器children里)。利用叶子结点的子结点个数为0的性质,可以找出所有叶子结点,再根据各叶子结点的深度以及对应的货物销售量,还有货物的单价,就可以算出总价格。
方法二:深度优先搜索(递归)
同样也要定义结构体node,与方法一的 node的不同之处在于少了depth,这是因为该方法将depth作为递归函数的参数直接参与递归,通过设置根结点的depth为0,每次调用递归函数时都让depth加1,就可以使得使每一个子结点的深度都比其父结点多1,从而准确计算出每一个结点的深度。其他地方与方法一类似。
方法一:广度优先搜索(BFS)
#include
#include
#include
#include
#include
using namespace std;
//这里注意 maxn要满足题目要求,否则会出现段错误(测试数据过大导致数组越界)
const int maxn = 100000;
int n;
struct node
{
int depth;
int good_nums;
vector children;
}nodes[maxn];
void BFS(node* root)
{
//队列 q用来存储每一个结点的地址
queue q;
//将根结点的地址送入队列
q.push(root);
while(!q.empty())
{
//队列 q非空,则读取队首结点地址
node* tmp = q.front();
//读取完队首地址之后要将其弹出
q.pop();
for (int i = 0; i children.size(); i++)
{
//读取所有子结点,每一个子结点的深度都比其父节点多1
nodes[tmp->children[i]].depth = tmp->depth + 1;
//将每个子结点的地址送入队列
q.push(nodes + tmp->children[i] );
}
}
}
int main()
{
int k, child; //每个结点的子结点个数、子结点编号
double p, r; //单价、价格增量
cin>>n>>p>>r;
for(int i = 0; i >k;
if(k == 0)
{
//是叶子结点则输入货物量
cin>>nodes[i].good_nums;
}
else
{
//不是叶子结点则输入子结点编号
for (int j = 0; j >child;
nodes[i].children.push_back(child);
}
}
}
//根结点(编号0)的深度初始化为0
nodes[0].depth = 0;
BFS(nodes);
double price = 0;
for(int i = 0; i < n; i++)
{
//子结点数为 0,说明是叶子结点,计算它们的货物总价格
if(nodes[i].children.size() == 0)
{
price += p * nodes[i].good_nums * pow( (1 + r / 100), nodes[i].depth );
}
}
//设置输出结果保留小数点后 1位
cout<<fixed<<setprecision(1)<<price<<endl;
return 0;
}
方法二:深度优先搜索(DFS)
#include
#include
#include
#include
using namespace std;
const int maxn = 100000;
struct node
{
int good_nums;
vector children;
}nodes[maxn];
int n;
double p, r, price = 0;
void DFS(int index, int depth)
{
//递归边界:子结点个数为0,说明是叶子结点,计算它们的货物总价格
if(nodes[index].children.size() == 0)
{
price += p * nodes[index].good_nums * pow( (1 + r / 100 ), depth );
}
for(int i = 0; i >n>>p>>r;
for(int i = 0; i >k;
if(k == 0)
{
cin>>nodes[i].good_nums;
}
else
{
for (int j = 0; j >child;
nodes[i].children.push_back(child);
}
}
}
//根结点的编号和深度均为 0
DFS(0, 0);
cout<<fixed<<setprecision(1)<<price<<endl;
return 0;
}
提交结果
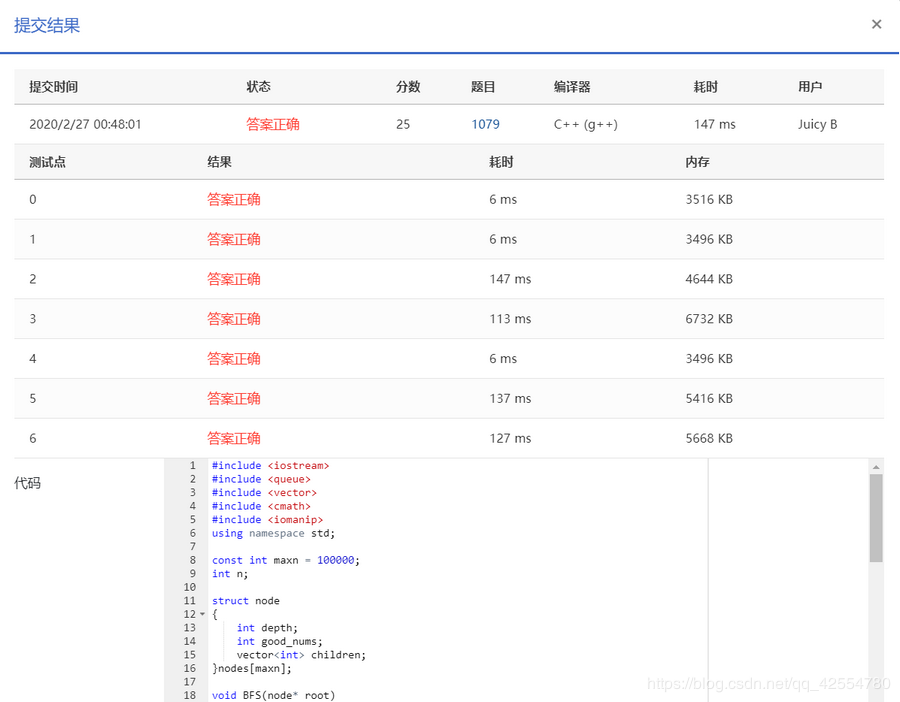
方法一:
方法二:
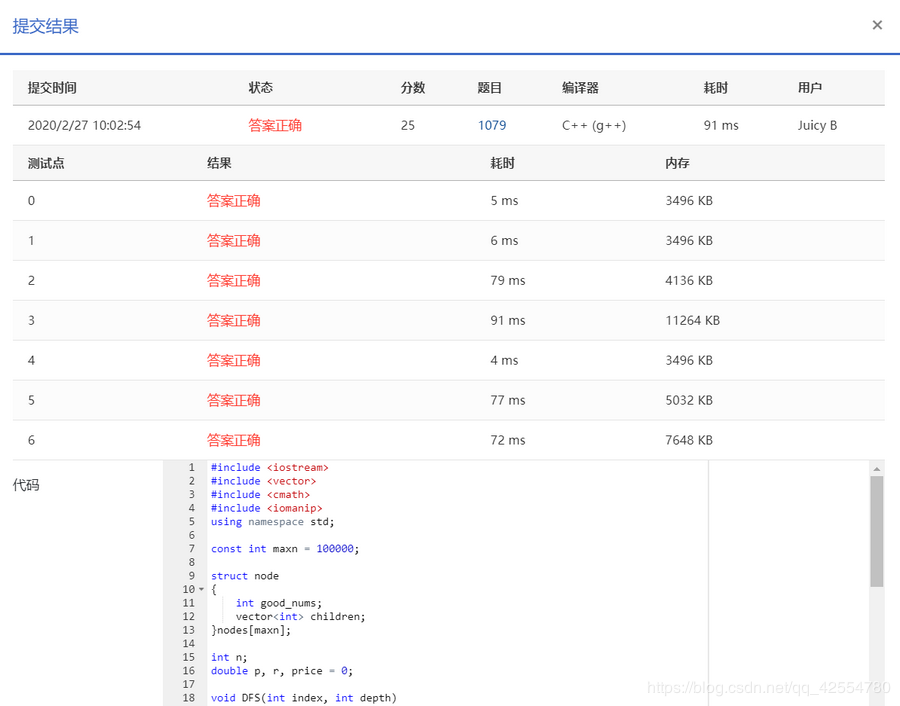
两种方法各有千秋。BFS方法总体上占用内存较小,但耗时较长;DFS方法总体上占用内存较大,但耗时较短。
作者:Juicy B