【MATLAB与机械设计】一维优化之二次插值法(抛物线法)
二次插值法又称抛物线法,它是利用函数在极值点附近具有二次函数的性质建立起来的一种多项式逼近方法。利用目标函数在若干点的信息(函数值、导数值等),构造一个与目标函数值相接近的插值多项式,用该多项式的最优解作为函数的近似最优解,随着搜索区间的逐次缩短,多项式的最优点与原函数最优点的距离逐渐减小,直至满足精度要求。
1.二次插值的程序框图:
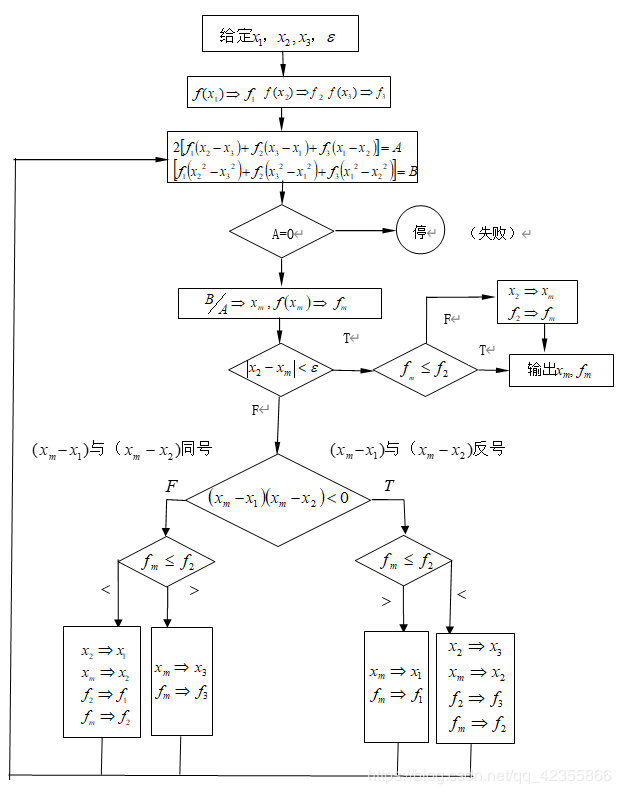
2. MATLAB可执行程序
function [x,f_x]=Quadratic_interpolation(f,x1,x2,x3,exp)
%% 函数说明
%{
本函数应用于二次插值
其中f表示输入函数
x1,x2,x3表示要进行插值的三个点
exp精度
x:为输出的极小值点
f_x:为输出的极小值
调用方法:
clc;
clear;
f=@(x)(x+1/x);
[x,f]=n_d(f,0,10,30,0.01);
x
f
%}
%% 函数主题
f1=f(x1);
f2=f(x2);
f3=f(x3);
%{
sov_f=[f1,f2,f3]';
sov_x=[1,x1,x1^2
1,x2,x2^2
1,x3,x3^2];
sov_a=sov_x\sov_f;
a=sov_a;
a0=a(1);
a1=a(2);
a2=a(3);
%x_m=-a1/(2*a2);
%}
while 1
A=2*(f1*(x2-x3)+f2*(x2-x1)+f3*(x1-x2));
B=(f1*(x2^2-x3^2)+f2*(x2^2-x1^2)+f3*(x1^2-x2^2));
if A==0
disp('run is lost!!')
else
x_m=B/A;
if abs(x2-x_m)<exp
if f(x_m)<=f2
x=x_m;
f_x=f(x_m);
break
else
x=x2;
f_x=f2;
break
end
else
if (x_m-x1)*(x_m-x2)<0
if f(x_m)<=f2
x3=x2;
x2=x_m;
f3=f2;
f2=f(x_m);
else
x1=x_m;
f1=f(x_m);
end
else
if f(x_m)<=f2
x1=x2;
x2=x_m;
f1=f2;
f2=f(x_m);
else
x3=x_m;
f3=f(x_m);
end
end
end
end
end
end
作者:Mach_Pupil