C语言实现各种排序算法实例代码(选择,冒泡,插入,归并,希尔,快排,堆排序,计数)

Kathy ·

更新时间:2024-11-10

· 1437 次阅读

前言

选择排序

冒泡排序

插入排序

归并排序

希尔排序

快速排序

堆排序

计数排序

总结

前言

平时用惯了高级语言高级工具高级算法，难免对一些基础算法感到生疏。但最基础的排序算法中实则蕴含着相当丰富的优化思维，熟练运用可起到举一反三之功效。

选择排序

选择排序几乎是最无脑的一种排序算法，通过遍历一次数组，选出其中最大（小）的值放在新数组的第一位；再从数组中剩下的数里选出最大（小）的，放到第二位，依次类推。

算法步骤

设数组有n个元素，{ a 0 , a 1 , … , a n }

从数组第i ii位开始便利，找到最大值，将之与数组第i ii位交换位置。

i ii从0循环到n。

由于每次遍历需要计算O ( n ) 次，且需要便利n 次，故时间复杂度为O ( n 2 ) )；由于只在交换的过程中需要额外的数据，所以空间复杂度为O ( n ) 。

C语言实现


//sort.c
void SelectionSort(double *p, int n);
int main(){
    double test[5] = {3,2,5,7,9};
    SelectionSort(test,5);
    for (int i = 0; i < 5; i++)
        printf("%f\n", test[i]);
    return 0;
}
//交换数组中i,j处的值
void mySwap(double *arr, int i, int j){
    double temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
//选择排序
void SelectionSort(double *arr, int n){
    int pMax;
    double temp;
    for (int i = 0; i < n-1; i++){
        pMax = i;
        for (int j = i+1; j < n; j++)
            if (arr[j]>arr[pMax])
                pMax = j;
        mySwap(arr,pMax,i);
    }
}

验证

>gcc sort.c
>a
9.000000
7.000000
5.000000
3.000000
2.000000

冒泡排序

冒泡排序也是一种无脑的排序方法，通过重复走访要排序的数组，比较相邻的两个元素，如果顺序不符合要求则交换两个数的位置，直到不需要交换为止。

算法步骤

设数组有n个元素，{ a 0 , a 1 , … , a n }

比较相邻的元素a i , a i + 1 ,如果a i > a i + 1 ，则交换二者。

由于每遍历一次都可以将最大的元素排到最后面，所以下一次可以少便利一个元素。

重复遍历数组n次

由于每次遍历需要计算O ( n ) 次，且需要遍历n次，故时间复杂度为O ( n 2 ) ，空间复杂度为O ( n ) 。

C语言实现


//冒泡排序
void BubbleSort(double *arr, int n)
{
    n = n-1;
    double temp;
    for (int i = 0; i < n; i++)
    for (int j = 0; j < n-i; j++)
        if (arr[j]>arr[j+1])
            mySwap(arr,i,j);        /*前文定义的函数*/
}

插入排序

插入排序是算法导论中的第一个算法，说明已经不那么无脑了。其基本思路是将数组划分位前后两个部分，前面是有序数组，后面是无序数组。逐个扫描无序数组，将每次扫描的数插入到有序数组中。这样有序数组会越来越长，无序数组越来越短，直到整个数组都是有序的。

算法步骤

设数组有n个元素，{ a 0 , a 1 , … , a n }

假设数组中的第0个数已经有序

取出无序数组的第0个元素，将其与有序数组比较，插入到有序数组中。

可见，插入排序的每次插入都有O ( n )的复杂度，而需要遍历n nn次，所以时间复杂度仍为O ( n 2 ) 。

C语言实现


//插入排序
void InsertionSort(double *arr, int n){
    double temp;
    int j;
    for (int i = 1; i < n; i++){
        j = i-1;
        temp  = arr[i];
        while (temp<arr[j] && j>=0){
            arr[j+1] = arr[j];      //第j个元素后移
            j--;
        }
        arr[j+1] = temp;
    }
}

归并排序

归并排序是算法导论中介绍分治概念时提到的一种排序算法，其基本思路为将数组拆分成子数组，然后令子数组有序，再令数组之间有序，则可以使整个数组有序。

算法步骤

设数组有n个元素，{ a 0 , a 1 , … , a n }

如果数组元素大于2，则将数组分成左数组和右数组，如果数组等于2，则将数组转成有序数组

对左数组和右数组执行1操作。

合并左数组和右数组。

可以发现，对于长度为n nn的数组，需要log 2 n次的拆分，每个拆分层级都有O ( n ) 的时间复杂度和O ( n ) 的空间复杂度，所以其时间复杂度和空间复杂度分别为O ( n log 2 n ) 和O(n)

C语言实现

首先考虑两个有序数组的合并问题


//sort.c
void myMerge(double *arr, int nL, int nR);
int main(){
    int n = 6;
    double arr[6] = {2,4,5,1,3,7};
    Merge(arr,3,3);
    for (int i = 0; i < n; i++)
        printf("%f\n", arr[i]);
    return 0;
}
//两个有序数组的混合,arr为输入数组
//nL、nR分别为左数组和右数组的长度
void Merge(double *arr, int nL, int nR){
    nL = nL-1;                    //左侧最后一个元素的索引
    int sInsert = 0;               //左侧待插入起始值
    double temp;
    for (int i = 1; i <= nR; i++)
    {
        while (arr[nL+i]>arr[sInsert])
            sInsert++;
        if (sInsert<nL+i){
            temp = arr[nL+i];
            for (int j = nL+i; j > sInsert; j--)
                arr[j]=arr[j-1];
            arr[sInsert] = temp; 
        }
        else
            break;    //如果sInsert==nL+i，说明右侧序列无需插入
    }
}

验证

> gcc sort.c
> a
1.000000
2.000000
3.000000
4.000000
5.000000
7.000000

然后考虑归并排序的递归过程


void MergeSort(double *arr, int n);
void myMerge(double *arr, int nL, int nR);
int main(){
    int n = 6;
    double arr[6] = {5,2,4,7,1,3};
    MergeSort(arr,n);
    for (int i = 0; i < n; i++)
        printf("%f\n", arr[i]);
    return 0;
}
void MergeSort(double *arr, int n){
    if (n>2)
    {
        int nL = n/2;
        int nR = n-nL;
        MergeSort(arr,nL);
        MergeSort(arr+nL,nR);
        Merge(arr,nL,nR);
    }
    else if(n==2)
        Merge(arr,1,1);
    //当n==1时说明数组中只剩下一个元素，所以什么也不用做
}

验证

> gcc sort.c
> a
1.000000
2.000000
3.000000
4.000000
5.000000
7.000000

至此，排序算法终于有一点算法的味道了。

希尔排序

据说是第一个突破O ( n 2 ) 的排序算法，又称为缩小增量排序，本质上也是一种分治方案。

在归并排序中，先将长度为n的数组划分为长度为nL和nR的两个数组，然后继续划分，直到每个数组的长度不大于2，再对每个不大于2的数组进行排序。这样，每个子数组内部有序而整体无序，然后将有序的数组进行回溯重组，直到重新变成长度为n的数组为止。

希尔排序的划分策略则不然，这里在将数组划分为nL和nR之后，对nR和nR进行按位排序，使得nL和nR内部无序，但整体有序。然后再将数组进行细分，当数组长度变成1的时候，内部也就谈不上无序了，而所有长度为1的数组整体有序，也就是说有这些子数组所组成的数组是有序的。

算法步骤

设数组有n nn个元素，{ a 0 , a 1 , … , a n }

如果数组元素大于2，则将数组分成左数组和右数组，并对左数组和右数组的元素进行一对一地排序。

对每一个数组进行细分，然后将每个子数组进行一对一地排序。

C语言实现


//希尔排序
void ShellSort(double *arr, int n){
    double temp;
    int j;
    for (int nSub = n/2; nSub >0; nSub/=2)      //nSub为子数组长度
        for (int i = nSub; i < n; i++)
        {
            temp = arr[i];
            for (j = i-nSub; j >= 0&& temp<arr[j]; j -= nSub)
                arr[j+nSub] = arr[j];
            arr[j+nSub] = temp;
        }
}

快速排序

快速排序的分治策略与希尔排序类似，其核心思想都是从组内无序而组间有序出发，当子数组长度缩减至1的时候，则整个数组便是有序的。

算法步骤

设数组有n nn个元素，{ a 0 , a 1 , … , a n }

在数组中随机选出一个基准a m i d

通过a m i d将数组分成两部分，其中左边小于a m i d ，右边大于a m i d 。

对左右子数组重复1、2操作，直到子数组长度为1。

由于快速排序的过程中有一个随机选择，所以其时间复杂度可能会受到这个随机选择的影响，如果运气不好的话，快速排序可能会变成冒泡排序。当然，一般来说运气不会那么差，快速排序的平均时间复杂度为O ( n log 2 n ) 。

C语言实现


//快速排序
void QuickSort(double *arr, int n){
    double pivot = arr[0];      //选取第0个点为基准
    int i = 1;
    int j = n-1;
    while (i<j){
        if (arr[i]<pivot)
            i++;
        else{
            mySwap(arr,i,j);
            j--;
        }
    }
    if (arr[i]>pivot)
        i--;
    mySwap(arr,i,0);
    if (i>1)
        QuickSort(arr,i);    //对i前的数组进行快排
    i++;
    if (i<n-1)
        QuickSort(arr+i,n-i);//对i+1后的数组进行快排
}

堆排序

堆是算法导论中介绍的第一种数据结构，本质是一种二叉树，最大堆要求子节点的值不大于父节点，最小堆反之。由于堆是一种带有节点的数据结构，所以结构表示更加直观。好在二叉树父子节点的序号之间存在简单的递推关系，所以在C语言中可以用数组表示堆，

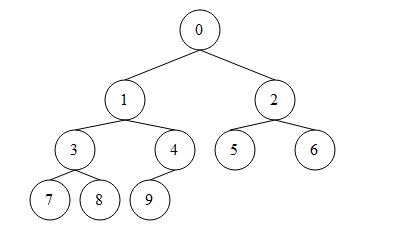
根据上图可知，若父节点的序号为n nn，则左子节点序号为2 n + 1 ,右子节点序号为2 n + 2 。

可以将上图理解为一个排好序的最小堆，如果1位变成15，那么此时这个节点将违反最小堆的原则，经过比对，应该调换15和3的位置。调换之后，15仍然比7和8大，则再调换15和7的位置，则这个最小堆变为

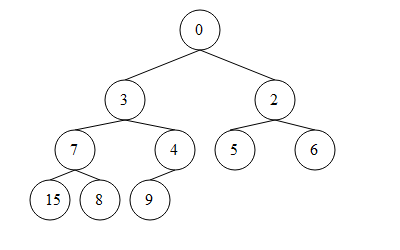
从而继续满足最小堆的性质，最大堆亦然，其C语言实现为


//如果堆中节点号为m的点不满足要求，则调整这个点
//此为最大堆
void adjustHeap(double *arr, int m, int n){
    int left = m*2+1;       //左节点
    while (left<n)
    {
        if (left+1<n)       //判断右节点
            if (arr[left]<arr[left+1])
                left++;     //当右节点大于左节点时，left表示右节点
        if (arr[m]>arr[left])
            break;          //如果父节点大于子节点，则说明复合最大堆
        else{
            mySwap(arr,m,left);
            m = left;
            left = m*2+1;
        }
    }
}

堆的调整过程就是父节点与其左右两个子节点比较的过程，也就是说通过这种方式得到的堆能够满足父子节点的大小关系，但两个孙节点之间并不会被排序。但是，如果一个数组已经满足最大堆要求，那么只需让所有的节点都在根节点处重新参与排序，那么最终得到的最大堆一定满足任意节点间的有序关系。


//堆排序
void HeapSort(double *arr, int n){
    for (int i = n/2; i >= 0; i--)
        adjustHeap(arr,i,n);        //初始化堆
    for (int i = n-1; i > 0 ; i--){
        mySwap(arr,0,i);            //将待排序元素放到最顶端
        adjustHeap(arr,0,i);        //调整最顶端的值 
    }   
}

计数排序

此前所有的排序算法均没有考虑到数组的内在分布，如果我们输入的数据为某个区间内的整数，那么我们只需建立这个区间内的整数索引，然后将每个数归类到这个索引之中即可。

这便是桶排序的思路，所谓桶排序即通过将已知数据划分为有序的几个部分，放入不同的桶中，这个分部过程即桶排序。除了计数排序，基数排序是一种更广泛的桶排序形式，其划分方式可以为数据的位数，把这个桶定义为数据最高位的值。

例如，我们有一组均匀分布在[ 0 , 100 ] 之内的数据，所谓基数排序，即先划分出十个不同的桶[ 0 , 10 ) , [ 10 , 20 ) , … , [ 90 , 100 ) ，然后再对每个桶进行单独的排序。这样划分下去，那么基数排序的复杂度则为O ( 10 ∗ n ) 。

词典中的排序方式也可以理解为一种基数排序，即首先看第一个字母的顺序，然后第二个，依次类推。由于桶排序对数据做了假设，所以其最优时间复杂度可以达到O ( n + k ),k为桶的数目。

例如，我们有一个由一百个由1和2组成的数组，那么我们只需建立一个索引1 : n 1 , 2 : n 2 ，然后统计1和2分别出现的个数即可，其时间复杂度也将变成O ( n ) 。

在这里只做出最简单的计数排序。


/计数排序,输入数组为整数
void CountingSort(int *arr,int n){
    int aMax = arr[0];
    int aMin = arr[0];
    for (int i = 0; i < n; i++) //查找最大值和最小值
        if (arr[i]>aMax)
            aMax = arr[i];
        else if (arr[i]<aMin)
            aMin = arr[i];
    int m = aMax-aMin+1;         //索引长度
    int *arrSort = (int*)malloc(sizeof(int)*m);
    for (int i = 0; i < m; i++)
        arrSort[i]=0;           //初始化索引
    for (int i = 0; i < n; i++) //排序
        arrSort[arr[i]-aMin] += 1;
    n = 0;
    for (int i = 0; i < m; i++)
    {
        aMax = i+aMin;          //此值为真实数据
        for (int j = n; j < n+arrSort[i]; j++)
            arrSort[j] = i+aMin;
        n += arrSort[i];
    }
}

总结

到此这篇关于C语言实现各种排序算法(选择,冒泡,插入,归并,希尔,快排,堆排序,计数)的文章就介绍到这了,更多相关C语言实现各种排序算法内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网！

选择快排排序算法 C语言堆排序算法排序