Python:花了好久才写完的拉格朗日差值法和牛顿差商法的实现
Python:花了好久才写完的拉格朗日差值法和牛顿差商法的实现
首先拉格朗日差值公式如下:
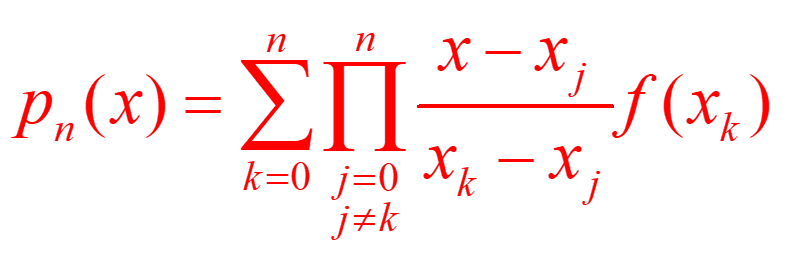
那么这个公式的思想是什么呢?
1.得到的差值计算式必须穿过所有的已知的节点。(已知节点必须互异:即已知点不重合)
2.当x=xi,对应的某一项系数必须为1,而其他项的系数均为0,此时结果为yi。
3.通过1和2的思想去构造系数因子,可以得到如下结果:
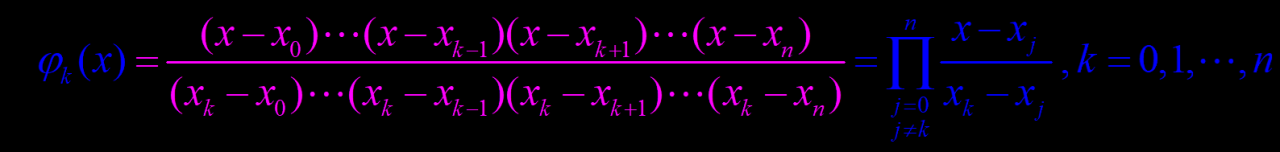
4.将得到的xi…xn与对应的yi…yn相乘得到最终的拉格朗日差值公式。
算法实现的角度考虑,如何对系数因子的变化规律进行变化式的实现呢?
1.假设有n个已知节点,那么则需产生n个拉格朗日系数因子。这里我们首先想到的是遍历令k=0,到n-1。
2.关于k与j之间的要求是:k!=j,且j从0遍历到n-1,当j==n-1时,第k项的系数因子时将不再变化。
那么我们来结合代码,看一看:
def coefficient(vari, k, i, n):#vari代表输入的变量,k代表这是第k项的系数因子式,i相当于j,初始值为0,n即为n项节点。
if i >= n - 1:
if i > n-1:
return 1
elif k != n-1:
return (vari - x[n-1]) / (x[k] - x[n-1])
else:
return 1
elif i != k:
return (vari - x[i]) / (x[k] - x[i]) * coefficient(vari, k, i+1, n)
else:
return (vari - x[i+1]) / (x[k] - x[i+1]) * coefficient(vari, k, i+2, n)
这里的设计思想有几点需要说明:
当i>=n-1时,即发生越界返回1,完成递归计算。而不是i=n,因为注意最后一行代码的coefficient(vari, k, i+2, n),这个地方i+2,假设i=k,而此时的k=n-1,那么经过i+2,i变成n+1,越界条件不成立了。
而对i>=n-1的情况还要细分:i>n-1越界,返回1,完成递归;i=n-1,但是k!=n-1意味着正常结束,返回系数因子式 (vari - x[n-1]) / (x[k] - x[n-1])。重点来了,这里有个特别特别的细节!!!如果k=n-1,那么最后一项返回的不是(vari - x[n-1]) / (x[k] - x[n-1]),而是1。(仔细体会这一点!!!)
而当i<n-1时,当i!=k时,采用递归做法i=i+1;则选择跳过,i=i+2。
最后加上主程序的代码其他部分:
a = input("请输入若干个互异的节点的x轴坐标值:")
x = [float(i) for i in a.split(" ")]
b = input("请输入若干个互异的节点的y轴坐标值:")
y = [float(j) for j in b.split(" ")]
n = len(x)
sum = 0
v = float(input("请输入需要计算的节点的x轴坐标值:"))
for k in range(n):
increase = (y[k]) * coefficient(v, k, 0, n)
print("系数为:"+str(increase))
sum += increase
print("x=%f, y=%f" % (v, sum))
测试的样例:
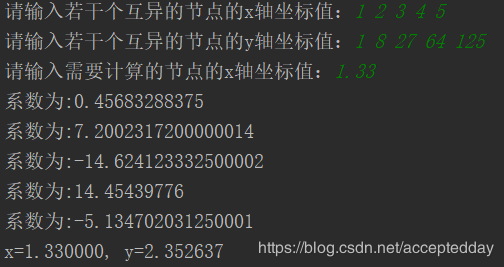
关于差商表的构造和理解,可以参考这篇博客的讲解:
https://blog.csdn.net/deramer1/article/details/79037740
然后我们给出差商表的结构如下:(这张表非常重要,后面的算法实现全部基于这张表!)
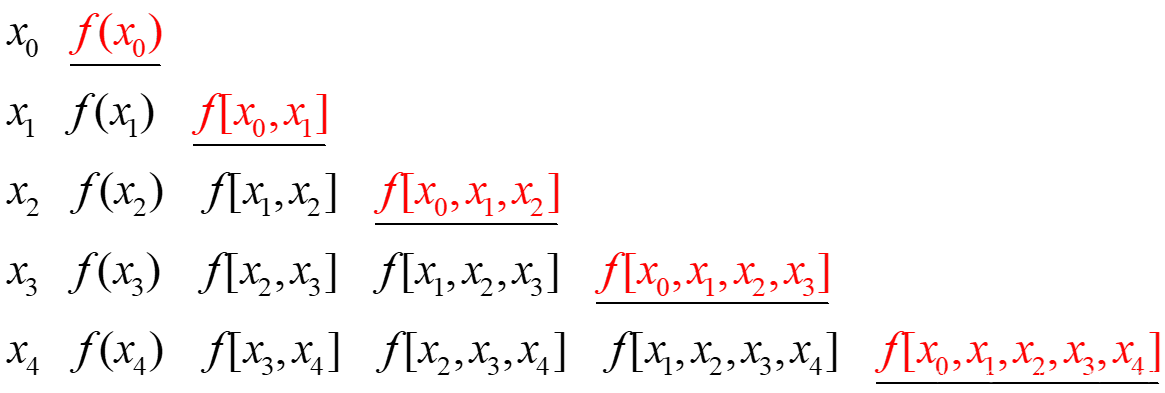
![]()

然后给出基于牛顿差商表的牛顿差值公式:
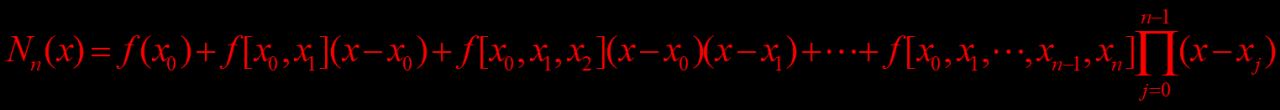
最后我们来到了牛顿插值法最关键的算法实现部分,整个设计的思路是这样的:
1.初始化差商表,将xixn和yiyn填入表格完成n*n的表格的初始化。
initial = [] # 初始化表格Table
for p in range(n+1):
initial.append([])
for q in range(n):
initial[p].append(None) # 生成n*n的二维列表,同时列表元素初始化为0
for k in range(n):
initial[0][k] = x[k]
initial[1][k] = y[k]
print("初始化后的表格如下:")
print(initial) # 将x和y的值填入表格,完成Table的初始化。
2.根据表格位置之间的数据关系,基于这种关系进行填表。(这也是最核心的部分)
def Qda_Table():
for i in range(n+1):#i代表列,j代表行
for j in range(n):
if initial[i][j] is not None or i >= j + 2:
continue
else:
initial[i][j] = (initial[i - 1][j] - initial[i - 1][j - 1]) / (
initial[0][j] - initial[0][j - i + 1])
# print("%d,%d的当前值为:" % (i, j) + str(initial[i][j]))
这里需要注意的是:
在当前的位置处于"上三角"的部分或not None的部分,直接跳过。要结合差商表看。
而当处于需要填充的位置时,这里的方式是依次遍历当前这一列的每一行去填充数据,基于位置关系。
3.变量因子式也要采用递归去完成,用一个自定义递归函数实现。
def calculate_factors(no, vari): # 计算每次的相乘的自变量因子多项式
factor = 1
if no == 1:
return factor
else:
for i in range(no-1):
factor = factor *(vari-x[i])
return factor
4.在最后的牛顿差值计算式中查表得到相应的系数乘以相应的变量因子式(像(x-x0)(x-x1)…这种)。
def final_calculate():
result = 0
for time in range(n):
result = result + initial[time+1][time] * calculate_factors(time+1, v)
return result
最后完成主程序的代码部分:
a = input("请输入若干个互异的节点的x轴坐标值:")
x = [float(i) for i in a.split(" ")]
b = input("请输入若干个互异的节点的y轴坐标值:")
y = [float(j) for j in b.split(" ")]
n = len(x)
sum = 0
v = float(input("请输入需要计算的节点的x轴坐标值:"))
Qda_Table() # 计算每个位置的差商填表
QDA_table = np.array(initial).T # 转置后输出结果
print("最终的差商表格如下:")
print(QDA_table)
print("x=%f最终的计算结果为:%f" % (v, final_calculate()))
测试的样例:
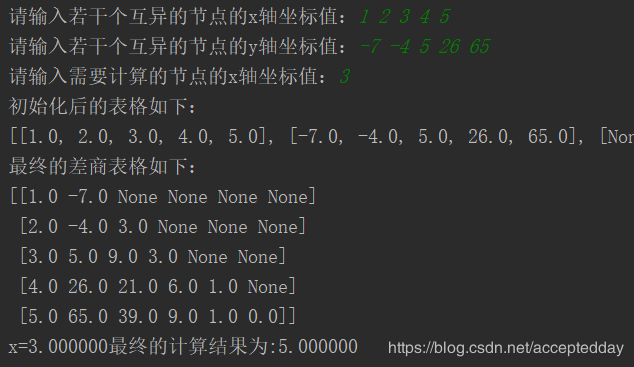
作者:为学习痴狂的大鱼