《Learning to Count Objects in Natural Images for Visual Question Answering》论文笔记

问题的提出在于计数类问题在很多模型上表现性能不佳，作者分析出现这类问题是源于软注意力机制 （Soft-Attention），进而提出了一个计数模块

在 VQA 领域中，造成计数类问题表现不佳的原因主要有：(1) Soft-Attention 的广泛运用，(2) 区别于标准的计数问题，对于 VQA 来说，没有明确的标签标定需要计数对象的位置，(3) VQA 系统的复杂性，表现在不仅要处理计数类问题，同时还要兼顾其他复杂的问题，(4) 真实场景中，对某个对象区域可能存在多次重叠采样。

截至目前，即使是 Hard Attention 和 structured Attention 表现也并不乐观（所列举的论文采用限制 Attention 每次作用域单个 Bounding box），直观的解释比如一张图片有两只猫，各自分得了 0.5 的权重，在做信息加权时候，则又退化到一只猫的情况。另外文章还表示 sigmoid 函数作为激活函数，在处理计数问题时，效果并不好。

本文的关键思想在于将相关 object proposal 描述成点 VVV， 其间的内部与外部关系描述成边 EEE，形成图 G=(V,E)G = (V, E)G=(V,E)，全文设计策略，通过在极端情况分析，设计算法，而实际的激活函数学习到的参数可适用于真实场景

前面提到过 Sigmoid 函数不适合用作激活函数，所以本文提出了分段线性激活函数 f1,...,f8f_1,...,f_8f1​,...,f8​ 替代 sigmoid 函数。约束条件：(1) fk(0)=1,fk(1)=1f_k(0)=1,f_k(1)=1fk​(0)=1,fk​(1)=1，(2) 单调递增，用来逼近区间[0,1][0,1][0,1]任意的函数。具体来说，将[0,1][0,1][0,1] 等分成 ddd 个区间，每个小区间包含一个线性片段来连接周围的区间。对每个函数 fkf_kfk​，有 ddd 个权重参数 wk1,...,wkdw_{k1},..., w_{kd}wk1​,...,wkd​分别隶属于区间[i−1d,id)[\frac{i-1}{d},\frac{i}{d})[di−1​,di​)，整个函数可以写成：
fk(x)=∑i=1dmax(0,1−∣dx−i∣)∑j=1i∣wkj∣∑m=1d∣wkm∣          (1) f_k(x)=\sum_{i=1}^dmax(0,1-|dx-i|)\frac{\sum_{j=1}^i|w_{kj}|}{\sum_{m=1}^d|w_{km}|} \ \ \ \ \ \ \ \ \ \ (1) \\ fk​(x)=i=1∑d​max(0,1−∣dx−i∣)∑m=1d​∣wkm​∣∑j=1i​∣wkj​∣​          (1)
实验表明，d=16d = 16d=16 时效果较好。为后文理解简单起见，可以视为起到了 sigmoid 函数作用。

以图的形式表达，这点类似于 GCN 网络的思想。相关 object proposal 表示成黑点，不相关 object proposal 表示成白点，红色边表示潜在检测目标的内部联系（Intra-），蓝色边表示外部联系（Inter-），如下图所示，注意对橘猫检测出现了两个重复的 proposal（仅做极端示例，实际难以出现这类结果）

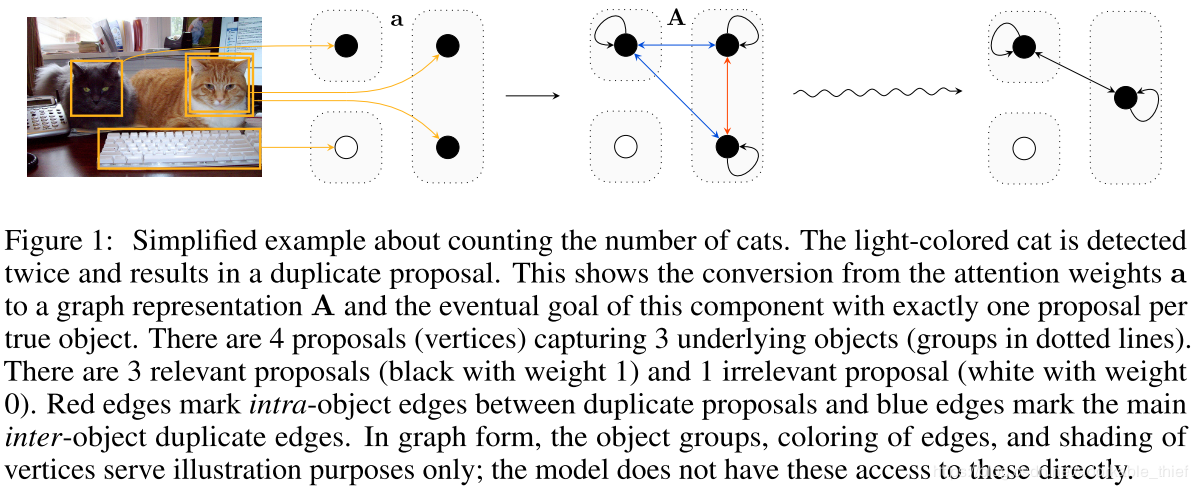
模型的输入包括注意力权重 a=[a1,...,an]Ta = [a_1,...,a_n]^Ta=[a1​,...,an​]T （值限制在[0,1]）和相对应的 bounding boxes b=[b1,...,bn]b = [b_1, ..., b_n]b=[b1​,...,bn​]，考虑极端的情况下，对第 iii 个相关 proposal 注意力权重赋值 1，不相关则赋值 0，将注意力权重信息转化为有向图的表达型式：A=aaTA = aa^TA=aaT，由图的性质可知，∣E∣=∣V∣2|E|=|V|^2∣E∣=∣V∣2（带自环），且 ∣E∣=∑iai\sqrt{|E|}= \sum_ia_i∣E∣​=∑i​ai​，其中顶点 VVV 表示相关 proposal，EEE 表示顶点 (i,j)(i,j)(i,j) 间的权重乘积 aiaja_ia_jai​aj​

模型可能会出现对潜在目标对象的重复采样，如图 1 中的橘猫，所以需要想办法消除重复采样中的 Intra- 关联。在有向图中，通过类似于 Mask 的操作（这里的 Mask 矩阵就是距离矩阵 DDD），DDD 描述了两个采样框的重叠程度，其中 IOU 是交并比计算公式：
Dij=1−IOU(bi,bj)          (2) D_{ij}=1-IOU(b_i,b_j) \ \ \ \ \ \ \ \ \ \ (2) \\ Dij​=1−IOU(bi​,bj​)          (2)
通过 element-wise product 做 Mask，就可以消除 Intra-object edges：
A~=f1(A)⊙f2(D)          (3) \tilde{A} = f_1(A) \odot f_2(D) \ \ \ \ \ \ \ \ \ \ (3) \\ A~=f1​(A)⊙f2​(D)          (3)
注意经过处理的图缺少了自环，要重新加上去。文章并没有说明具体怎么做，所以我认为可行的方法有将 DDD 的对角线元素值置为 1

A′~\tilde{A{'}}A′~ 是对 A~\tilde{A}A~ 加入自环后的图，去除 Inter-object 边的方法是通过缩减相关边的权重：考虑下图检测橘猫抽象出的两个黑点（对同一个目标对象的两次采样），它们指向同一个目标对象（左上角的黑点）的边有两条，因此将这两条边的权值乘以 0.5，在最初描述 Attention 机制不适用于计数问题时说过，由于最后的加权平均，这就相当于将两个黑点归为一个。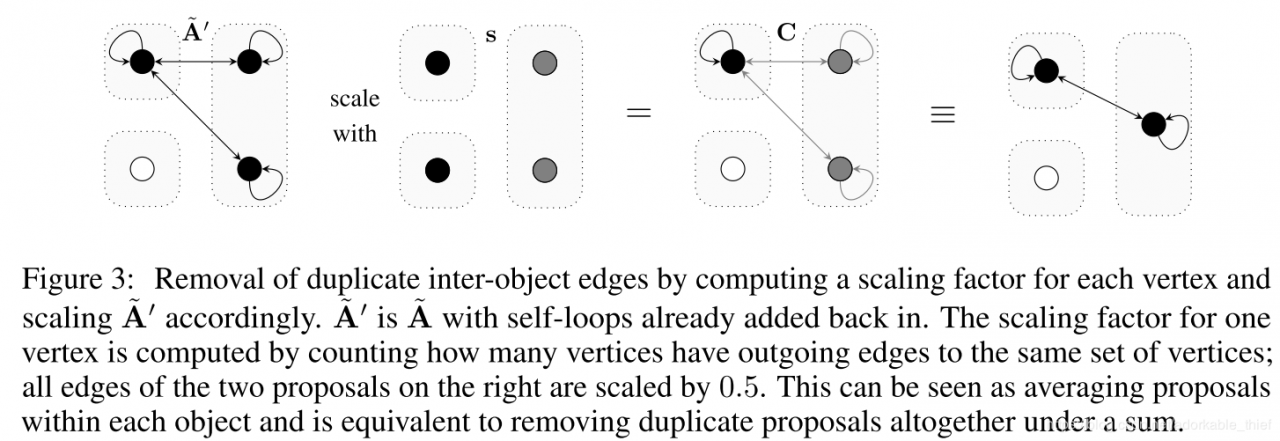

要完成上面的流程，就需要判断哪些采样属于同一个目标对象。极端情况下，对于同一个目标对象的两次采样，在邻接矩阵上反映出来的是两行的值一一相同；反之如果有一处不同，则可断定两个采样不属于同一个目标对象。因此可以定义顶点 i,ji,ji,j 相似度 SimijSim_{ij}Simij​ 来描述二者否属于同一个目标对象：
Simij=f3(1−∣ai−aj∣)∏kf3(1−∣Xik−Xjk∣)          (4) Sim_{ij}=f_3(1-|a_i-a_j|)\prod_kf_3(1-|X_{ik}-X_{jk}|) \ \ \ \ \ \ \ \ \ \ (4) \\ Simij​=f3​(1−∣ai​−aj​∣)k∏​f3​(1−∣Xik​−Xjk​∣)          (4)
其中 X=f4(A)⊙f5(D)X = f_4(A) \odot f_5(D)X=f4​(A)⊙f5​(D)，XXX 不包含自环。当只有一个 proposal 计数时（记为 iii），如果不加第一项就会导致在 ai=1a_i=1ai​=1 情况下错误计算 aj≠i=0a_{j \ne i } = 0aj​=i​=0 的相似度。

对每一个顶点通过相似度计算，进一步的可以得到第 iii 个 proposal 缩放因子：
si=1/∑jSimij          (5) s_i = 1/\sum_jSim_{ij} \ \ \ \ \ \ \ \ \ \ (5) \\ si​=1/j∑​Simij​          (5)
将缩放因子扩展成矩阵形式方便与邻接矩阵做运算，注意第一项所得到的图没有自环，所以第二项加上自环：
C=A~⊙ssT+diag(s⊙f1(a⊙a))          (6) C = \tilde{A} \odot ss^T + diag(s \odot f_1(a \odot a)) \ \ \ \ \ \ \ \ \ \ (6)\\ C=A~⊙ssT+diag(s⊙f1​(a⊙a))          (6)
注意这里有一个细节：第二项同样可以用 diag(s⊙s)diag(s \odot s)diag(s⊙s) 计算，但这样做由于非对角线元素相当于做了平方级的运算，但对角线元素仅仅做了一个线性的缩放。

通过上述的计算过程得到的 CCC 表示了一个连接相关对象，包含自环的图（如图 3）所示。从 CCC 上计数相关目标，令 ∣E∣=∑i,jCi,j|E|=\sum_{i,j}C_{i,j}∣E∣=∑i,j​Ci,j​，则有 c=∣V∣=∣E∣c=|V|=\sqrt{|E|}c=∣V∣=∣E∣​，最后将 ccc 转换成 one-hot 向量型式 o=[o1,o2,...,on]To=[o_1,o_2,...,o_n]^To=[o1​,o2​,...,on​]T
oi=max(0,1−∣c−i∣)          (7) o_i=max(0,1-|c-i|) \ \ \ \ \ \ \ \ \ \ (7) oi​=max(0,1−∣c−i∣)          (7)
考虑到如果 aaa 和 DDD 的值更接近于 0 或者 1 时更可信。因此对数据做了类似于平移操作：
pa=1n∑i∣f6(ai)−0.5∣          (8)pD=1n2∑i,j∣f7(Dij)−0.5∣          (9) p_a=\frac{1}{n}\sum_i |f_6(a_i)-0.5| \ \ \ \ \ \ \ \ \ \ (8) \\p_D=\frac{1}{n^2}\sum_{i,j}|f_7(D_{ij})-0.5| \ \ \ \ \ \ \ \ \ \ (9) \\ pa​=n1​i∑​∣f6​(ai​)−0.5∣          (8)pD​=n21​i,j∑​∣f7​(Dij​)−0.5∣          (9)
这里假定了均值为 0.5，不过这个不影响，因为 fkf_kfk​ 的学习机制可以做有效的调整。最后定义输出：
o~=f8(pa+pD)⋅o          (10) \tilde{o}=f_8(p_a+p_D) \cdot o \ \ \ \ \ \ \ \ \ \ (10) \\ o~=f8​(pa​+pD​)⋅o          (10)

⋄\diamond⋄ 表示特征融合，简单地以 x⋄y=ReLU(Wxx+Wyy)−(Wxx−Wyy)2x \diamond y=ReLU(W_xx+W_yy)-(W_xx-W_yy)^2x⋄y=ReLU(Wx​x+Wy​y)−(Wx​x−Wy​y)2 作为融合策略的基准（第一项简单地使用 ReLU 做融合，第二项用于测量经过映射后的 x,yx, yx,y 的距离），模型架构如下所示，具体实验参数可以参照原论文。

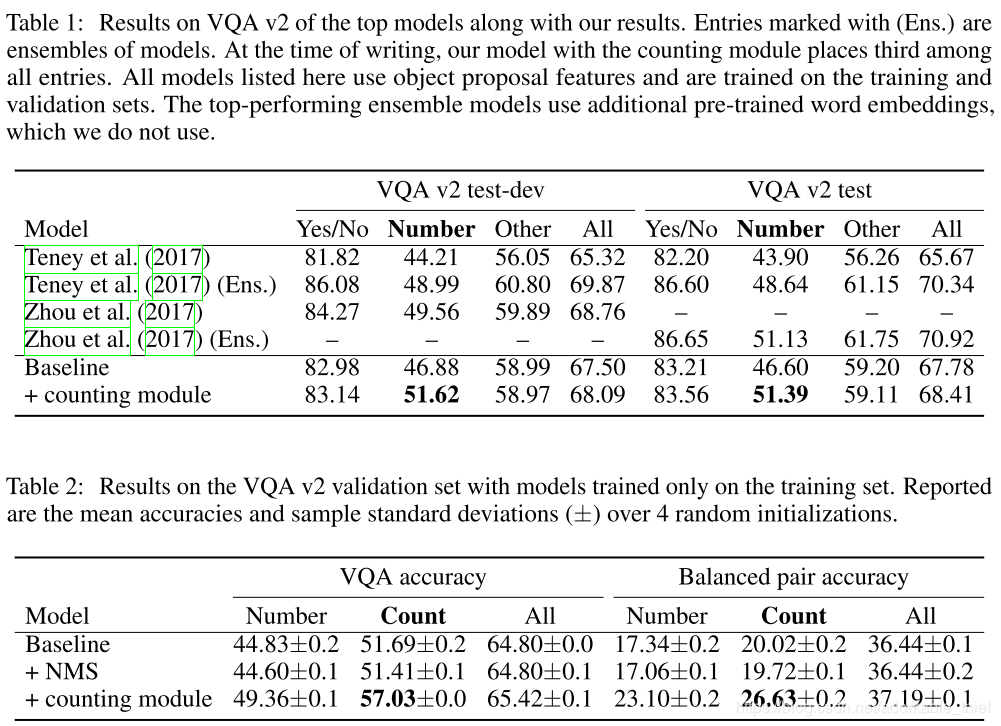
VQA 实验结果如下所示，表一二的结果表明在加入计数模块在处理计数类问题时，达到了 state-of-the-art

《LEARNING TO COUNT OBJECTS IN NATURAL IMAGES FOR VISUAL QUESTION ANSWERING》

count NATURAL TO for visual