3.11 模型选择、欠拟合和过拟合
讨论了:当模型在训练数据集上更准确时,它在测试数据集上却不一定更准确的原因。
3.11.1 训练误差和泛化误差训练误差(training error):模型在训练数据集上表现出的误差。
泛化误差(generalization error):模型在任意一个测试数据样本上表现出的误差的期望,并常常通过测试数据集上的误差来近似。
在机器学习里,我们通常假设训练数据集(训练题)和测试数据集(测试题)里的每一个样本都是从同一个概率分布中相互独立地生成的。
机器学习模型应关注降低泛化误差。
3.11.2 模型选择在机器学习中,通常需要评估若干候选模型的表现并从中选择模型。这一过程称为模型选择(model selection)。
验证数据集
预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集,简称验证集(validation set)。
KKK 折交叉验证
在KKK折交叉验证中,我们把原始训练数据集分割成KKK个不重合的子数据集,然后我们做KKK次模型训练和验证。每一次,我们使用一个子数据集验证模型,并使用其他K−1K-1K−1个子数据集来训练模型。在这KKK次训练和验证中,每次用来验证模型的子数据集都不同。最后,我们对这KKK次训练误差和验证误差分别求平均。
3.11.3 欠拟合和过拟合欠拟合(underfitting):一模型无法得到较低的训练误差。
过拟合(overfitting):模型的训练误差远小于它在测试数据集上的误差
导致的两个因素:模型复杂度和训练数据集大小。
模型复杂度
以多项式函数拟合为例,给定一个由标量数据特征xxx和对应的标量标签yyy组成的训练数据集,多项式函数拟合的目标是找一个KKK阶多项式函数
y^=b+∑k=1Kxkwk\hat{y} = b + \sum_{k=1}^K x^k w_ky^=b+k=1∑Kxkwk
来近似yyy。
在上式中,wkw_kwk是模型的权重参数,bbb是偏差参数。与线性回归相同,多项式函数拟合也使用平方损失函数。特别地,一阶多项式函数拟合又叫线性函数拟合。
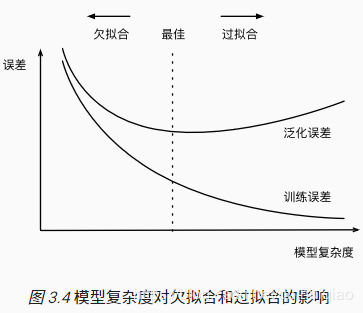
因为高阶多项式函数模型参数更多,模型函数的选择空间更大,所以高阶多项式函数比低阶多项式函数的复杂度更高。因此,高阶多项式函数比低阶多项式函数更容易在相同的训练数据集上得到更低的训练误差。给定训练数据集,模型复杂度和误差之间的关系通常如图3.4所示。给定训练数据集,如果模型的复杂度过低,很容易出现欠拟合;如果模型复杂度过高,很容易出现过拟合。应对欠拟合和过拟合的一个办法是针对数据集选择合适复杂度的模型。
训练数据集大小
一般来说,如果训练数据集中样本数过少,特别是比模型参数数量(按元素计)更少时,过拟合更容易发生。此外,泛化误差不会随训练数据集里样本数量增加而增大。因此,在计算资源允许的范围之内,我们通常希望训练数据集大一些,特别是在模型复杂度较高时,例如层数较多的深度学习模型。
3.11.4 多项式函数拟合实验为了理解模型复杂度和训练数据集大小对欠拟合和过拟合的影响,下面我们以多项式函数拟合为例来实验。
Mxnet:
%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, nd
from mxnet.gluon import data as gdata, loss as gloss, nn
Pytorch:
%matplotlib inline
import torch
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
生成数据集
生成人工数据集。使用如下的三阶多项式函数来生成该样本的标签:
y=1.2x−3.4x2+5.6x3+5+ϵ,y = 1.2x - 3.4x^2 + 5.6x^3 + 5 + \epsilon,y=1.2x−3.4x2+5.6x3+5+ϵ,
其中噪声项ϵ\epsilonϵ服从均值为0、标准差为0.1的正态分布。训练集和测试集的样本数都设为100。
Mxnet:
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = nd.random.normal(shape=(n_train + n_test, 1))
poly_features = nd.concat(features, nd.power(features, 2),
nd.power(features, 3))
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
+ true_w[2] * poly_features[:, 2] + true_b)
labels += nd.random.normal(scale=0.1, shape=labels.shape)
Pytorch:
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = torch.randn((n_train + n_test, 1))
poly_features = torch.cat((features, torch.pow(features, 2), torch.pow(features, 3)), 1)
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
+ true_w[2] * poly_features[:, 2] + true_b)
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
定义、训练和测试模型
我们先定义作图函数semilogy,其中yyy轴使用了对数尺度。
# 本函数已保存在d2lzh包中方便以后使用
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None, figsize=(3.5, 2.5)):
d2l.set_figsize(figsize)
d2l.plt.xlabel(x_label)
d2l.plt.ylabel(y_label)
d2l.plt.semilogy(x_vals, y_vals)
if x2_vals and y2_vals:
d2l.plt.semilogy(x2_vals, y2_vals, linestyle=':')
d2l.plt.legend(legend)
和线性回归一样,多项式函数拟合也使用平方损失函数。因为我们将尝试使用不同复杂度的模型来拟合生成的数据集,所以我们把模型定义部分放在fit_and_plot函数中。
Mxnet:
num_epochs, loss = 100, gloss.L2Loss()
def fit_and_plot(train_features, test_features, train_labels, test_labels):
net = nn.Sequential()
net.add(nn.Dense(1))
net.initialize()
batch_size = min(10, train_labels.shape[0])
train_iter = gdata.DataLoader(gdata.ArrayDataset(
train_features, train_labels), batch_size, shuffle=True)
trainer = gluon.Trainer(net.collect_params(), 'sgd',
{'learning_rate': 0.01})
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
train_ls.append(loss(net(train_features),
train_labels).mean().asscalar())
test_ls.append(loss(net(test_features),
test_labels).mean().asscalar())
print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('weight:', net[0].weight.data().asnumpy(),
'\nbias:', net[0].bias.data().asnumpy())
Pytorch:
num_epochs, loss = 100, torch.nn.MSELoss()
def fit_and_plot(train_features, test_features, train_labels, test_labels):
net = torch.nn.Linear(train_features.shape[-1], 1)
# 通过Linear文档可知,pytorch已经将参数初始化了,所以我们这里就不手动初始化了
batch_size = min(10, train_labels.shape[0])
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y.view(-1, 1))
optimizer.zero_grad()
l.backward()
optimizer.step()
train_labels = train_labels.view(-1, 1)
test_labels = test_labels.view(-1, 1)
train_ls.append(loss(net(train_features), train_labels).item())
test_ls.append(loss(net(test_features), test_labels).item())
print('final epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('weight:', net.weight.data,
'\nbias:', net.bias.data)
三阶多项式函数拟合(正常)
使用三阶多项式函数拟合。实验表明,这个模型的训练误差和在测试数据集的误差都较低。训练出的模型参数也接近真实值:w1=1.2,w2=−3.4,w3=5.6,b=5w_1 = 1.2, w_2=-3.4, w_3=5.6, b = 5w1=1.2,w2=−3.4,w3=5.6,b=5。
fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:])
线性函数拟合(欠拟合)
使用线性函数拟合。很明显,该模型的训练误差在迭代早期下降后便很难继续降低。在完成最后一次迭代周期后,训练误差依旧很高。
fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],
labels[n_train:])
训练样本不足(过拟合)
只使用两个样本来训练模型。显然,训练样本过少了,甚至少于模型参数的数量。这使模型显得过于复杂,以至于容易被训练数据中的噪声影响。在迭代过程中,尽管训练误差较低,但是测试数据集上的误差却很高。这是典型的过拟合现象。
fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],
labels[n_train:])
我们将在接下来的两个小节继续讨论过拟合问题以及应对过拟合的方法。
小结 由于无法从训练误差估计泛化误差,一味地降低训练误差并不意味着泛化误差一定会降低。机器学习模型应关注降低泛化误差。 可以使用验证数据集来进行模型选择。 欠拟合指模型无法得到较低的训练误差,过拟合指模型的训练误差远小于它在测试数据集上的误差。 应选择复杂度合适的模型并避免使用过少的训练样本。作者:咕噜呱啦