ESL2.9 模型选择和偏差-方差的权衡学习笔记
这是一篇有关《统计学习基础》,原书名The Elements of Statistical Learning的学习笔记,该书学习难度较高,有很棒的学者将其翻译成中文并放在自己的个人网站上,翻译质量非常高,本博客中有关翻译的内容都是出自该学者的网页,个人解读部分才是自己经过查阅资料和其他学者的学习笔记,结合个人理解总结成的原创内容。
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 时间 | 2018-08-21 |
| 解读 | Hytn Chen |
| 更新 | 2020-02-12 |
上面讨论的所有模型以及其他将要在后面章节讨论的模型都有一个 光滑 (smoothing) 或 复杂性 (complexity) 参数需要确定:
惩罚项的乘子 核的宽度 基函数的个数在光滑样条的情形下,参数 λ\lambdaλ 表示了从直线拟合到插值的各种模型.类似地,degree 为 mmm 的局部多项式模型从 窗宽 (window size) 无限大时阶为 mmm 的全局多项式到 窗宽 (window size) 至零时的插值拟合模型.这意味着我们不能用训练数据的残差平方和来确定这些参数,因为我们总是选择插值拟合,因为能达到零残差.这样的一个模型不可能用来预测未来的数据.
kkk 最近邻回归的拟合值 f^k(x0)\hat{f}_k(x_0)f^k(x0) 有效地说明了其有与上述近似方法的竞争力.假设数据来自模型 Y=f(X)+ϵ,E(ϵ)=0,Var(ϵ)=σ2Y=f(X)+\epsilon, \rm{E}(\epsilon)=0,\rm{Var}(\epsilon)=\sigma^2Y=f(X)+ϵ,E(ϵ)=0,Var(ϵ)=σ2.为了简化,我们假设样本中的值 xix_ixi 提前修正好(不是随机).在 x0x_0x0 处的期望预测误差,也被称为 测试 (test) 或 泛化 (generalization) 误差,可按如下方式分解:
EPEk(x0)=E[(Y−f^k(x0))2∣X=x0]=σ2+[Bias2(f^k(x0))+VarT(f^k(x0))]=σ2+[f(x0)−1k∑ℓ=1kf(x(ℓ))]2+σ2k
\begin{aligned}
\rm{EPE}_k(x_0)&=\rm{E}[(Y-\hat{f}_k(x_0))^2\mid X=x_0]\\
&=\sigma^2+[Bias^2(\hat{f}_k(x_0))+Var_{\mathcal T}(\hat{f}_k(x_0))]\\
&=\sigma^2+[f(x_0)-\frac{1}{k}\sum\limits_{\ell=1}^kf(x_{(\ell)})]^2+\frac{\sigma^2}{k}
\end{aligned}
EPEk(x0)=E[(Y−f^k(x0))2∣X=x0]=σ2+[Bias2(f^k(x0))+VarT(f^k(x0))]=σ2+[f(x0)−k1ℓ=1∑kf(x(ℓ))]2+kσ2
带括号的下标 (ℓ)(\ell)(ℓ) 表示 x0x_0x0 的最近邻的顺序.
在展开式中有三项.第一项 σ2\sigma^2σ2 是 不可约减的 (irreducible) 误差——是新测试目标点的方差——而且我们不能够控制,即使我们知道真值 f(x0)f(x_0)f(x0)
第二项和第三项在我们的控制范围内,并且构成了估计 f(x0)f(x_0)f(x0) 时 f^k(x0)\hat f_k(x_0)f^k(x0) 的 均方误差 (mean squared error),均方误差经常被分解成偏差部分和方差部分.偏差项是真值均值 f(x0)f(x_0)f(x0) 与估计的期望值之间差异的平方——[ET(f^_k(x0))−f(x0)]2[\rm{E}_{\mathcal T}(\hat{f}\_k(x_0))-f(x_0)]^2[ET(f^_k(x0))−f(x0)]2——其中期望平均了训练数据中的随机量.如果真实的函数相当地光滑,这一项很可能随着 kkk 的增加而增加.对于较小的 kkk 值和较少的近邻点会导致值 f(x(ℓ))f(x_{(\ell)})f(x(ℓ)) 与 f(x0)f(x_0)f(x0) 很接近,所以它们的平均应该距离 f(x0)f(x_0)f(x0) 很近.当 kkk 值增加,邻域远离,然后任何事情都可能发生.
这里的方差项是方差的简单平均,因为 kkk 的倒数关系,随 kkk 变大而变小.所以当 kkk 变化,会有 偏差——误差的权衡 (bias-variance tradeoff).
更一般地,随着我们过程的 模型复杂度 (model complexity) 增加,方差趋于上升,偏差趋于下降.当模型复杂度下降时会发生相反的行为.对于 kkk-最近邻,模型复杂度由 kkk 来控制.
一般地,我们选择模型复杂度使偏差与方差达到均衡从而使测试误差最小.测试误差的一个明显的估计是 训练误差 (training error) 1N∑i(yi−y^i)2\frac{1}{N}\sum_i(y_i-\hat{y}_i)^2N1∑i(yi−y^i)2.不幸的是,训练误差不是测试误差的良好估计,因为这不能解释模型复杂度.
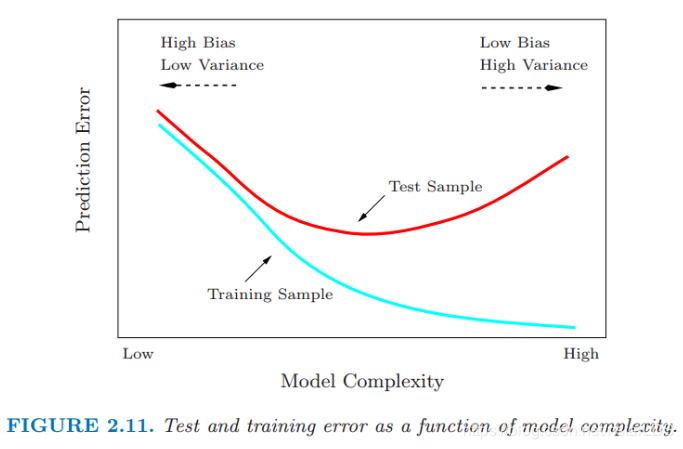
图2.11:测试和训练错误随模型复杂度变化
图 2.11 显示了不同模型复杂度下测试和训练误差的一般表现.无论何时增加模型复杂度(换句话说,无论何时更精细地(harder)拟合数据),训练误差都趋于下降.然而过度的拟合,模型会自适应使得更加接近训练数据,但不能很好地进行推广(比如说,测试误差很大).正如式 (2.46) 的最后一项,在这种情形下,预测值 f^(x0)\hat{f}(x_0)f^(x0) 的方差较大.相反地,如果模型不是特别的复杂,会 欠拟合 (underfit) 且有较大的偏差,也导致不能很好地泛化.在第 7 章中,我们考虑估计预测方法的测试误差的各种方式,并因此在给定的预测方法和训练集下,估计出最优的模型复杂度.
个人解读本章不同于2.5节从最小二乘的角度解读泛化误差,而是采用k近邻的方法代入泛化误差公式,最后解读出k近邻情况下的诸多结论,而这些结论其实代表了一种普遍现象,对其他的模型结论亦是如此(例如图2.11)。
作者:Nstar-LDS