算法之路-模拟退火(Simulated Annealing)-Python实现
退火是材料工程领域的术语,为一种热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却的过程,可以达到降低硬度,细化晶粒,调整组织,消除组织缺陷等目的。
模拟退火算法的由来模拟退火算法的思想借鉴于上面提到的退火原理,固体温度很高时,内能较大,内部粒子处于快速无序运动;而在温度缓慢降低的过程中,固体的内能减小,粒子趋于有序,最终当固体处于常温时,内能最小,此时内部粒子也最为稳定。
在解决最优化问题的过程中,借鉴退火的思想,我们要设计这样一个算法:
现在把数据集想象成我们要热处理的固体。
首先我们给数据集“加温”,使其处于一个无序的状态,此时我们可以获得问题的最优化问题的初始解;接下来人为的制造一个扰动量来使数据集进入一个新状态,来模拟固体在环境中无序运动的过程,当然,也许由于某种原因,这个固体的状态并没有朝着我们想要的方向转化,因此每一次都需要我们根据最优化问题的目标函数来决定这个固体是否要向新状态转化;当我们确定这样一个状态后,便可以看作数据集获得了当前温度下的最优解,现在便可以开始降温,在下一个温度继续迭代上述过程;最终,数据集降温到了一定的温度,我们也得到了模拟退火算法处理的结果。
上面我们提到了要给数据集制造扰动使其获得一个新的状态,在算法的实现过程中,由邻域函数来完成这项任务。
这里先说明状态空间的概念,状态空间也称为搜索空间,实际上就是所有可行解的集合。
为了能够让我们的数据集处于一个足够无序的状态可以尝试每一种可行解,这就要求邻域函数应产生的候选解应该可以遍布整个状态空间。领域函数通常由产生候选解的方式和候选解产生的概率分布组成,而候选解一般按照某一概率密度函数对解空间进行随机采样获得。
数据集找到了一个新的状态,要不要转化呢?这由状态转移概率来决定。模拟退火算法中往往根据Metropolis准则来确定状态转移概率,其数学表达式如下:
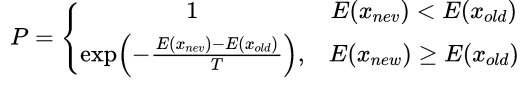
式中出现的TTT可以理解为当前环境的温度,随着退火的不断进行,这个参数不断减小。**这里可以思考这样一个相对比较细致的问题,随着温度的不断降低,我们接受一个新状态的可能性是变大了还是变小了?**根据这个问题也许能体会到某些算法细节设计的精妙之处。
为了模拟固体的降温过程,需要给定一个时间函数来买描述某一时刻的温度。不同的模拟退火算法用到的降温方式不同,但是大同小异,这里选择快速模拟退火算法的降温方式,其时间函数如下:
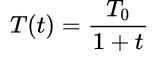
初始温度T0T_0T0会直接影响获得解的质量,同时也会影响程序的执行时间,两者呈现制约关系。为了能够在效率和结果之间进行一个平衡,这里采用下述方法确定初始温度:
随机产生一组(多个)状态,确定每两个状态间的最大目标值差,然后根据差值,利用下面的函数确定初始温度,其中PrPrPr称作初始接受概率。
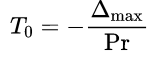
根据上述对算法的整体描述,不难发现存在两层循环,内循环用来模拟每个温度下状态的稳定,而外循环用来模拟整体的降温过程。
内循环的终止条件应该是当前温度下的状态达到稳定,而外循环的终止条件是整个系统的熵已经趋于稳定,当然对于相对简单的数据集,可以牺牲掉部分执行效率,直接规定循环次数。
旅行商问题(Traveling Salesman Problem)具体描述如下:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。 TSP问题是组合优化中的一个NP困难问题,在计算机以及运筹学有着很重要的地位。
数据集的准备这里提供的数据集给出了每个城市的坐标,需要编写计算两点间距离的函数进行转化。
模拟退火算法代码实现(Python) 编写一些必要的函数 load_data(file_name)数据读取函数此函数用来读取数据集中的坐标数据。
存储数据集的txt文件每行存储两个数,代表一个城市的坐标值,两个数之间用空格隔开。整体思想就是先将其读入pandas.DataFrame数据类型中,利用split(’ ')函数进行分割处理。
def load_data(file_name):
datas = pd.read_table(file_name, sep='\t', header=None)
datas.columns = ['coordinate']
points = pd.DataFrame(columns=['x', 'y'])
for i in range(len(datas)):
values = datas['coordinate'][i].split(' ')
points = points.append(pd.DataFrame({'x': float(values[0]), 'y': float(values[1])}, index=[i]))
return points
cal_distance(x1, x2, y1, y2)两点间距离计算函数
此函数用来计算两点之间的欧氏距离。
def cal_distance(x1, x2, y1, y2):
return math.sqrt((x1-x2)**2+(y1-y2)**2)
cal_total_length(points, path, start, end)路径长度计算函数
此函数用来计算给定路径的总距离,给定城市坐标集、特定路径、起点和终点,函数返回计算结果。
def cal_total_length(points, path, start, end):
length = 0
n = 1
for i in range(len(path)):
if i == 0:
length += cal_distance(start[0], points['x'][path[i]], start[1], points['y'][path[i]])
n += 1
elif n < len(path):
length += cal_distance(points['x'][path[i]], points['x'][path[i+1]], points['y'][path[i]], points['y'][path[i+1]])
n += 1
else:
length += cal_distance(points['x'][path[i]], end[0], points['y'][path[i]], end[1])
return length
random_to_list(datas)乱序函数
此函数用来模拟无序运动,即随机打乱数据集中城市坐标的顺序。
def random_to_list(datas):
return list(np.random.permutation(datas))
simulated_annealing_tsp(points, pr, p_back, mk)模拟退火算法执行函数
此函数为模拟退火算法的执行函数,对数据集进行模拟退火过程。传入的四个参数分别为坐标集合、初始接受概率、重升温概率以及内循环次数设置参数。
默认起点和终点均为数据集中的第一个坐标值点,为了计算方便,先将其从坐标集中去掉,模拟退火完成后再补充该点即可。
计算初始温度T0T_0T0,根据之前提到的计算方法,随机产生路径,计算得到确定每两个状态间的最大目标值差,再根据初始接受概率确定初始温度,这一部分的代码如下:
delt_max = 0
for i in range(10):
random_path1 = random_to_list(path)
random_path2 = random_to_list(path)
length1 = cal_total_length(points, random_path1, start, end)
length2 = cal_total_length(points, random_path2, start, end)
delt_max_temp = abs(length1 - length2)
if delt_max_temp >= delt_max:
delt_max = delt_max_temp
T0 = delt_max / pr # 设置初始温度
simulated_annealing_tsp(points, pr, p_back, mk)函数整合如下:
def simulated_annealing_tsp(points, pr, p_back, mk):
start = list(points.iloc[0])
end = list(points.iloc[0])
points = points.drop([0])
points.index = [i for i in range(len(points))]
path = [i for i in range(len(points))] # 给定一个初始化路径
# 随机产生路径序列,根据初始温度计算公式计算找到最优的初始温度
delt_max = 0
for i in range(10):
random_path1 = random_to_list(path)
random_path2 = random_to_list(path)
length1 = cal_total_length(points, random_path1, start, end)
length2 = cal_total_length(points, random_path2, start, end)
delt_max_temp = abs(length1 - length2)
if delt_max_temp >= delt_max:
delt_max = delt_max_temp
T0 = delt_max / pr # 设置初始温度
T = T0
Tmin = T / 100
k = mk * len(path) # 内循环次数
t = 0 # 用于记录当前轮次
path = random_to_list(path)
length = cal_total_length(points, path, start, end)
print('The distance of the random path is {:.2f}.'.format(length))
while T > Tmin:
for i in range(k):
new_path = path
for j in range(int(T0 / 500)):
a = 0
b = 0
while a == b:
a = np.random.randint(0, len(path))
b = np.random.randint(0, len(path))
te = new_path[a]
new_path[a] = new_path[b]
new_path[b] = te
new_length = cal_total_length(points, new_path, start, end)
if new_length < length:
length = new_length
else:
p = math.exp(-(new_length - length) / T)
r = np.random.uniform(low=0, high=1)
if r = 1-p_back:
T = T * 2
continue
t += 1
print('The t={} runs is over.'.format(t))
T = T0 / (1 + t)
path.insert(0, -1) # 插入起点,路径序列值置为-1
return length, path
测试代码
if __name__ == '__main__':
file_name = 'data_simulated_annealing_100.txt'
points = load_data(file_name)
ticks_begin = time.time()
length, path = simulated_annealing_tsp(points=points, pr=0.5, p_back=0.15, mk=10)
ticks_end = time.time()
print('Time cost is {:.2f}s.'.format(ticks_end-ticks_begin))
print('The distance of the shortest path is {:.2f}.'.format(length))
points['path'] = path
points_order = points.sort_values(by=['path'])
plt.plot(points_order['x'], points_order['y'])
plt.title('The Optimal Path of Datas from {}'.format(file_name))
plt.show()
 sunzhihao_future
sunzhihao_future
 原创文章 12获赞 28访问量 6421
关注
私信
展开阅读全文
原创文章 12获赞 28访问量 6421
关注
私信
展开阅读全文
作者:sunzhihao_future