【时空序列预测第五篇】Memory In Memory: A Predictive Neural Network for Learning Higher-Order Non-Stationarity
最近在忙些别的,忙完之后要开始自己的paper计划了,这些文章都很有趣,读完感觉在家憋着也不那么难受了。
接下来保持住节奏,每周起码一篇paper reading,要时刻了解研究的前沿,是一个不管是工程岗位还是研究岗位AIer必备的工作,共勉!
一、Address这是cvpr2019年的一篇paper,依然来自于清华的团队
Memory In Memory: A Predictive Neural Network for Learning Higher-Order
Non-Stationarity from Spatiotemporal Dynamics
https://arxiv.org/abs/1811.07490v2

代码地址:
https://github.com/Yunbo426/MIM
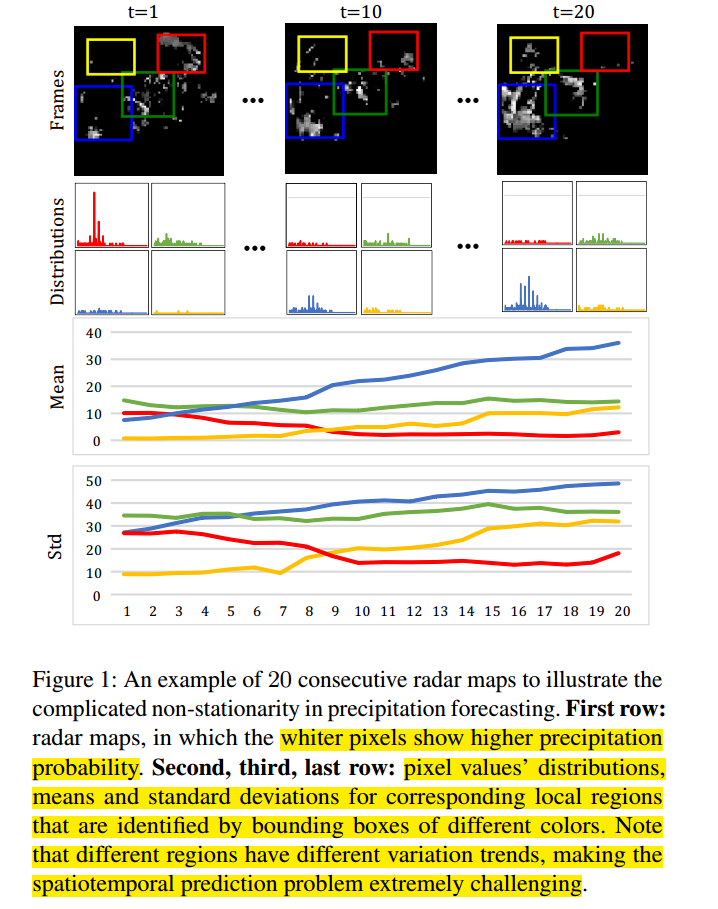
数据中存在平稳信息与非平稳信息,但主要的难点在于非平稳的预测,因为非平稳基本上是没有规律的,而平稳的信息是存在一定的周期或者规律不变的变换的。

存在一个很简单的例子让你理解

低阶的非平稳性:区域像素点的空间和时间的关系,即小块区域的时空变换。
高阶的变化:例如在气象中的雷达回波图中对应的数据的堆积、变形或耗散,即整体的变换趋势,更为复杂。
如下图。
文中的巧妙以及想法的来源取决于此:

任何一个非平稳过程都可以分解为:确定项+时间变量多项式+零均值随机项
而通过差分的操作,我们可以把时间变量多项式转换成一个常量,使确定性的组成部分可预测。这里引入了差分。

大多数的经典时间序列分析也都是假设通过差分的转换方式把非平稳趋势近似的转换为平稳项,继续说明差分的可靠性,比如ARIMA。

对于LSTM有三个门,忘记门,输入门,和输出门,而忘记门是和过去的状态最密切的gate。

文中下面的这个发现也认定的这点可以多加观察

在模型的工作过程中,忘记门有百分之80都处于饱和状态,即意味着state的传播是一个时不变的传播,也就是忘记门在工作的时候总是记住平稳的变换信息。
这里近似可以看作对于整个的预测就是个类似于线性的推理,因为经过忘记门的state是不变的,基本上可以说预测只取决于输入,而取决于先前的信息也是固定的。
过度的差分还有个缺点就是会让整体的信息丢失太多,所以文中也给出解释:(这也是为什么只用忘记门的原因之一)

差不多三个方面,提出了一个state 连接可以提取到高阶非平稳特征,一个新的RNN结构,以及进行stacking MIM blocks带来的更好的效果。


首先你要能把这张图捋明白,如果看不懂建议看我的第三篇文章,左边是ST-LSTM结构,右边是更改的。
主要更改内容在于forget gate区域。
这里需要理解一下为什么下面叫做非平稳(N),上面的叫作平稳(S),因为前面的例子钟说了,ST-LSTM中的忘记门基本是饱和的,所以它基本上只获取了平稳的信息,而整个直接联系就是C状态值,再加上下面的输入为差分,而差分的转换其实就是非平稳的信息,所以上为S,下为N。
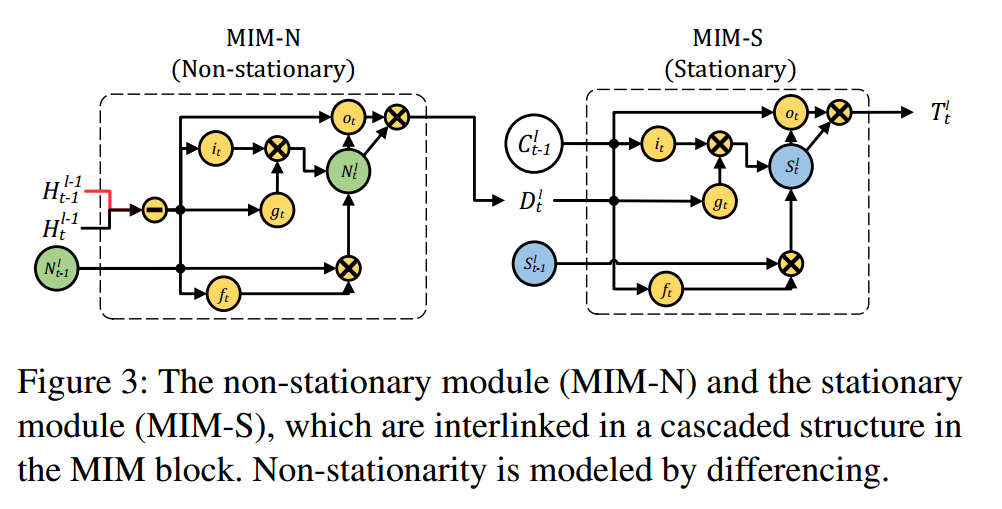
分析一下整个结构其实不是很复杂,主要大家一步一步看,其实就是近似于于两个LSTM的级联结构,只是第一个输入是一个差分,第二个输入是第一个的输出。公式如下: 主要大致区别希望读者自己去捋一下,要不讲起来实在太墨迹了,我这边帮忙标注:
MIM-N

其实这两个结构一起做的事就是第一个结构提取出非平稳信息,之后传递给第二个结构,第二个结构利用门控来选择是否忘记和记住多少的非平稳信息或者memory cell(C)即近似的平稳信息。
如果差分信息消失了,说明非平稳信息不是很显著的,那最终的输出依然还是C,即原始的memory cell,反之不赘述了。
所有的公式如下:

这里的这个比喻我觉得恰到好处,大家可以感受一下:

进行stacking多层MIM blocks,会让模型能够更好的学到更多高阶的非平稳特征。
因为差分的输入为左下方的hidden state,所以这种结构不能存在于第一层,即第一层还是利用ST-LSTM。
这里也再次说明了为什么要stacking的理论依据,因为可以通过不过的差分,使得非平稳项得阶次降低,从而更好的预测。

结构示意图为
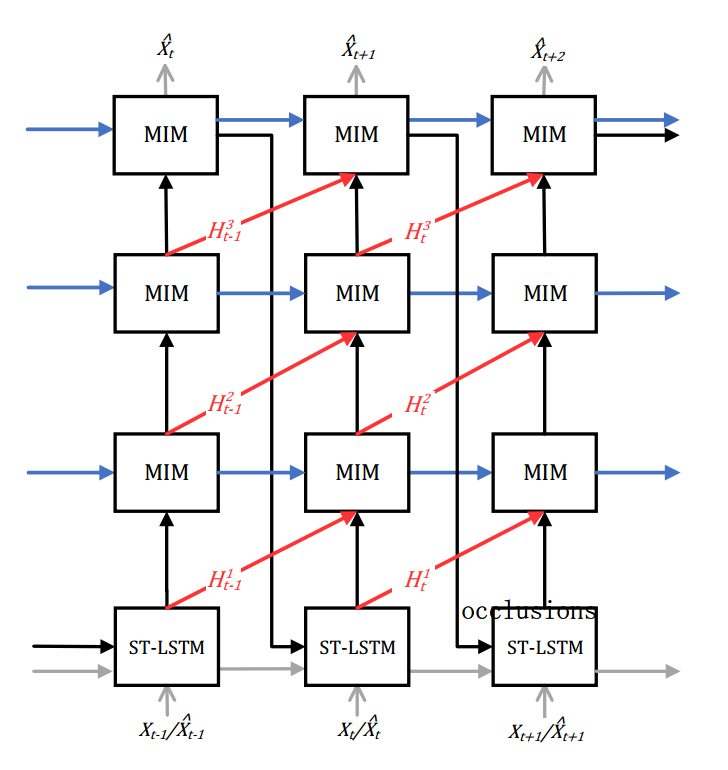

这里非常清楚得表达了,我不赘述了,唯一强调的就是这里的推测策略是我们平时经常用到的,这里的示意图画的还是很全面得,对于输入可以是此时的一个输入序列,也可以是上一个时刻得输出,即你可以做序列预测序列的类似于端到端的预测,也可以先预测一个时刻的,之后把此时刻的当作真实值输入预测下一个时刻,如此下去。。
简易公式如下:

模型参数:一共四层,第一层是ST-LSTM,其余三层为MIM,MIM的feature channel为64,利用l2损失,ADAM optimizer,lr为0.001,利用了两个trick,为layer nomalization和scheduled sampling,具体见开源代码。
4.1 Moving MNIST
清晰可见后两个更好一些,没有出错的预测,也更加清晰,模糊程度低些。

注意看标黄的地方,全篇提出的是一个MIM机制,这个机制同样适用于其他时空序列的LSTM结构中即是通用的,改变方式就是将结构中的forget gate进行修改,最终表现效果也很好。
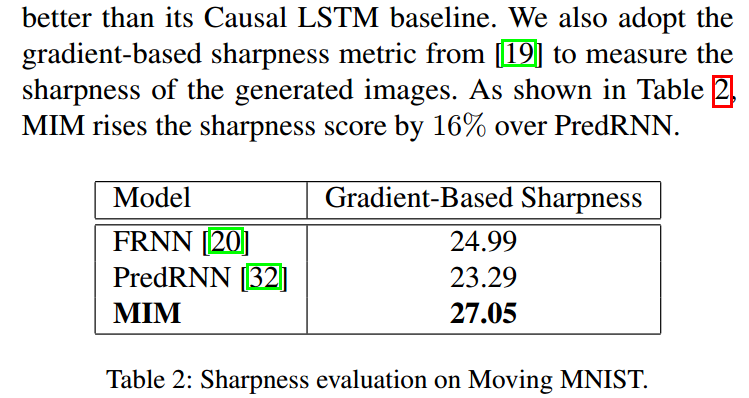
通过这个实验说明MIM可以让图片更加的sharpness,不模糊有的时候对于时空序列预测问题是一个更关键的问题。
到这里大家有没有个疑问,每篇一问又开始了!如果MIM-N与MIM-S两个分别存在的时候呢?是什么效果。

文中做了实验表明两个都存在的时候,表现最好。
文中也对block的数量进行了实验得出了结论。

这里也对忘记门的情况做了实验,忘记门的饱和情况,大多数的忘记门值为0

这里的解释我十分赞同,我个人感觉解释的很棒。

就是说短期的非平稳是很难被获取的,如果忘记门大多数是0的话,说明他一直在刷新,其实短期的信息是没有获得的。
而加入了MIM之后,饱和率的下降,说明更多的短期非平稳可以被传播,并且对于MIM-N主要处理的是短期的信息,而MIM-S主要处理的是长期的变化,为啥这么解释呢?因为时间序列问题长期的信息往往是有规律的也就是平稳的信息,而短期的往往是突发事件,或者很多非平稳的信息,这样就好理解了。
对于雷达数据集,其他数据集请自行观看。

最终的衡量标准。
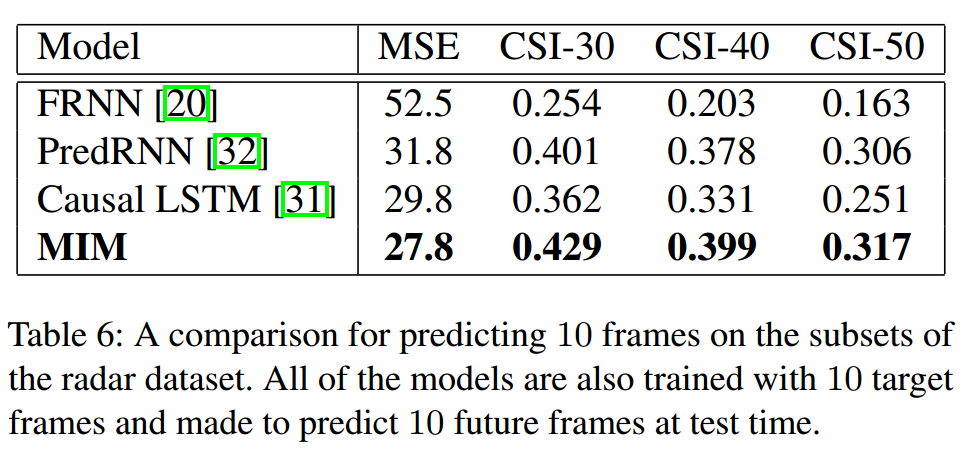
这里的 CSI是降水预测一个常用的指标,感兴趣的可以去查一下我这里也简单讲一下。
就是利用阈值将雷达回波图上的像素点的值化为0或者1。
之后算出对应的

通过CSI的公式可求出,对于阈值得选择的不同可以预示着你想主要预测的是小雨、中雨、还是大雨、暴雨

作者:AI蜗牛车