MATLAB之拉格朗日插值
1、插值问题的定义
当精确函数 y = f(x) 非常复杂或未知时,在区间【a,b】上一系列节点x0,x1,x2,......xn处测得函数值f(x0)、f(x1)、f(x2)......f(xn);
由此构造一个简单的简单易算的近似函数g(x)≈f(x),满足条件g(xi)=f(xi) (i=0,1,2...,n)。这个问题就被称为插值问题。
2、上一篇文章,我们介绍了多项式插值,现在我们来介绍一下拉格朗日插值。
问题引入:
n=1,一次拉格朗日插值(取两个点,插值多项式最高次数n=2-1=1)
已知点x0、x1及其函数值y0、y1,则根据多项式插值原理,可以确定一个次数不超过n-1(2-1)的代数多项式(n为插值点的个数)g(x)=a0+a1*x,使得g(x0)=y0,g(x1)=y1。其推导过程如下;

表达式最后的形式即为拉格朗日插值多项式的形式。
n=2,二次拉格朗日插值(取三个点,插值多项式最高次数n=3-1=2)
已知点x0、x1、x2及其函数值y0、y1、y2,则根据多项式插值原理,可以确定一个次数不超过n-1(3-1)的代数多项式(n为插值点的个数)g(x)=a0+a1*x+a2*x^2,使得g(x0)=y0,g(x1)=y1,g(x2)=y2。写成拉个朗日擦插值的形式为:

要使g(xi)=yi,其中Lk应满足Lk(xi)=1,k=i ; Lk(xi)=0 ,k≠i;根据Lk(x)的定义,xk以外所有的结点都是Lk(x)的根,因此

又由Lk(xk) = 1,得

将求得的系数带入即可求得二次插值的拉格朗日多项式
n次拉格朗日插值(取n+1个点,插值多项式最高次数n)
其拉个朗日多项式的形式为:

要使g(xi)=yi,其中Lk应满足Lk(xi)=1,k=i ; Lk(xi)=0 ,k≠i;根据Lk(x)的定义,xk以外所有的结点都是Lk(x)的根,因此
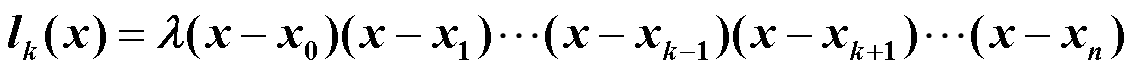

又由Lk(xk) = 1,得
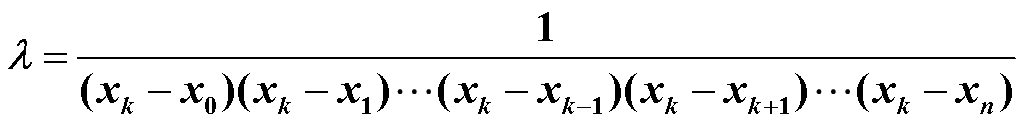
综上所述

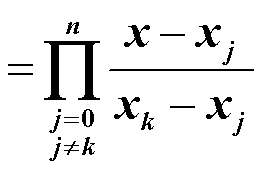
综上所述,我们有1次,2次,推导出来n次拉个朗日插值多项式的数学公式。
二、matlab代码
%% 拉格朗日插值 (创建函数脚本方可运行)
close
clc
clear
X=[2 3 5 7 8 9];
Y=[5 9 12 16 23 35];
function D=ji(X,n) %求拉格朗日多项式的系数子函数
syms x
%法一
% switch n
% case 1
% B=x-X(2:end);
% C=X(1)-X(2:end);
% case length(X)
% B=x-X(1:n-1);
% C=X(n)-X(1:n-1);
% otherwise
% B=x-X([1:n-1,n+1:end]);
% C=X(n)-X([1:n-1,n+1:end]);
% end
%法二
Xn=X(n);
X(n)=[];
B=x-X;
C=Xn-X;
D=prod(B)/prod(C);%prod数组元素连乘积
end
m=length(X);
for i=1:m
L1(i)=Y(i)*ji(X,i);
end
L=sym2poly(expand(sum(L1))) %将符号变量变为数据
x=X(1):0.1:X(end);
y=polyval(L,x); %y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值
plot(x,y) %画拟合曲线
hold on
plot(X,Y,'o') %画散点图
作者:天涯铭