matlab克里格插值(基于扇区邻域点选取)

Kaitlyn ·

更新时间:2024-11-13

· 957 次阅读

前言

此次博客是前面mink函数的博客的进阶版本，往往我们在进行克里格插值时需要计算目标点周围邻域内多个点来进行插值操作，一般情况下邻域内的点数并不是越多越好，有时要根据邻域内点的分布分布状况以及点的分布个数来评估克里格插值的结果，但是有时邻域的点对数量选取是基于距离最短的原则来选取，这样就有时会造成邻域点选取的结果分布不均匀，为了使插值更加精确，arcgis中已经封装了设置领域点选择的一些条件，如下图所示，arcgis中还考虑了扇区的数目，每个扇区内点的数量限制，潘老师的理解是把扇区的数目就是把整个区域搜索的圆分成nnn等份，如下图会有更直观的理解：

从上图中定义的扇区大小为4，则将其分为4等分，每个扇区至少要有4个相邻要素，最多8个，因此权重那里最少是16个，那么问题来了，怎样在Matlab中编程将每个扇区内这样的点对提取出来呢。

1方法原理 1.1坐标系平移

对于坐标点集(xi,yi)(x_i,y_i)(xi,yi),取出要搜索的目标点(x0,y0)(x_0,y_0)(x0,y0),剩余点集为(x0i,y0i)(x_{0i},y_{0i})(x0i,y0i),进行坐标平移，如下，新坐标系以(x0,y0)(x_0,y_0)(x0,y0)为原点，因此剩余点集坐标有：
x0i=x0i−x0y0i=y0i−y0 x_{0i}=x_{0i}-x_0\\ y_{0i}=y_{0i}-y_0 x0i=x0i−x0y0i=y0i−y0
如下图所示：
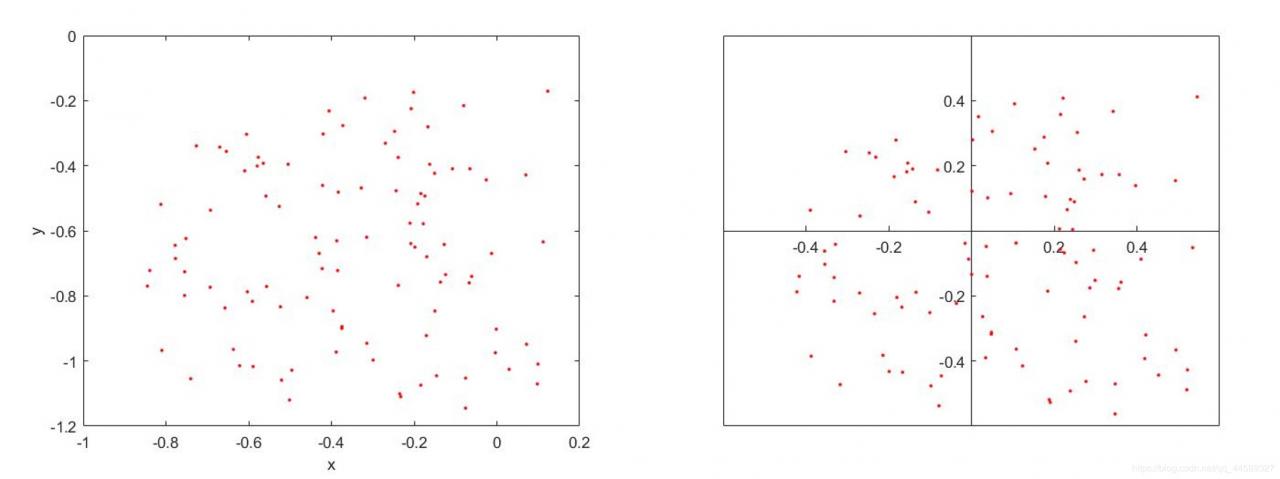
在这里插入图片描述

1.2方位角确定

方位角原本是在测绘中的一个定义，这里我们求解的平移坐标系之后的剩余点集与原点连线与正北方向即(y轴)(y轴)(y轴)的夹角α∈[0,2π]\alpha \in[0,2\pi]α∈[0,2π],在直角坐标系下有四个象限，具体如下图所示

因此有计算方位角公式如下：
αI=π2−arctan(yx),αIV=π2−arctan(yx)\alpha_{I}=\frac{\pi}{2}-arctan(\frac{y}{x}) ,\alpha_{IV}=\frac{\pi}{2}-arctan(\frac{y}{x})αI=2π−arctan(xy),αIV=2π−arctan(xy)
αIII=3π2−arctan(yx),αII=3π2−arctan(yx)\alpha_{III}=\frac{3\pi}{2}-arctan(\frac{y}{x}),\alpha_{II}=\frac{3\pi}{2}-arctan(\frac{y}{x})αIII=23π−arctan(xy),αII=23π−arctan(xy)
因此有如下通项公式：
α=π−π2sign(x)−arctan(yx)\alpha=\pi-\frac{\pi}{2}sign(x)-arctan(\frac{y}{x})α=π−2πsign(x)−arctan(xy)
其中sign(x)sign(x)sign(x)为符号函数，表达式如下：
f(x)=sgn(x)={ ⁣ ⁣1,x>00,x=0−1,x<0 f(x)= sgn (x)=\left\{ \!\! \begin{array}{cl} 1, & x>0 \\ 0, & x=0 \\ -1, & x<0 \end{array} \right. f(x)=sgn(x)=⎩⎨⎧1,0,−1,x>0x=0x<0

1.3邻域点扇区确定

记αi\alpha_{i}αi为第iii个点的方位角，areaiarea_{i}areai为其所属扇区，nnn为扇区数目，因此第iii个扇区的角度范围是[(i−1)∗2πn,i∗2πn][(i-1)*\frac{2\pi}{n},i*\frac{2\pi}{n}][(i−1)∗n2π,i∗n2π]
因此有如下计算公式：
areai=ceil(α/(2π/n)) area_{i}=ceil({\alpha}/({2\pi/n})) areai=ceil(α/(2π/n))

2案例实践 2.1数据集

随机产生100个[0,1]直接的随机坐标点，存储与txt文档中，

设置扇区数目nnn
每个扇区对应最少要素数目numneighborminnum_{neighbormin}numneighbormin
每个扇区对应最多要素数目numneighbormaxnum_{neighbormax}numneighbormax

2.2坐标系平移

xy=textread('C:\Users\asus\Desktop\3.txt');
xy0=xy(1,:);%这里默认将第一个点选定目标点
xy1=xy(2:end,:);%目标点周围的所有点
xy1=[xy1(:,1)-xy0(1),xy1(:,2)-xy0(2)];%平移坐标系，使目标点为原点
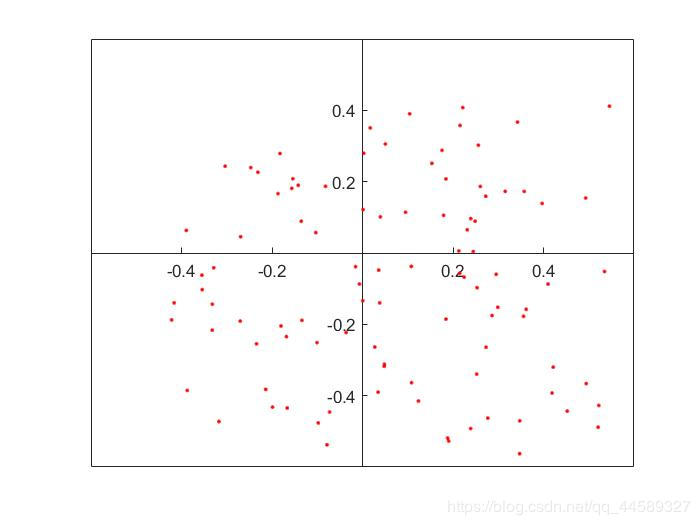
plot(xy1(:,1),xy1(:,2),'r.');%绘图
xlabel('x');ylabel('y');
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';%设置坐标系为原点处

最终效果如下图：

2.3方位角计算与扇区确定

n=6;%扇区数目
num_neighbormin=4;%设置每个扇区内要搜索到的点的数量限制
num_neighbormax=8;%
%最少搜索4个，最多8个
%计算目标点周围的点方位角
angle=pi-(pi/2).*sign(xy1(:,1))-atan(xy1(:,2)./xy1(:,1));%这里返回的弧度值
xy_area=[xy1,ceil(angle./(2*pi/n))];%第1，2列为对于的xy坐标数据，
%第三列为对应坐标点对在哪个扇区

2.4针对每个扇区开始搜索

%开始逐个扇区搜索
I=cell(n,1);%定义一个扇区大小的元胞，存储对应扇区的结果
for i=1:n
    logi=xy_area(:,3)==i;%第i个扇区内所有点
    xy_area_i=xy_area(logi,:);
    D2=(xy_area_i(:,1)).^2+(xy_area_i(:,2)).^2;
    num=size(xy_area_i,1);
    if num>num_neighbormax
        num_neighbor=num_neighbormax;
    elseif num>num_neighbormin
        num_neighbor=num;
    else
        I{i,1}=[];
        continue;
    end
    [D,tag]=mink(D2,num_neighbor);%tag表示最近的4个点D表示对应的距离平方
    Dc_neighbor=sqrt(D);%最近的num_neighbormax个点距离
    tag_neighbor=tag;%最近的num_neighbormax个点的索引
    I{i,1}=xy_area_i(tag_neighbor,:);
end

首先定义一个大小与扇区数目的元胞存储每个扇区的结果点的坐标，其次在各个扇区上搜索的邻域点数目判断，再基于前面博客所写的mink函数的基础知识上进行结果存储
条件判断如下：
1.如果搜索到的点数大于最大数的限制，那么取前numneighborminnum_{neighbormin}numneighbormin个点作为邻域点
2.如果在其范围之间，那么就用搜索到的点数
3.如果搜索到的点数小于最小数的限制，那么之间返回空值，进行下一个扇区的搜索

2.5结果展示

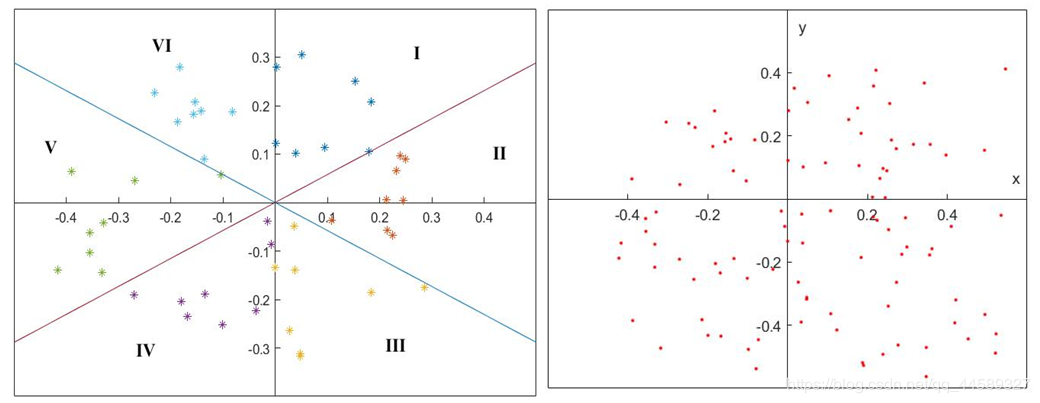
figure;%画六个扇区的散点，不同颜色表示
for i=1:n
    plot(I{i,1}(:,1),I{i,1}(:,2),'*');
    hold on;
end
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
ux=-0.5:0.001:0.5;
uy1=ux./(tan(2*pi/n));
uy2=ux./(tan(2*2*pi/n));
hold on;
plot(ux,uy1);
hold on;
plot(ux,uy2);

效果如下：
在这里插入图片描述

3总结

本次matlab克里格插值(基于扇区邻域点选取)的方法是基于Arcgis中的功能模块来设置，最终将目标的点对筛选出来再次进行下一步操作才能进行克里格插值的计算，因此在考虑邻域点的空间分布的情况下来对其进行克里格插值是提高精度的一种方法，希望同学们能够将简单的算法原理进一步转化成代码能够实现功能，走进算法世界，展现代码力量！！

4参考文献

[1]王红芳,张保亮.坐标方位角通用计算公式[J].山西建筑,2008(06):361-362.

5附录

xy=textread('C:\Users\asus\Desktop\3.txt');
xy0=xy(1,:);%这里默认将第一个点选定目标点
xy1=xy(2:end,:);%目标点周围的所有点
xy1=[xy1(:,1)-xy0(1),xy1(:,2)-xy0(2)];%平移坐标系，使目标点为原点
plot(xy1(:,1),xy1(:,2),'r.');%绘图
xlabel('x');ylabel('y');
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
n=6;%扇区数目
num_neighbormin=4;%设置每个扇区内要搜索到的点的数量限制
num_neighbormax=8;%
%最少搜索两个，最多4个
%计算目标点周围的点方位角
angle=pi-(pi/2).*sign(xy1(:,1))-atan(xy1(:,2)./xy1(:,1));%这里返回的使弧度值
xy_area=[xy1,ceil(angle./(2*pi/n))];%第1，2列为对于的xy坐标数据，
%第三列为对应坐标点对在哪个扇区
%开始逐个扇区搜索
I=cell(n,1);%定义一个扇区大小的元胞，存储对应扇区的结果
for i=1:n
    logi=xy_area(:,3)==i;%第i个扇区内所有点
    xy_area_i=xy_area(logi,:);
    D2=(xy_area_i(:,1)-xy0(1)).^2+(xy_area_i(:,2)-xy0(2)).^2;
    num=size(xy_area_i,1);
    if num>num_neighbormax
        num_neighbor=num_neighbormax;
    elseif num>num_neighbormin
        num_neighbor=num;
    else
        I{i,1}=[];
        continue;
    end
    [D,tag]=mink(D2,num_neighbor);%tag表示最近的4个点D表示对应的距离平方
    Dc_neighbor=sqrt(D);%最近的num_neighbormax个点距离
    tag_neighbor=tag;%最近的num_neighbormax个点的索引
    I{i,1}=xy_area_i(tag_neighbor,:);
end
figure;
for i=1:n
    plot(I{i,1}(:,1),I{i,1}(:,2),'*');
    hold on;
end
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
ux=-0.5:0.001:0.5;
uy1=ux./(tan(2*pi/n));
uy2=ux./(tan(2*2*pi/n));
hold on;
plot(ux,uy1);
hold on;
plot(ux,uy2);

作者：you_are_mine_py

插值 matlab

1024 个赞