ASR 隐马尔可夫模型(HMM)
马尔可夫模型(HMM)是表达常用的数学模型,相关概念在随机过程中能学到。在语音识别(ASR)中,是基础且重要的模型之一。本篇文章主要介绍:
HMM 概念 前向和后向算法 维特比算法 隐马尔可夫模型(HMM) 简单理解HMM数据科学中,预测是一个经久不衰的问题。以常见的时间为序数据为例,数据科学家期望对过去(t0t_{0}t0时刻)和当前(tNt_{N}tN时刻)数据的观察( Time ),实现预测未来(tN+1t_{N+1}tN+1时刻)的值,HMM也是为了干这类事情而生的统计模型。
做个不恰当但有意思的比喻,假设数据科学家是算命先生,观察到的数据是求富贵顾客的生辰八字、面相等等。中式算命先生掏出周易算本(统计模型),输入观察数据,得出结果——顾客会富贵。这么个过程就是数据科学常干的事,HMM也是为了干类似的事情而生的统计模型(想象成周易算本)。
分享其它博主拿HMM干的事:
1、预测女朋友心情
现在回到HMM,实际HMM或者其它统计学方法能干的不止这些,包括分类、数据压缩等都是常见任务。通过概率的表达,HMM大多用于时间序列的模型,预测天气、股票等。HMM的主要机理由内部状态节点实现,包含各节点之间的转移概况,以及各状态与实际观测结果之间的观测概率。或者,换个方式理解转移概率和观测概率,转移概率代表数据变化主要趋势,观测概率包含可能的观测与主趋势差异。通过不断输入观测数据的训练,最终转移概率能把握数据随时间的主要变化规律,从而实现下一时刻的预测。因为模型内部的状态是不可观测,所以是“隐”(Hidden)。
HMM三大基本问题:
概率计算问题:已知模型参数和观测值,计算观测值的概率; 预测问题:已知模型和观测值,计算观测值概率最大时,随时间变化的状态路径; 学习问题:已经观测值,估计使观测值概率最大的模型。 图解HMM流程先介绍盒子和球的例子:假设有三个盒子,盒子里都有红球和白球,每次观测选取一个盒子取一个球。根据以上介绍,HMM模型参数在例子中表示如下表
| 模型参数 | 参数值 | 概率表达 | 意义 |
|---|---|---|---|
| 状态集合 | 【1号盒子,2号盒子,3号盒子】 | HMM的状态节点 | |
| 状态转移概率 | A=[a12a22a32a12a22a32a13a23a33] A = \begin{bmatrix} a_{12} & a_{22} & a_{32} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{bmatrix} A=⎣⎡a12a12a13a22a22a23a32a32a33⎦⎤ 1、2、3对应盒子号 | aij=P(Statet+1=Statej∥Statet=Statei)a_{ij}=P(State_{t+1}=State_{j} \| State_{t}=State_{i})aij=P(Statet+1=Statej∥Statet=Statei) | 当前时刻(ttt)到下一时刻(t+1t+1t+1)时的状态转移概率 |
| 状态初始概率 | π=[π1,π2,π3]\pi=[\pi_{1},\pi_{2},\pi_{3}]π=[π1,π2,π3] | πi=P(Statet=0=Statei) \pi_{i}=P(State_{t=0}=State_{i}) πi=P(Statet=0=Statei) | 初始时刻,取到各个状态的概率 |
| 观测集合 | 【红,黄】 | viv_{i}vi | 所有可能的观测结果 |
| 状态观测概率 | B=[b1Redb1Yellowb2Redb2Yellowb3Redb3Yellow] B = \begin{bmatrix} b_{1Red} & b_{1Yellow} \\ b_{2Red} & b_{2Yellow} \\ b_{3Red} & b_{3Yellow} \end{bmatrix} B=⎣⎡b1Redb2Redb3Redb1Yellowb2Yellowb3Yellow⎦⎤ Red、Yellow对应球颜色 | bij=P(Ot=vj∥Statet=Statei)b_{ij}=P(O_{t}=v_{j}\|State_{t}=State_{i})bij=P(Ot=vj∥Statet=Statei) | 每个状态的前提下,观测到每个结果的概率 |
| 观测值 | O=[Red,Red,Yellow] O = [Red, Red,Yellow]O=[Red,Red,Yellow] | 时间序列,记录多次观测到的结果 |
HMM模型示意图如下:
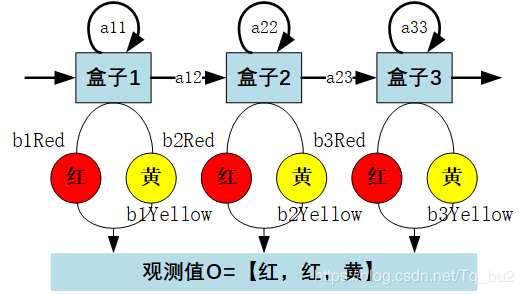
注意:a11a_{11}a11等,是当前时刻(ttt)到下一时刻(t+1t+1t+1)时的状态转移(此刻1中拿球,下一刻还是1中 拿球)概率。b1Redb_{1Red}b1Red等,是状态1观察为红(盒子1中拿出红球)的概率。
现在,假设HMM模型已知(如例子中展示的),包含状态转移概率矩阵A、状态观察概率B、状态初始概率π\piπ,组合成的模型记作H=(A,B,π)H=(A,B,\pi)H=(A,B,π)。现在求取到观测值O=[Red,Yellow,Red]O=[Red,Yellow,Red]O=[Red,Yellow,Red]的概率P(O∣H)P(O|H)P(O∣H)。
粗暴的求解思路:
找出可形成观测值O的所有情况,即每个时刻得到观察值的所有可能状态序列。或者说,每次取球时,从盒子取到该观察球色的所有可能性,记作III。 计算每种情况的概率,P(O,Ii∣H)P(O,I_{i}|H)P(O,Ii∣H) 所有情况概率求和得到最终观察值的概率,P(O∣H)=∑i=1IP(O,Ii∣H)P(O|H)=\sum_{i=1}^{I}P(O,I_{i}|H)P(O∣H)=∑i=1IP(O,Ii∣H)粗暴求解思路需要找到所有可能情况,复杂度是O(TNT)O(TN^{T})O(TNT),显然复杂度严重影响方法的实现与应用。为此,常使用的算法是前向算法与后向算法,讲复杂度降至O(TN^{2})。
作者:Charles Tu