机器学习之逻辑回归

Xena ·

更新时间:2024-09-21

· 816 次阅读

1、逻辑回归概念

面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别。它就是通过拟合一个逻辑函数（logit fuction）来预测一个事件发生的概率。所以它预测的是一个概率值，自然，它的输出值应该在0到1之间。–计算的是单个输出
那是什么手段让逻辑回归只能输出两种值呢？答：Sigmoid函数。

2、Sigmoid函数

我们先来看看之前一章说的线性回归，线性假设函数为：
hθ(x)=θ0+θ1x1+θ2x2+...+θnxn=θTxh_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}=\theta ^{T}xhθ(x)=θ0+θ1x1+θ2x2+...+θnxn=θTx
线性假设函数的输出是个没有范围的连续值，不适合分类问题。因此在线性回归的假设函数外包裹一层Sigmoid函数，使之取值范围属于(0,1)，完成了从值到概率的转换。逻辑回归的假设函数形式如下：
hθ(x)=g(θTx)=11+e−θTx=P(y=1∣x;θ)h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}=P(y=1|x;\theta )hθ(x)=g(θTx)=1+e−θTx1=P(y=1∣x;θ)
其中g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}}g(z)=1+e−z1
g(z)g(z)g(z)被称为Sigmoid函数。若P(y=1∣x;θ)=0.7P(y=1|x;\theta )=0.7P(y=1∣x;θ)=0.7，表示输入x时，y=1的概率为70%。
下图为Sigmoid函数图像:
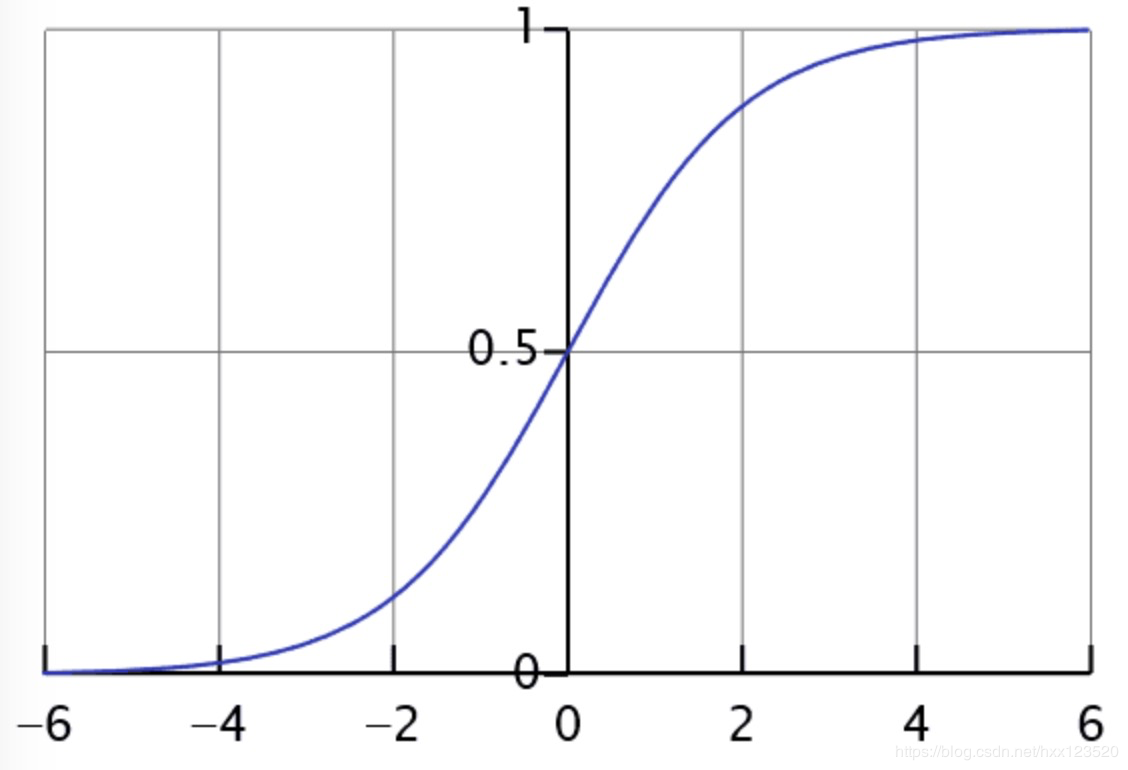在这里插入图片描述从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，当z为0时取值为12\frac{1}{2}21，在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要。

3、判定边界

我们现在再来看看，为什么逻辑回归能够解决分类问题。这里引入一个概念，叫做判定边界，可以理解为是用以对不同类别的数据分割的边界，边界的两旁应该是不同类别的数据。
举几个例子，如下：
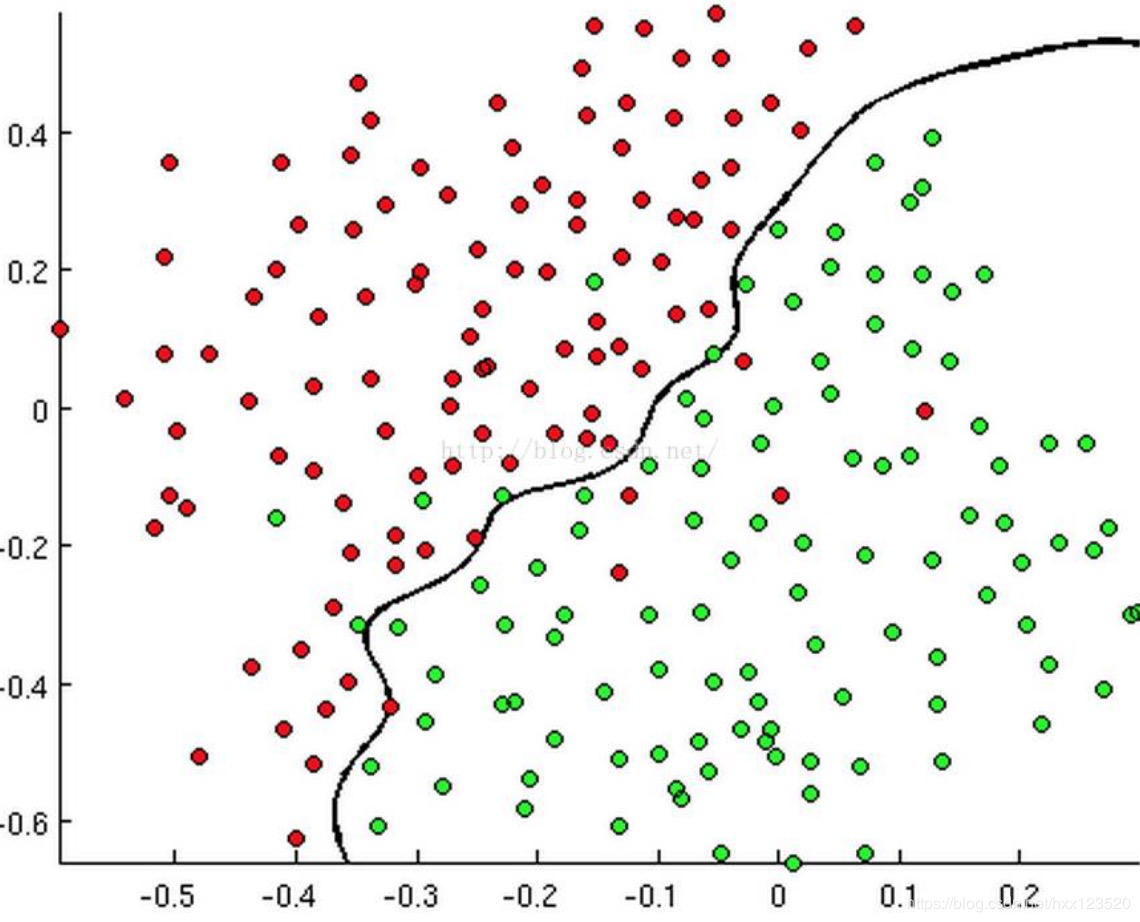在这里插入图片描述有时候是这个样子：
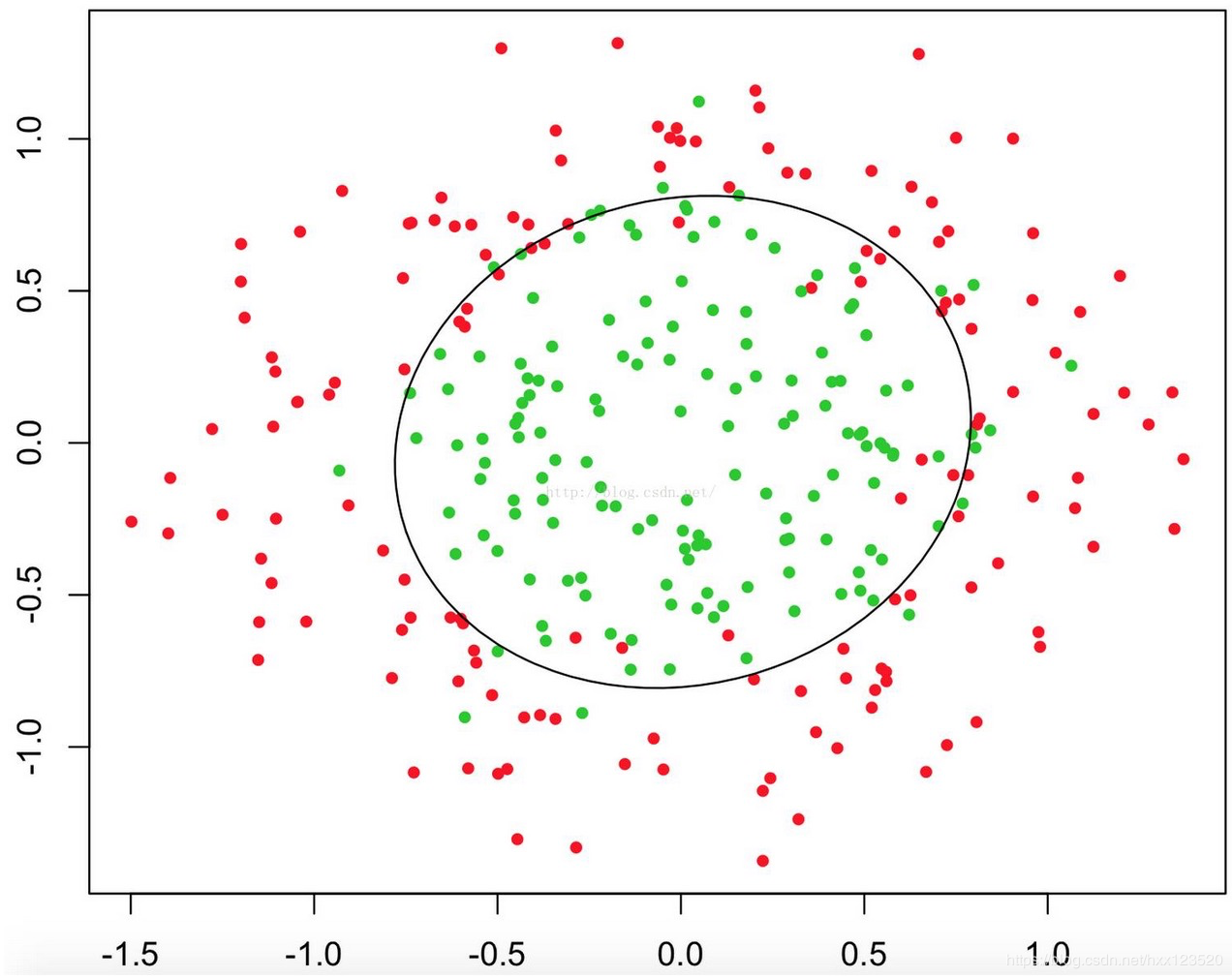甚至可能是这个样子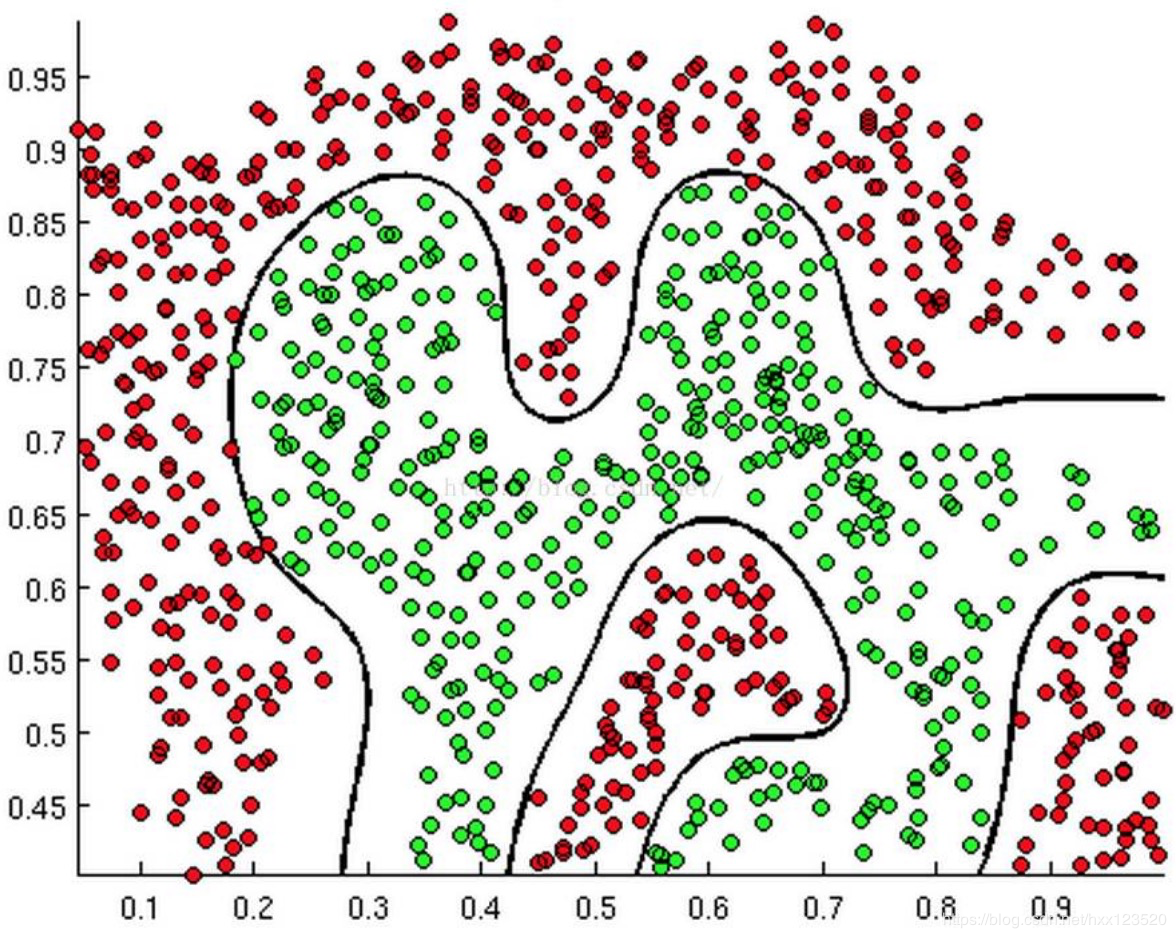：上述三幅图中的红绿样本点为不同类别的样本，而我们划出的线，不管是直线、圆或者是曲线，都能比较好地将图中的两类样本分割开来。这就是我们的判定边界，下面我们来看看，逻辑回归是如何根据样本点获得这些判定边界的。

通过sigmoid函数图像我们发现：
当g(z)⩾0.5g(z)\geqslant 0.5g(z)⩾0.5时，z⩾0z\geqslant 0z⩾0；hθ(x)=g(θTx)⩾0.5h_{\theta }(x)=g(\theta ^{T}x)\geqslant 0.5hθ(x)=g(θTx)⩾0.5，也就是说θTx⩾0\theta ^{T}x\geqslant 0θTx⩾0此时预估y=1；
反之，当y=0时，θTx<0\theta ^{T}x< 0θTx<0；
所以我们认为θTx=0\theta ^{T}x= 0θTx=0就是一个决策边界，当它大于或者小于0时，逻辑回归模型分别预测不同的分类结果。

我们先来看看第一个例子hθx=g(θ0+θ1x1+θ2x2)h_{\theta }x=g(\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2})hθx=g(θ0+θ1x1+θ2x2),其中θ0,θ1,θ2\theta _{0},\theta _{1},\theta _{2}θ0,θ1,θ2分别取值-3，1，1。则−3+x1+x2⩾0-3+x_{1}+x_{2}\geqslant 0−3+x1+x2⩾0时，y=1；则x1+x2=3x_{1}+x_{2}=3x1+x2=3是一个决策边界，图形表示如下，刚好把图像的两类点区分开来：
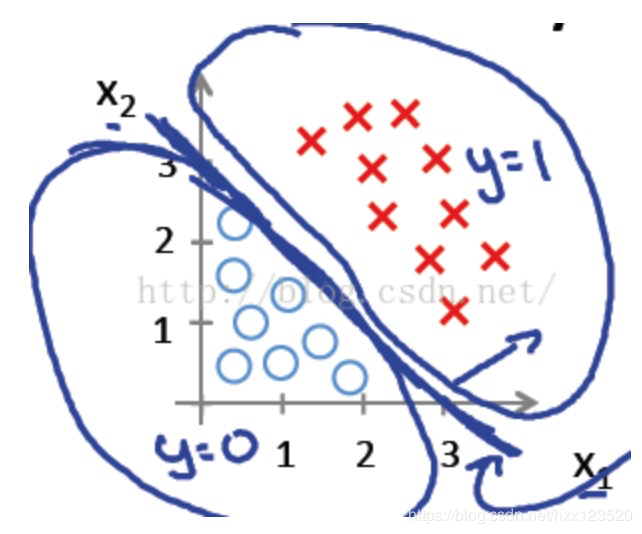
在这里插入图片描述
例1只是一个线性的决策边界，当 hθ(x)更复杂的时候，我们可以得到非线性的决策边界，例如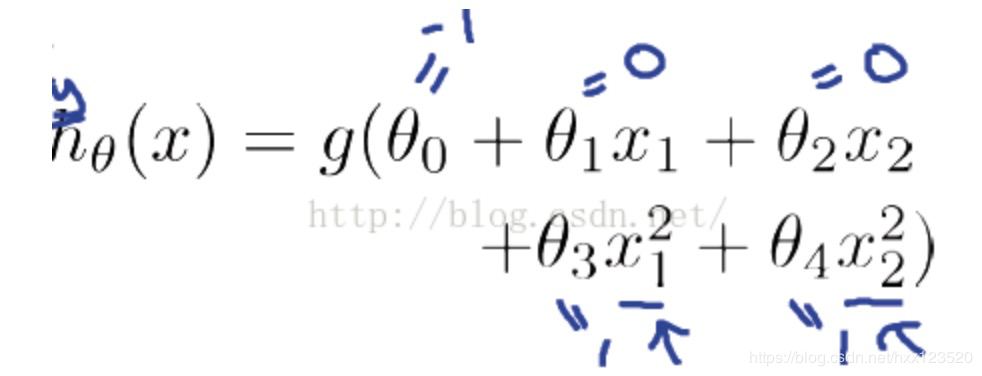：这时当−1+x12+x22⩾0-1+x_{1}^{2}+x_{2}^{2}\geqslant 0−1+x12+x22⩾0时，我们判定y=1，这时的决策边界是一个圆形，如下图所示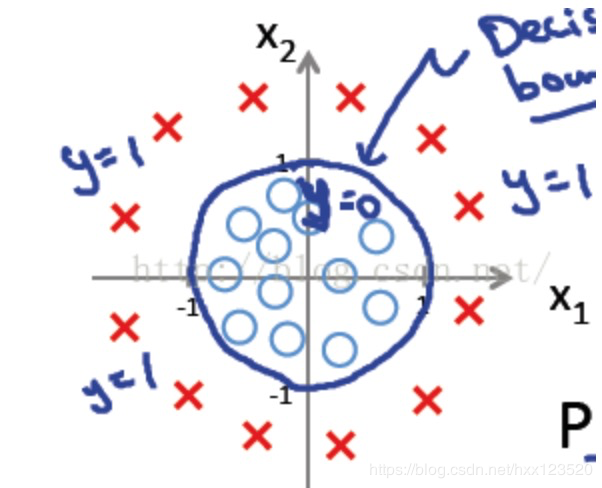：在这里插入图片描述
所以我们发现，g(θTx)g(\theta ^{T}x)g(θTx)中θTx\theta ^{T}xθTx足够复杂，在不同的情形下，能够拟合出不同的判定边界，将不同类别的样本点分离开。

4、代价函数

我们通过对判定边界的说明，知道会有合适的参数θ使得θTx=0\theta ^{T}x= 0θTx=0成为很好的分类判定边界，那么问题就来了，我们如何判定我们的参数θ是否合适，有多合适呢？更进一步，我们有没有办法去求得这样的合适参数θ呢？
这就是我们接下来提到的代价函数与梯度下降了。

在线性回归中，我们给出代价函数定义：J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
由于它是一个凸函数，所以可用梯度下降直接求解，局部最小值即全局最小值。
但在逻辑回归中，hθ(x)h_{\theta }(x)hθ(x)是一个复杂的非线性函数，属于非凸函数，直接使用梯度下降会陷入局部最小值中。类似于线性回归，逻辑回归的J(θ)J(\theta )J(θ)的具体求解过程如下：
对于输入x，分类结果为类别1和类别0的概率分别为：
P(y=1∣x;θ)=h(x);P(y=1|x;\theta )=h(x);P(y=1∣x;θ)=h(x);
P(y=0∣x;θ)=1−h(x);P(y=0|x;\theta )=1-h(x);P(y=0∣x;θ)=1−h(x);
则整合之后为：p(y∣x;θ)=(h(x))y(1−h(x))(1−y)p(y|x;\theta )=(h(x))^{y}(1-h(x))^{(1-y)}p(y∣x;θ)=(h(x))y(1−h(x))(1−y)
通过最大似然函数求损失函数 :

L(θ)=∏i=1mP(y(i)∣x(i);θ)L(\theta )=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta )L(θ)=i=1∏mP(y(i)∣x(i);θ)
L(θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)L(\theta )=\prod_{i=1}^{m}(h_{\theta }(x^{(i)}))^{y^{(i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}L(θ)=i=1∏m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)
对数似然函数为（取对数）：
l(θ)=logL(θ)l(\theta )=logL(\theta )l(θ)=logL(θ)
l(θ)=∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))l(\theta )=\sum_{i=1}^{m}(y^{(i)}logh_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))l(θ)=i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))
似然函数有极大值，此时应该使用梯度上升求最大值，但为了便于使用梯度下降法，这里将J(θ)=−1ml(θ)J(\theta )=-\frac{1}{m}l(\theta )J(θ)=−m1l(θ)
求解J(θ)J(\theta )J(θ)的最小值可以使用梯度下降法，根据梯度下降可得θ\thetaθ的更新过程为（α\alphaα为学习步长）：
θj:=θj−α∂∂θjJ(θ)\theta _{j}:=\theta _{j}-\alpha \frac{\partial }{\partial \theta _{j}}J(\theta )θj:=θj−α∂θj∂J(θ)
接下来求偏导：
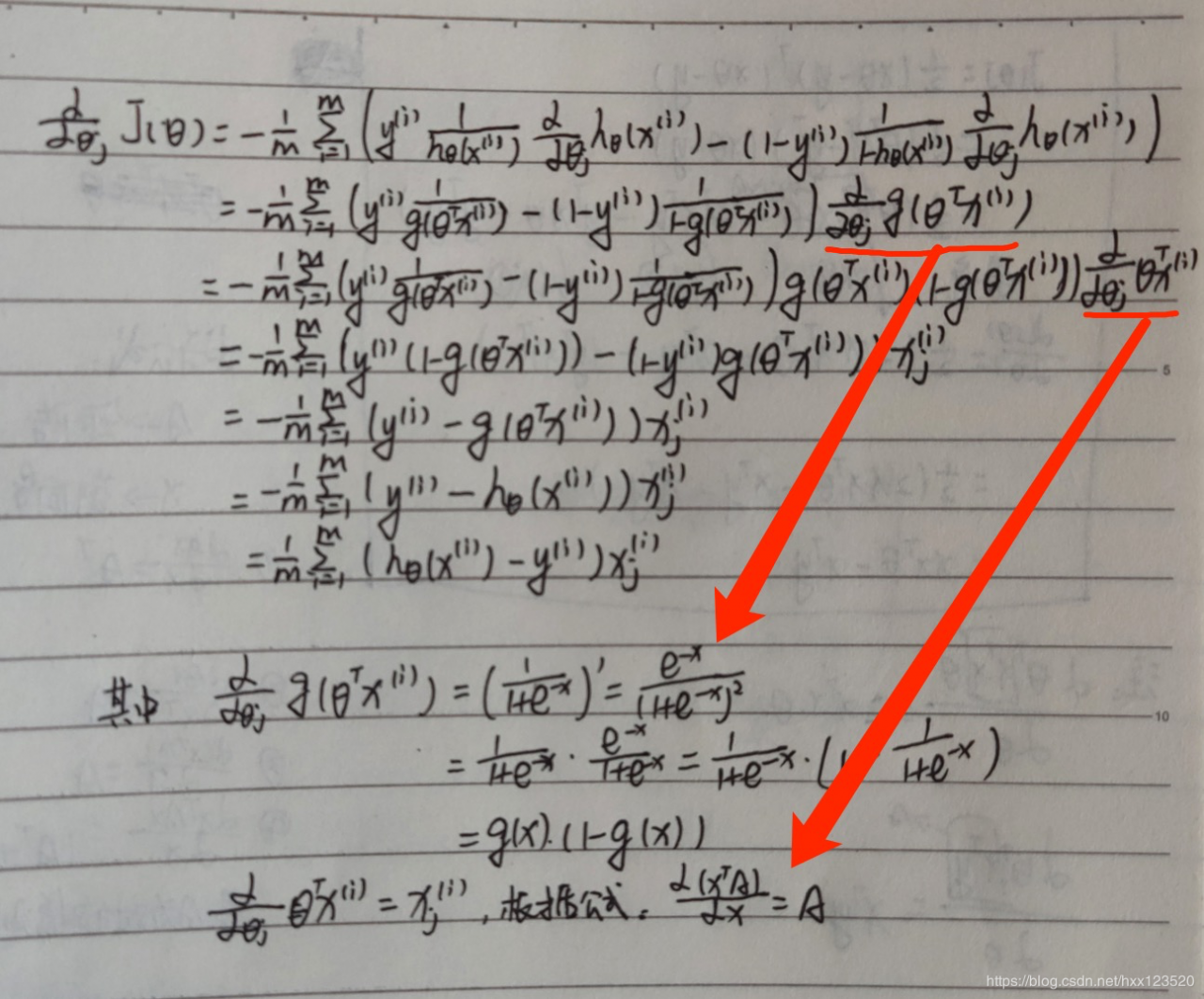在这里插入图片描述由此，θ\thetaθ 的更新过程可以写成：（下式的1m\frac{1}{m}m1 一般省略）
θj:=θj−α1m∑i=1m(hθx(i)−y(i))xj(i),(j=0...n)\theta _{j}:=\theta _{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta }x^{(i)}-y^{(i)})x_{j}^{(i)},(j=0...n)θj:=θj−αm1i=1∑m(hθx(i)−y(i))xj(i),(j=0...n)
除了梯度下降之外，还有以下优化代价函数的方法：