tensorflow 逻辑回归与交叉熵
线性回归预测的是一个连续值, 逻辑回归给出的”是”和“否”的回答

逻辑回归
sigmoid函数是一个概率分布函数, 给定某个输入,它将输出为一个概率值
多层感知器一层一层的往下映射,sigmoid->(-1,1)值
逻辑回归损失函数
1.平方差所惩罚的是与损失为同一数量级的情形
(1)mse刻画它的损失非常不恰当,因为它的概率值是在(-1,1),比如真实值是1,区分猫和狗,它的概率是1表示一条狗,而神经网络给出的结果是0.3,,这个时候如果我们用均方差来刻画它们的损失,就是1-0.3来刻画这个损失是0.7,使用平方差的损失一般是损失与原有的数据集同一个数量集的情形,假如我们的数量值取值特别的庞大,然后我们的损失值是一个很小的值,,这时候使用的平方差刻画的损失就非常的小,不利于我们的训练,训练的次数就非常非常的慢,但他不是并不能训练,它是可以用平方差训练来刻画损失的,但最好使用交叉熵
2.对于分类问题,我们最好的使用交叉熵损失函数会更有效
3.交叉熵会输出一个更大的“损失”
交叉熵损失函数
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距 离,也就是交叉熵的值越小,两个概率分布就越接近。
假设 概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交 叉熵,则:
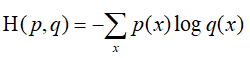
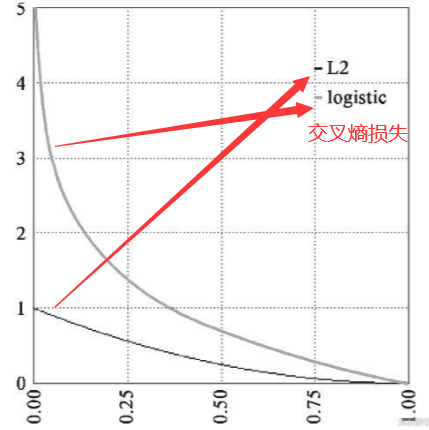
交叉熵放大了概率分布的损失
在keras里,我们使用 binary_crossentropy 来计算二元交叉熵
demo展示
import pandas as pd
# import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# 库引用时如果没有被调用,是不能成功运行程序的,可以暂时注释掉
data = pd.read_csv('./credit-a.csv', header=None) # 第一行没写参数,这样它就把第一行作为数据
data.head()
# print(data)
data.iloc[:, -1].value_counts() # 取最后一列
# print(c)
x = data.iloc[:, :-1] # iloc[]第一个参数表示取所有行,第二个参数表取最后一列之前的,这些都作为我们的数据
y = data.iloc[:, -1].replace(1, 0) # 把-1替换成0,使其只有1和0,来辨别为欺诈数据和非欺诈数据
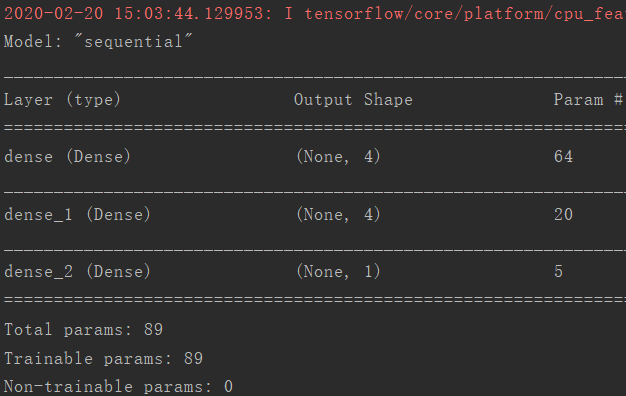
model = tf.keras.Sequential() # 顺序模型
model.add(tf.keras.layers.Dense(4, input_shape=(15,), activation='relu')) # 添加第一次隐藏层,设置4个单元数,数据的形状为前15行,然后relu激活
model.add(tf.keras.layers.Dense(4, activation='relu')) # 添加第二层隐藏层,其他的就不用填了,它会自动判断
model.add(tf.keras.layers.Dense(1, activation='sigmoid')) # 这个sigmoid他有两个隐藏层+一个输出层
model.summary()
# 编译配置
model.compile(optimizer='adam',
loss='binary_crossentropy', # 二元概率,计算交叉熵
metrics=['acc'] # 在运行过程中,计算它的正确率情况,它是个list
)
# 训练过程
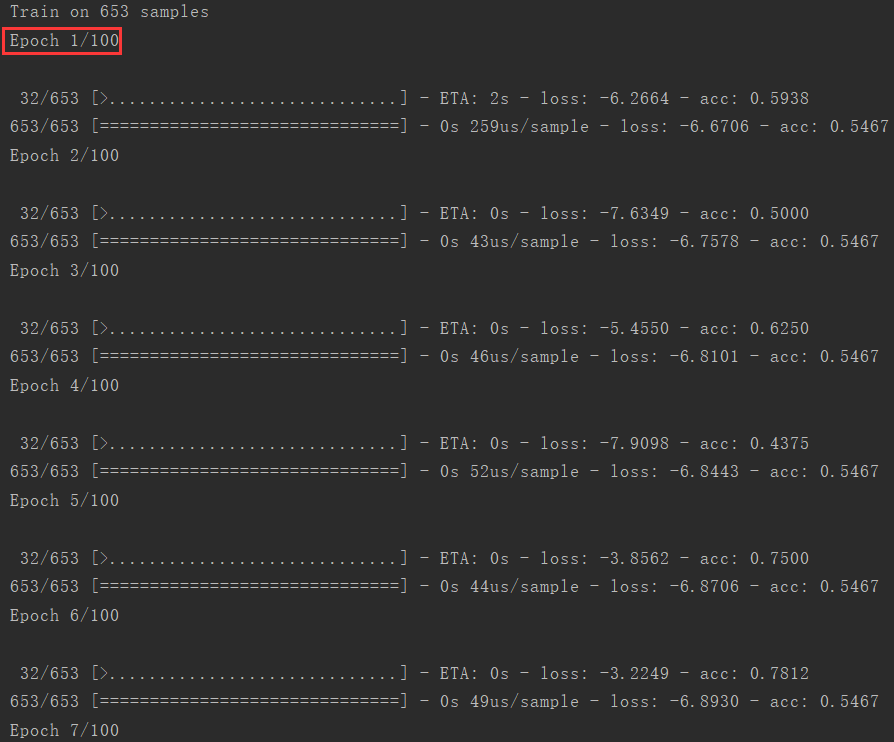
history = model.fit(x, y, epochs=100)
history.history.keys() # 字典
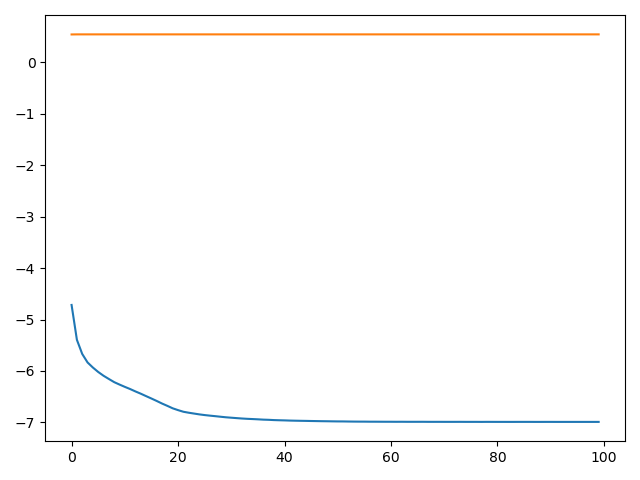
plt.plot(history.epoch, history.history.get('loss'))
plt.plot(history.epoch, history.history.get('acc'))
plt.show()
cross_entropy.py 交叉熵 参数运行结果
训练运行:
图像:
作者:Alex-panda