【leetcode系列】【算法】【简单】最小移动次数使数组元素相等(暴力法、排序、动态规划DP、数学法四方法求解)
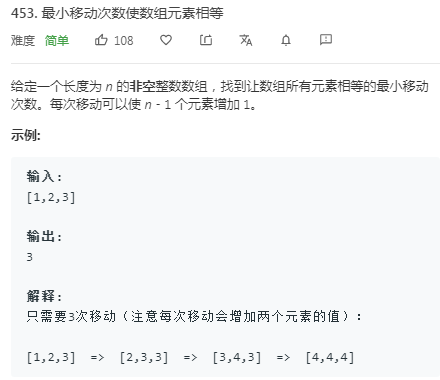
题目链接: https://leetcode-cn.com/problems/minimum-moves-to-equal-array-elements/
解题思路: 方法一:暴力法(时间O(每次都计算所有数字移动后是否全部相等,移动次数为数组中的最大元素max减去最小元素min,是本次的移动步数和对非最大值的增加值
重复此步骤,直到所有元素值相同,流程如下图所示:
假设初始数组如下:
进行第一次变更:


此时所有元素相等,均为7,停止遍历,返回结果 = 6
方法二:排序首先对数组排序,就可以在O(1)的时间内,直接找到最大和最小值,计算移动的步数
图示流程如下:
假设排序后的数组如下:

因为是排序后的数组,所以最大值为num[n - 1],最小值为num[0],根据方法一的方式,计算本次需要进行移动的步数 = num[n - 1] - num[0] = 100 - 1 = 99,以此更新所有的值,更新后如下:

本次更新后num[0]与num[n - 1]的值相同,因为移动前是排序的,所以本次移动后,最大值为num[n - 2],最小值仍然为num[0],此处添加两点额外说明:
num[0]其实和num[n - 1]其实都是最小值,只是为了所有逻辑统一,此处继续选择使用num[0] 如果移动前num[n - 2]和num[n - 1]的值相同,也不影响本次num[n - 2]是最小值,因为每次需要对n - 1个数字进行移动,所以在num[n - 1]不增加,num[n - 2]增加的情况下,num[n - 2] >= num[n - 1]的;等于的情况,是属于本来所有数字就已经一样了,导致本次移动步数是0所以据此得出,本次的移动步数 = num[n - 2] - num[0] = 198 - 100 = 98,再次修改所有值,修改后如下:

同理,此时最大值为num[n - 3],最小值为num[0]( = num[n - 1] = num[n - 2]),继续此步骤,直到遍历到num[1]为止
此外,上述的更新数字的操作,实际上是可以省去的,因为更新前后,数字的差距其实是不变的
所以可以直接计算偏移量,而不进行数字更新操作
方法三:DP先将数组进行排序,然后将问题拆解为子问题
假设当前num[i]之前(即num[0]到num[i - 1])的所有元素值已经相等,那么此时,只需要将num[0]到num[i - 1]再移动move = num[i] - num[i - 1]步,就可以使得num[0]到num[i]的所有元素值均相等
在进行此步骤的时候,会将num[i + 1]到num[n - 1]的所有元素,也同时加上move,即num[i + 1] = num[i + 1] + move
所以,在对num[i + 1]进行遍历的时候,需要先对num[i + 1]更新为num[i + 1] + move,然后再求新的move
也就是move = move + num[i + 1] - num[i],依次类推,直到遍历完成
图示如下:
假设排序后的初始数组如下:

此时先比对num[0]和num[1],move = num[1] - num[0] = 1 - 1 = 0,不对数组进行更新

然后再比对num[2]和num[1],先更新num[2] = num[2] + move = 5 + 0 = 5,然后再计算移动步数move = num[2] - num[1] = 5 - 1 = 4,更新move值:

继续遍历num[3],先更新num[3] = num[3] + move = 7 + 4 = 11:

然后本次需要新增的curr_move = num[3] - num[2] = 11 - 5 = 6,更新总move = move + curr_move = 4 + 6 = 10
继续遍历num[4],更新num[4] = num[4] + move = 9 + 10 = 19,再更新move = 10 + num[4] - num[3] = 10 + 19 - 11 = 18:

继续遍历,直到算到最后一个元素时的move,就是总移动次数
方法四:数学法转换一下思想:每次对n - 1个数字加1,就相当于每次对1个数字减一
所以问题就转换成了:把所有数字均减小为最小数字,一共需要多少步
假设min为最小值,那总的移动步数![move = \sum _{i = 0}^{n - 1}(num[i] - min)](/upload/wp-content/uploads/2020/04/ec42b0e5af94d17fcd610289e976b488-121.gif)
所以只需要找到最小值,就可以找到总的移动次数了
代码实现: 方法一:暴力法
class Solution:
def minMoves(self, nums: List[int]) -> int:
move = 0
while True:
min_idx, max_idx = 0, 0
for index, a in enumerate(nums):
if nums[min_idx] > a:
min_idx = index
if nums[max_idx] < a:
max_idx = index
if nums[min_idx] == nums[max_idx]:
break
diff = nums[max_idx] - nums[min_idx]
move += diff
for index in range(len(nums)):
if index == max_idx:
continue
nums[index] += diff
return move
方法二:排序
class Solution:
def minMoves(self, nums: List[int]) -> int:
nums.sort()
move = 0
for index in range(len(nums) - 1, 0, -1):
move += nums[index] - nums[0]
return move
方法三:动态规划DP
class Solution:
def minMoves(self, nums: List[int]) -> int:
nums.sort()
move = 0
for index in range(1, len(nums)):
nums[index] += move
move += nums[index] - nums[index - 1]
return move
方法四:数学法
class Solution:
def minMoves(self, nums: List[int]) -> int:
min_num = nums[0]
for index in range(1, len(nums)):
if nums[index] < min_num:
min_num = nums[index]
move = 0
for a in nums:
move += a - min_num
return move
作者:冰临天下