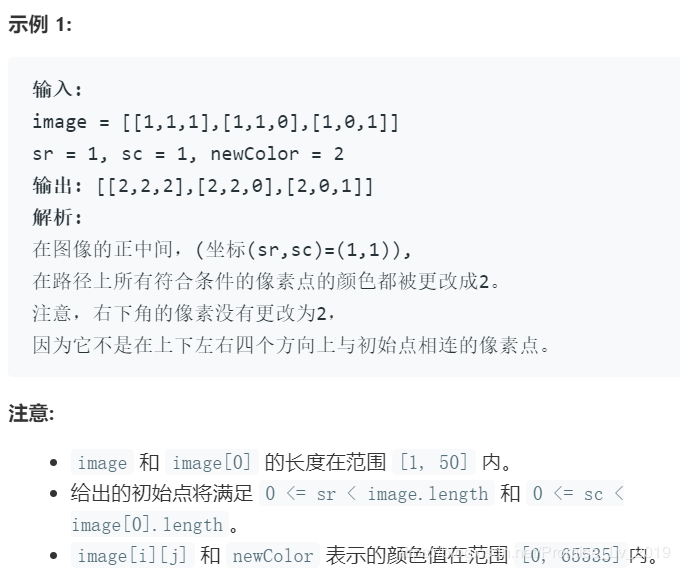
Leetcode 刷题（19）：堆栈和队列应用：图像渲染（简单版的数岛屿）

Ursula ·

更新时间:2024-11-14

· 533 次阅读

733. 图像渲染

在这里插入图片描述

难度：简单
题目分析：这道题是容易版的数岛屿（数岛屿详细解析戳这里传送门）。简单的地方在于，对于岛屿题目，我们是不清楚“1” 会出现在什么地方，所以需要构建一个双层循环，遍历矩阵每一个点；而这道题，直接给了起点，所以我们把周围一片找出来即可。

1. 解法一：递归实现的DFS

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        # 这道题简单，dfs或是bfs都可以
        # 动态规划呢？
        # 先用递归的bfs
        # sr,sc 是问题的起点，省去了一个大的遍历
        # 找到目标点，上色，相当于标记了探索过的方向
        row = len(image)
        if row == 0:
            return image
        col = len(image[0])
        old = image[sr][sc]
        if old == newColor:
            return image
        # my_stack = [(sr, sc)]
        dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))
        def dfs(image, i, j):
            for k in range(4):
                nxt_i, nxt_j = i + dirs[k][0], j + dirs[k][1]
                if nxt_i >= 0 and nxt_i = 0 and nxt_j < col:
                    if image[nxt_i][nxt_j] == old:
                        image[nxt_i][nxt_j] = newColor
                        dfs(image, nxt_i, nxt_j)
        image[sr][sc] = newColor
        dfs(image, sr, sc)
        return image

1.1 运行效果：

在这里插入图片描述

1.2 分析：

一开始运行，出现了递归超过深度？？？最后排查了有两个错误导致！

我没有先把起点的颜色给改了……于是，可能导致各种嵌套（因为没改起点的值，到达其他的点时，有可能把起点重新加入探索，中间可能会很复杂），最后造成递归超过栈的深度更新矩阵元素的时候，我把 image[nxt_i][nxt_j] 写成了 image[nxt_j][nxt_j]……

对于这二个错误，写代码的时候细心点就可以了。第一个错误则要着重强调，不管对于深度优先探索DFS还是广度优先探索DFS，经过的点，一定要先标记，这样才能避免重复的探索。

最后还有一个要强调的，题目还要考虑新标的颜色跟原来一样的情况，这种情况，意味着矩阵不用修改，直接返回就好；如果没有判断，程序依然会溢出。

2. 解法二：深度优先搜索，非递归解法

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        # 这道题简单，dfs或是bfs都可以
        # 动态规划呢？
        # 先用递归的bfs
        # sr,sc 是问题的起点，省去了一个大的遍历
        # 找到目标点，上色，相当于标记了探索过的方向
        row = len(image)
        if row == 0:
            return image
        col = len(image[0])
        old = image[sr][sc]
        if old == newColor:
            return image
        # my_stack = [(sr, sc)]
        dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))
        # 我们自己维护栈
        image[sr][sc] = newColor # 标记探索过
        my_stack = [((sr,sc), 0)] # 起点进栈,还有待探索方向
        while my_stack:
            cur, index = my_stack.pop()
            for i in range(index, 4):
                nxt = cur[0] + dirs[i][0], cur[1] + dirs[i][1] # 下一个方向
                if nxt[0]>= 0 and nxt[0] =0 and nxt[1] < col:
                    if image[nxt[0]][nxt[1]] == old:  # 下一个方向符合
                        image[nxt[0]][nxt[1]] = newColor # 标颜色
                        my_stack.append((cur, i+1))
                        my_stack.append((nxt, 0))
                        break
        return image

2.1 运行结果：

在这里插入图片描述

2.2 分析：

很奇怪，可能因为是晚上八点多提交，速度慢得可怕。但二者本质上没有区别。

这段时间做的是栈和队列的专题，写了很多使用DFS的代码，我目前受我看的教科书（裘宗燕的《数据结构与算法（Python语言描述）》）影响挺大的，比如栈每个位置保存两个信息，一个是待探索点，一个是开始方向；这其实很接近我们编写递归算法解释器函数帧存放的数据。

在教科书中，这种解法对于求解迷宫有一个非常大的好处，只要我们逐一输出栈，就能得到一条从起点到终点的路。另外一个好处，可能是每一步，待探索方向很多的时候，可以节省保存空间吧。

由于考虑到探索方向并无先后之分，下面尝试把所有方向统一入栈，然后弹出最后一个入栈方向探索。

2.3 尝试另外的DFS写法：

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        # 这道题简单，dfs或是bfs都可以
        # 动态规划呢？
        # 先用递归的bfs
        # sr,sc 是问题的起点，省去了一个大的遍历
        # 找到目标点，上色，相当于标记了探索过的方向
        row = len(image)
        if row == 0:
            return image
        col = len(image[0])
        old = image[sr][sc]
        if old == newColor:
            return image
        # my_stack = [(sr, sc)]
        dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))
		# 采用新的DFS的写法
        image[sr][sc] = newColor # 标记探索过
        my_stack = [(sr,sc)] # 起点进栈,还有待探索方向
        while my_stack:
            cur = my_stack.pop()
            for i in range(4):
                nxt = cur[0] + dirs[i][0], cur[1] + dirs[i][1] # 下一个方向
                if nxt[0]>= 0 and nxt[0] =0 and nxt[1] < col:
                    if image[nxt[0]][nxt[1]] == old:  # 下一个方向符合
                        image[nxt[0]][nxt[1]] = newColor # 标颜色
                        my_stack.append(nxt)
        return image

2.3.1 运行结果：

在这里插入图片描述

一开始速度很快，后来两次不知道怎么就又慢了……

3. 解法三：广度优先搜索 BFS

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        # 这道题简单，dfs或是bfs都可以
        # 动态规划呢？
        # 先用递归的bfs
        # sr,sc 是问题的起点，省去了一个大的遍历
        # 找到目标点，上色，相当于标记了探索过的方向
        row = len(image)
        if row == 0:
            return image
        col = len(image[0])
        old = image[sr][sc]
        if old == newColor:
            return image
        # my_stack = [(sr, sc)]
        dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))
        # 广度优先搜索，BFS,跟新的DFS很像，只是出栈的顺序不一样
        from collections import deque
        my_que = deque()
        image[sr][sc] = newColor # 标记探索过
        my_que.append((sr,sc))
        while my_que:
            cur = my_que.popleft()
            for i in range(4):
                nxt = cur[0] + dirs[i][0], cur[1] + dirs[i][1] # 下一个方向
                if nxt[0]>= 0 and nxt[0] =0 and nxt[1] < col:
                    if image[nxt[0]][nxt[1]] == old:  # 下一个方向符合
                        image[nxt[0]][nxt[1]] = newColor # 标颜色
                        my_que.append(nxt)
        return image

3.1 运行结果：

在这里插入图片描述

速度差不多，不做评论。