Python进阶:可视化学习Numpy

Natalia ·

更新时间:2024-11-13

· 974 次阅读

简介

通过可视化的方式来学习与理解Numpy中的简单概念。

文中图片出自A Visual Intro to NumPy and Data Representation

什么是Numpy？

Numpy是Python中用于数据分析、机器学习与科学计算的知名第三方库，它是Python中很多科学计算库的依赖包，如sickit-learn、SciPy、Pandas等

创建数组

Numpy中创建数组使用 np.array(list) 则可，本质其实就是将 list 转换成了 Numpy中定义的 numpy.ndarray类型，从而方便高效的进行各种矩阵运算。

In [1]: import numpy as np
In [2]: a = np.array([1,2,3])
In [3]: print(a) #数组的值
[1 2 3]
In [4]: a.dtype # 每个元素的类型
Out[4]: dtype('int64')
In [5]: a.shape #形状，　三行零列。
Out[5]: (3,)
In [6]: a.size #array的大小，其实就是array中所有元素的个数
Out[6]: 3

从代码中可以看出，我们创建了一个名为a的数组，它的形状为(3,)，即三行零列，整体大小为3，形象如下图：

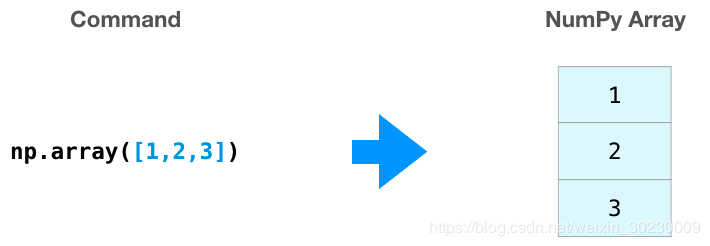
在这里插入图片描述
在通过list创建array时，如果没有指定dtype(数组元素类型)，那么就会以list中元素的类型而自动定义成对应的默认类型，如果list中全为整型，则dtype默认为int64，如果list中存在浮点型，则dtype默认为float64，当然这是可以修改的，如下：

In [7]: np.array([1,2,3]).dtype
Out[7]: dtype('int64') # list中全为整型，则dtype默认为int64
In [8]: np.array([1.0,2,3]).dtype
Out[8]: dtype('float64') # list中存在浮点型，则dtype默认为float64
In [9]: np.array([1,2,3], dtype=np.float32).dtype
Out[9]: dtype('float32') # dtype可以修改

实际使用Numpy时，通常会直接通过Numpy生成数组的初始值，而不是我们通过list去生成，Numpy为此提供了ones()、zeros()、random.random()等方法。

In [10]: n1 = np.ones(3)
In [11]: print(n1)
[1. 1. 1.]
In [12]: n1.dtype
Out[12]: dtype('float64')
In [13]: n2 = np.zeros(3)
In [14]: print(n2)
[0. 0. 0.]
In [15]: n3 = np.random.random(3)
In [16]: print(n3)
[0.95151279 0.79374927 0.52983953]

从代码可以看出，ones()方法会将数组元素全初始化为1.，zeros()与random.random()方法也都类似，需注意，这3个方法生成的数组类型都为float64，形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0N3BIq1j-1582164696562)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821103023.png)]

数组运算

创建两个数组，将他们相加，获得一个新的数组。

In [20]: data = np.array([1,2])
In [21]: ones = np.ones(2)
In [22]: data + ones
Out[22]: array([2., 3.])

可以发现，我们不用使用for迭代的方式去运算数组结构，直接通过+操作符就完事了，抽象做的非常好，如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wuunH5Gk-1582164696563)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821104941.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NWgzul0q-1582164696564)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821104951.png)]

与加法类似，减法、乘法、除法如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X2Smkruk-1582164696565)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821105103.png)]

加减乘除法除了数组之间可以使用，数组与单纯的数字也可以计算

In [23]: data
Out[23]: array([1, 2])
In [24]: data + 1
Out[24]: array([2, 3])
In [25]: data - 3
Out[25]: array([-2, -1])
In [26]: data /6
Out[26]: array([0.16666667, 0.33333333])
In [27]: data * 1.6
Out[27]: array([1.6, 3.2])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zGZl8cyS-1582164696566)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821105508.png)]

数组的索引

我们可以通过下标或切片的方式去获得数组中对应的值

In [30]: data = np.array([1,2,3])
In [31]: data[0]
Out[31]: 1
In [32]: data[1]
Out[32]: 2
In [33]: data[0:2]
Out[33]: array([1, 2])
In [34]: data[1:]
Out[34]: array([2, 3])

从上述代码可以看出，对一维数组的操作其实与对list的操作是一样的

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ymky5Ep3-1582164696566)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821105609.png)]

数组的聚合

数组除了简单运算外，还提供了很多方法方便我们快速获取数组中存放数据的一些特征，简单使用如下：

In [34]: data = np.array([1,2,3])
In [35]: data.max() # 获取数组的最大值
Out[35]: 3
In [36]: data.min() # 获取数组的最大值
Out[36]: 1
In [37]: data.sum() # 获取数组中元素的和
Out[37]: 6 # 1+2+3
In [38]: data.mean() # 获取数组的平均值
Out[38]: 2.0 # (1+2+3)/3
In [39]: data.prod() # 获取数组中所有元素相乘的值
Out[39]: 6 # 1*2*3
In [40]: data.std() # 获取数组中所有元素的标准差
Out[40]: 0.816496580927726 # np.sqrt( ((1-2)^2 + (2-2)^2 + (3-2)^2)/3 )

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2iUnSoxY-1582164696567)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821110355.png)]

创建矩阵

上面的讨论都基于一维数组，但Numpy其实可以运算任意维度的数组，接着就来讨论矩阵(二维数组)的使用

创建数组同样简单，如下

In [43]: np.array([[1,2], [3,4]])
Out[43]:
array([[1, 2],
       [3, 4]])

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xRarYdd7-1582164696569)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821110632.png)]

如果需要Numpy自己初始化数据，依旧可以使用ones()等方法，如下图

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7eYcAhFj-1582164696570)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821110647.png)]

ones()等方法需要传入一个元组，元组的第一个元素表示行数，第二个元素表示列数，同理类推，创建更高维度的数组，如下创建三维数组

In [45]: np.ones((3,2,2))
Out[45]:
array([[[1., 1.],
        [1., 1.]],
       [[1., 1.],
        [1., 1.]],
       [[1., 1.],
        [1., 1.]]])

矩阵运算

矩阵运算与一维数组运算类似，如果两个矩阵大小相同，那么进行加减乘除时，Numpy会按照矩阵中对应的位置逐步进行加减乘除运算，代码如下：

In [46]: data = np.array([[1,2],[3,4]])
In [47]: ones = np.ones((2,2))
In [48]: data + ones
Out[48]:
array([[2., 3.],
       [4., 5.]])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5ATwYIHk-1582164696570)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821111126.png)]

Numpy无法对不同大小的矩阵进行运算，会出现相应的报错，如下：

In [55]: data = np.array([1,2,3])
In [56]: powers_of_ten = np.array([[1,10], [100, 1000], [10000, 100000]])
In [57]: data * powers_of_ten
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
 in 
----> 1 data * powers_of_ten
ValueError: operands could not be broadcast together with shapes (3,) (3,2)

但可以让矩阵与一维数组进行运算

In [49]: ones_row = np.ones(2)
In [50]: ones_row
Out[50]: array([1., 1.])
In [52]: data = np.array([[1,2], [3,4], [5,6]])
In [53]: data + ones_row
Out[53]:
array([[2., 3.],
       [4., 5.],
       [6., 7.]])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AGsaFjqY-1582164696571)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821141843.png)]

矩阵点积

与矩阵相乘容易混淆的就是矩阵的点积，在Numpy中利用dot()方法实现矩阵的点积运算，代码如下：

In [55]: data = np.array([1,2,3])
In [56]: powers_of_ten = np.array([[1,10], [100, 1000], [10000, 100000]])
In [57]: data.dot(powers_of_ten)
Out[57]: array([ 30201, 302010])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-adGaqu64-1582164696571)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821142053.png)]

两个矩阵要实现点积，第一矩阵的列数要等于第二个矩阵的行数，如上图中，data的列数为3，而powers_of_ten矩阵的行数也为3，此时进行点积就会获得一个(1,2)形状的矩阵，其中的具体的运算规则如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vN0aXAqg-1582164696572)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821142353.png)]

data中的每一行与powers_of_ten中的每一列中的元素两两相乘，得到的结果再相加，从而获得最终的结果，如果data有多行，则进行多次这样的操作。

矩阵的索引

与一维数组的索引类似，简单使用一下矩阵索引

In [59]: data = np.array([[1,2],[3,4],[5,6]])
In [60]: data[0,1] # 0 表示第一行，1 表示第二列
Out[60]: 2
In [61]: data[1:3] # 1:3 表示第二行到第四行，切片是左闭右开的
Out[61]:
array([[3, 4],
       [5, 6]])
In [62]: data[0:2, 0]
Out[62]: array([1, 3])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GIdmQxZL-1582164696572)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821142824.png)]

矩阵聚合

与一维数组类似，Numpy同样可以对矩阵进行各种操作

In [63]: data
Out[63]:
array([[1, 2],
       [3, 4],
       [5, 6]])
In [64]: data.max() # 矩阵中最大值
Out[64]: 6
In [65]: data.min() # 矩阵中最小值
Out[65]: 1
In [66]: data.sum() # 矩阵的总和
Out[66]: 21
In [67]: data.prod() # 矩阵中所有元素相乘的值
Out[67]: 720 # 1*2*3*4*5*6
In [68]: data.std() # 标准差
Out[68]: 1.707825127659933

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TNi0l7DR-1582164696573)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821143117.png)]

但对于多维数组而言(不只是矩阵)可以使用axis参数跨纬度进行聚合操作。

这里先尝试使用axis对矩阵中的行或列进行聚合

In [82]: data
Out[82]:
array([[1, 2],
       [3, 4],
       [5, 6]])
In [83]: data.max(axis=0)
Out[83]: array([5, 6])
In [84]: data.max(axis=1)
Out[84]: array([2, 4, 6])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q1ZN34xd-1582164696574)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821143854.png)]

更高维度的数组也是类似的使用方式，如下：

In [77]: data2 = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
In [78]: data2.shape
Out[78]: (2, 2, 3)
In [79]: data2
Out[79]:
array([[[ 1,  2,  3],
        [ 4,  5,  6]],
       [[ 7,  8,  9],
        [10, 11, 12]]])
In [80]: data2.max(axis=2)
Out[80]:
array([[ 3,  6],
       [ 9, 12]])
In [81]: data2.max(axis=2).max(axis=0)
Out[81]: array([ 9, 12])
In [82]: data2.max(axis=2).max(axis=1)
Out[82]: array([ 6, 12])

转置与重塑

转置是处理矩阵的常见需求，它类似于沿着矩阵的对角线反转了一下矩阵，效果如下：

In [86]: data
Out[86]:
array([[1, 2],
       [3, 4],
       [5, 6]])
In [87]: data.T # 转置
Out[87]:
array([[1, 3, 5],
       [2, 4, 6]])

形象如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mjNV6bNP-1582164696574)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821144139.png)]

而某些时候，我们想重塑整个数组的形状，如将一维数组重塑为二维的矩阵，如下：

In [88]: data = np.array([1,2,3,4,5,6])
In [89]: data.reshape(2,3) #将一维数组重塑成形状为 (2,3) 的矩阵
Out[89]:
array([[1, 2, 3],
       [4, 5, 6]])
In [90]: data.reshape(3,2)
Out[90]:
array([[1, 2],
       [3, 4],
       [5, 6]])

形象如下图，需要注意，重塑后的数组其元素个数要与重塑前数组的元素个数相同。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-USwoixdP-1582164696575)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821144318.png)]

更多的维度

Numpy可以创建任意维度的数组，这也是它的中心数据结构被称为ndarray(n维数组)的原因。

创建方式类似，注意list的个数则可，每一维对应着一个list

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f1UvAsZb-1582164696575)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821144625.png)]

ones()等方法使用方式也类似，要创建多少维，就传入对应长度的元组

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FbrPx9sf-1582164696576)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821144934.png)]

需要注意的是，如果我们打印高维数组，为了方便理解，这里以三维为例，如果我们打印三维数组，其打印的顺序与上面可视化显示的顺序是不同的，Numpy会将最后一维优先打印出了，如下：

In [91]: np.ones((4,3,2))
Out[91]:
# 打印最后一维的2个元素，然后才是第二维的3个元素，最后才是第一维的4个元素
array([[[1., 1.], 
        [1., 1.],
        [1., 1.]],
       [[1., 1.],
        [1., 1.],
        [1., 1.]],
       [[1., 1.],
        [1., 1.],
        [1., 1.]],
       [[1., 1.],
        [1., 1.],
        [1., 1.]]])

结尾

Numpy的简单使用就介绍完了，更多复杂的使用方式交个后面的文章来介绍吧，记得关注HackPython，拜拜。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NqqLfGuN-1582164696577)(https://raw.githubusercontent.com/ayuLiao/images/master/20190821150724.png)]

作者：懒编程-二两

化学 NumPy 可视化 Python

1024 个赞