卡尔曼滤波与状态估计例题python实现

Jayne ·

更新时间:2024-09-21

· 600 次阅读

卡尔曼滤波与状态估计例题python实现

关于卡尔曼滤波的原理这里就不赘述了，很多大佬说的很棒，这里就把网课上看到的例题在这里做一下
巩固一下

卡尔曼滤波的两个步骤 预测更新（Predict):
预测状态量：
x^=(t∣t−1)=A~x(t−1)+Bu(t)\hat x=(t|t-1)=\widetilde{A}x(t-1)+Bu(t)x^=(t∣t−1)=Ax(t−1)+Bu(t)
预测误差协方差矩阵：
P(t∣t−1)=AP(t−1)AT+QP(t|t-1)=AP(t-1)A^T+QP(t∣t−1)=AP(t−1)AT+Q 测量更新（Correct）:
最优估计状态量：
x~(t)=x^(t∣t−1)+K(t)[z(t)−Hx^(t∣t−1)]\widetilde{x}(t)=\hat x(t|t-1)+K(t)[z(t)-H\hat x(t|t-1)]x(t)=x^(t∣t−1)+K(t)[z(t)−Hx^(t∣t−1)]
计算误差增益：
K(t)=P(t∣t−1)HT[R+HP(t∣t−1)HT]K(t)=\frac{P(t|t-1)H^T}{[R+HP(t|t-1)H^T]}K(t)=[R+HP(t∣t−1)HT]P(t∣t−1)HT
误差协方差矩阵：
P(t)=[I−K(t)H]P(t∣t−1)P(t)=[I-K(t)H]P(t|t-1)P(t)=[I−K(t)H]P(t∣t−1) 状态方程和观测方程

状态方程：
x(t)=Ax(t−1)+Bu(t)+w(t)x(t)=Ax(t-1)+Bu(t)+w(t)x(t)=Ax(t−1)+Bu(t)+w(t)
观测方程：
z(t)=Hx(t)+v(t)z(t)=Hx(t)+v(t)z(t)=Hx(t)+v(t)

问题

假设一辆小车在做匀加速运动，初速度为0，加速度为5（m/s2）5（m/s^2）5（m/s2），小车上装有速度传感器，采样频率为10Hz10Hz10Hz ，传感器测量误差为高斯白噪声。尝试对小车的运动速度进行估计。

设k时刻时的速度为xkx_kxk，则系统的状态方程为：
xk=xk−1+5×110+wk−1x_k=x_{k-1}+5\times \frac{1}{10}+w_{k-1}xk=xk−1+5×101+wk−1
测量方程为：
zk=xk+vkz_k=x_k+v_kzk=xk+vk

www 和 vvv 分别是系统和测量误差
初始参数设定，根据状态方程和观测方程，不难得出初始参数：

	#初始参数设定
	A=np.array([1])
	B=np.array([1])
	U=0.5
	H=np.array([1])

由于传感器每一步的采样频率的 0.1 秒，这里设步数是500步

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
#预测更新的方程
def predict_update(A,B,U,P0,Q,X0):
    Xp=A*X0+B*U
    Pp=A*P0*A.T+Q
    return Xp,Pp
#测量更新的方程 
def correct_update(H,R,Pp,Z,Xp):
    #print(Xp)
    Xp=np.array([Xp])
    I=np.eye(Xp.shape[0])  
    K=(Pp*H.T)/(H*Pp*H.T+R)    
    Xup=Xp+K*(Z-H*Xp)
    Pup=(I-K*H)*Pp
    return Xup,Pup
def main():
    #初始参数设定 
    A=np.array([1])
    B=np.array([1])
    U=0.5
    H=np.array([1])
    step=500
    #设置观测值 
    v=np.random.normal(0,10,step) #设置一个均值为0，方差为10的1x500的高斯噪声 
    true_x=0.5*np.arange(0,step) #假设没有噪声时的速度 
    temp=true_x+v #真实的速度就是加上噪声
    X_0=np.zeros(step)  #先验概率初始值 
    #print(X_0.shape)
    #print(X_0)
    X0=np.zeros((step))  #后验概率初始值 
    Z=np.zeros((step))  #观测值初始值 
    Z=temp  #加上噪声的车辆测量速度，用于模拟观测值 
    P0=np.array([1])  #后验估计的协方差初值
    Q=np.array([10])  #状态方程噪声协方差矩阵
    R=np.array([10])  #测量方程协方差矩阵
    for i in range(2,step):
        X_0[i],P_0=predict_update(A,B,U,P0,Q,X0[i-1])
        X0[i],P0=correct_update(H,R,P_0,Z[i],X_0[i])
    #print(P0.shape)
    plt.figure(figsize=(16,10))
    plt.plot(np.arange(500),Z,'y',label="观测值") #黄色代表观测值
    plt.plot(np.arange(500),true_x,'r',label="真实值")#红色代表真实值 
    plt.plot(np.arange(500),X0,'b',label="卡尔曼滤波")#蓝色代表卡尔曼滤波 
    plt.legend(loc='best')
    plt.show()
if __name__=='__main__':
    main()

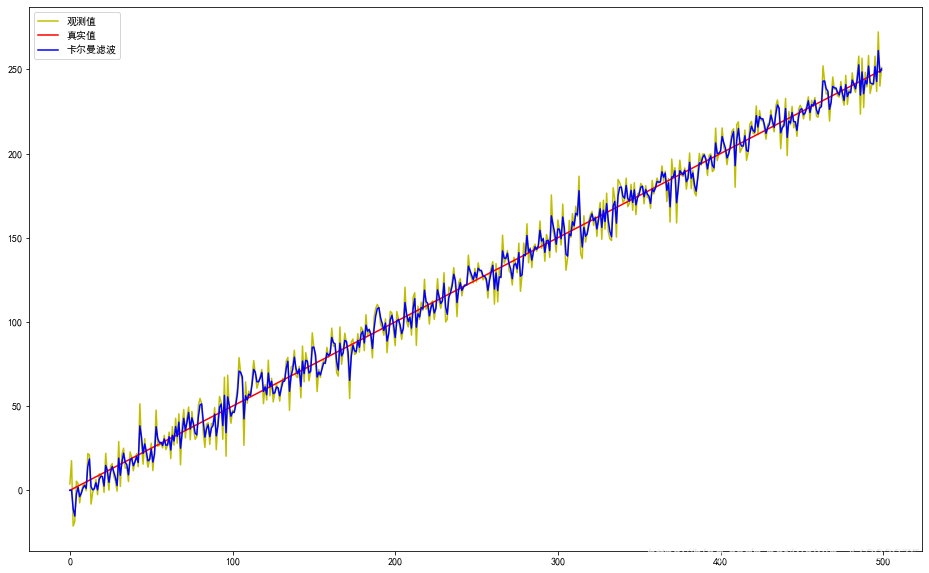
在这里插入图片描述
上图可以看出，观测值比真实值偏差较大，而滤波值实现了很好的估计。