机器学习中的决策边界绘制

本文将会直接给出代码，主要目的在于对代码进行解释，熟悉使用python的Numpy和matplotlib库绘制决策边界曲线，代码来自于https://blog.csdn.net/dengjiaxing0321/article/details/70545740。
代码如下

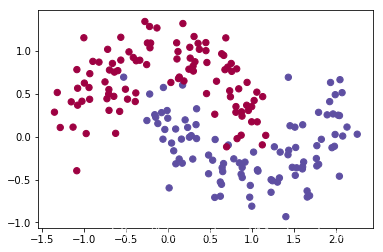
import numpy as np from sklearn.datasets import make_moons import matplotlib.pyplot as plt np.random.seed(0) X, y = make_moons(200, noise=0.20) plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral) plt.show() 输入数据集X具有两个特征，y是类别输出标签（0|1），plt.scatter方法将X中第一列（第一个特征）和第二列（特征2）作为横纵坐标进行散点图绘制； s=40，表示散点的大小为40，可以输入与样本数量相同的列表，表示不同点的不同大小； c=y，c表示颜色，可以使用c='b’这样的命令将所有散点表示为同一颜色，也可以是一个与样本数量相同的序列，因为y中的取值有两个（0或1），散点根据y的索引表示为两种不同的颜色用以区分不用类别； cmap表示Colormap实体或者是一个colormap的名字，cmap =
plt.cm.Spectral实现的功能是给label为1的点一种颜色，给label为0的点另一种颜色。

def plot_decision_boundary(pred_func): x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5 y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5 h = 0.01 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # 用预测函数预测一下 Z = pred_func(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) # 然后画出图 plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral) plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral) 定义x_min, x_max， y_min, y_max 表示设定两个特征对应的横纵坐标的最大值和最小值，同时通过+.5附加一点边缘填充； 使用np.meshgrid()方法通过网格点的横纵坐标向量生成坐标矩阵，如下所示，上述示例中输入的横坐标向量为np.arange(x_min, x_max, h), 纵坐标向量为np.arange(y_min, y_max, h)； x = np.array([0, 1, 2]) y = np.array([0, 1]) X, Y = np.meshgrid(x, y) print(X) print(Y) [[0 1 2] [0 1 2]] [[0 0 0] [1 1 1]] np.c_[xx.ravel(), yy.ravel()],xx.ravel(),其中xx.ravel()表示将多维数组降为一维返回视图（view），即对降维后的数据做修改会影响原始矩阵（xx.flatten()对降维后的数据做修改会不影响原始矩阵），随后使用np.c_[]方法按列叠加两个矩阵，也可以说是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等； plt.contourf（）方法用于绘制等高线，xx和yy表示输入坐标矩阵，Z表示通过输入参数得到输出的函数（或结果） plt.cm.Spectral用以给不同类别填充不同颜色； from sklearn.linear_model import LogisticRegressionCV clf = LogisticRegressionCV() clf.fit(X, y) # 绘制决策边界 plot_decision_boundary(lambda x: clf.predict(x)) plt.title("Logistic Regression") plt.show()

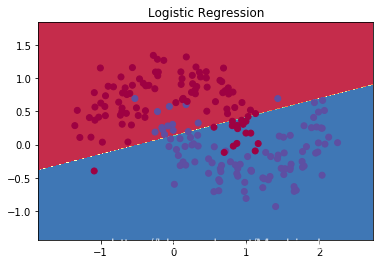
使用sklearn库中的逻辑回归模型对数据进行分类预测，调用绘制决策边界函数plot_decision_boundary，输入为预测函数，lambda x: clf.predict(x)表示输入为x，输出为clf.predict(x)的函数,lambda argument_list: expression表示创建了一个以argument_list为输入，以expression为表达式的函数，实例如下；

add=lambda x, y: x+y add add(1,2) 3
作者：June �

决策 边界 学习 决策边界 机器学习