TensorFlow2.0(十)--实现深度可分离卷积神经网络

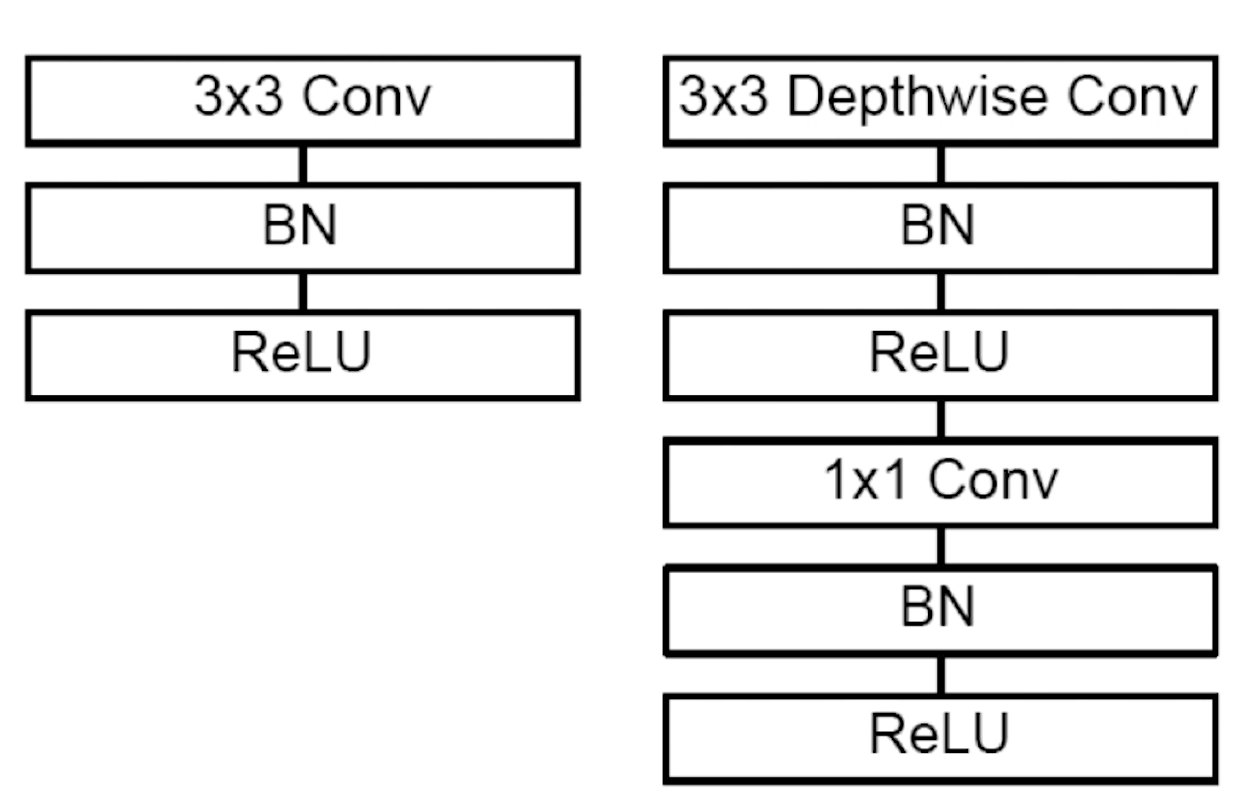
深度可分离卷积神经网络1. 深度可分离卷积网络介绍1. 1 深度可分离卷积网络与普通卷积网络1.2 普通卷积与深度可分离卷积计算量对比2. 深度可分离卷积网络实现2.1 导入相应的库2.2 数据集的加载与处理2.3 构建模型2.4 2.4 模型的编译与训练2.5 学习曲线绘制2.6 模型验证 1. 深度可分离卷积网络介绍 1. 1 深度可分离卷积网络与普通卷积网络

深度可分离卷积神经网络是卷积神经网络的一个变种，可以对卷积神经网络进行替代。对于普通的卷积申请网络，如下图左边部分所示，由卷积层，批归一化操作与激活函数构成的。对于深度可分离卷积网络，它是由一个3x3深度可分离的卷积层，批归一化，激活函数，1x1普通卷积层，批归一化，激活函数构成。在卷积神经网络中，将下图左边部分替换为右边部门，那么卷积神经网络就成为了深度可分离卷积网络。

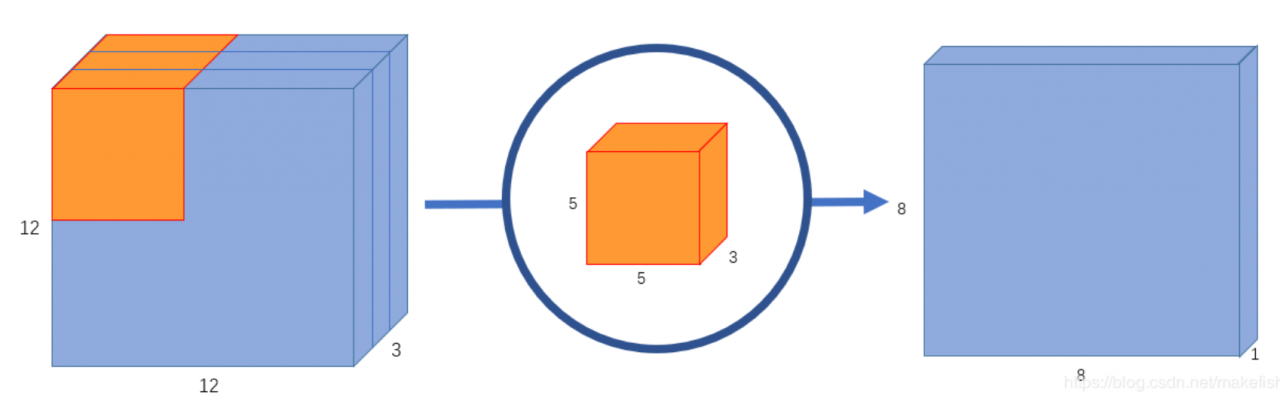
对于普通的卷积神经网络，输出通道是和所有的输入通道有关的。在深度可分离卷积网络里，输出通道只与单个输入通道有关。其他博主（摘自深度可分离卷积）有个图对比的很明显，这里借用一下：

正常卷积
原始图像是二维的，大小是12x12。由于是RGB格式的，所以有三个通道，这相当于是一个3维的图片。其输入图片格式是：12x12x3。滤波器窗口大小是5x5x3。这样的话，得到的输出图像大小是8x8x1。

这仅仅提取到的图片里面的一个属性。如果希望获取图片更多的属性，譬如要提取256个属性，则：
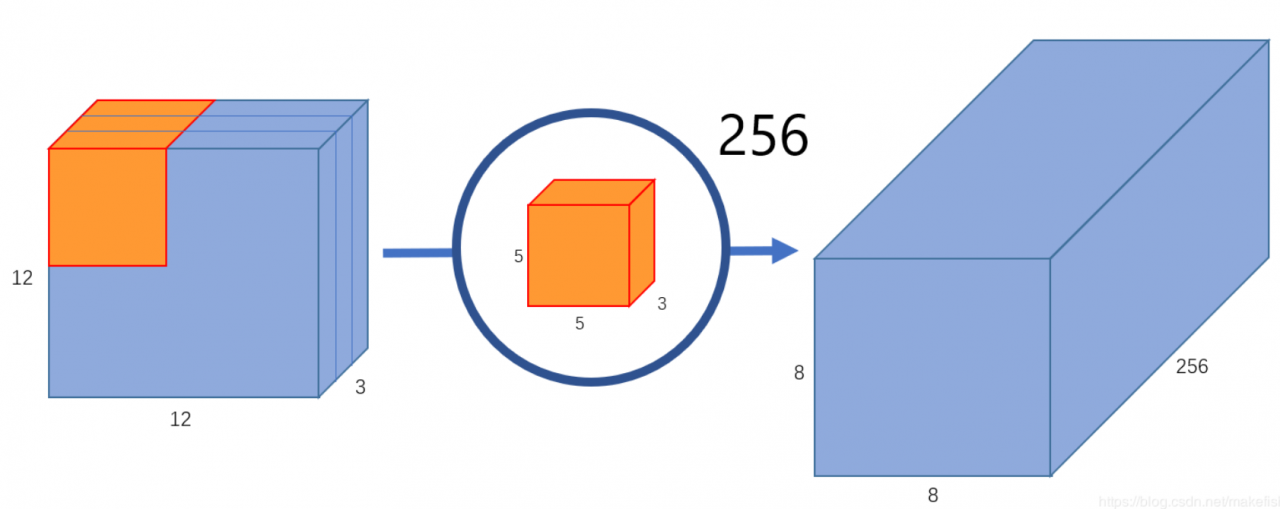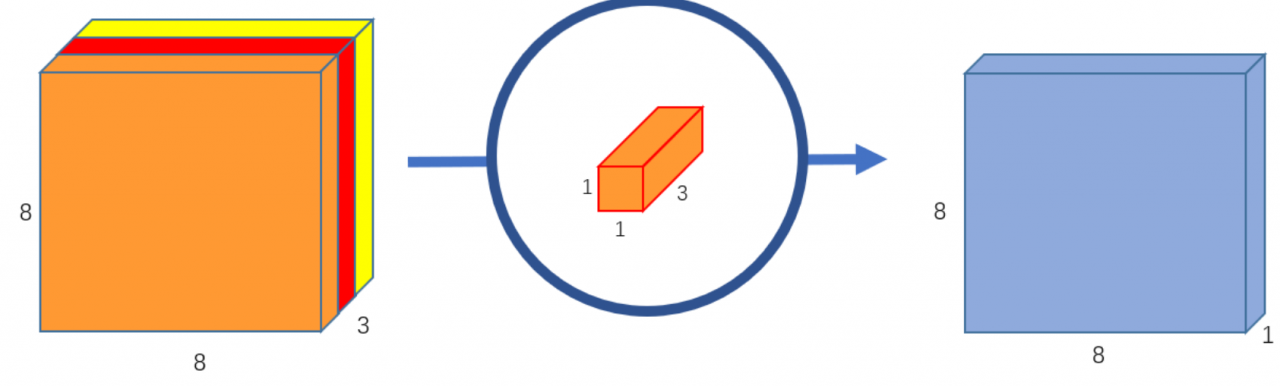
深刻可分离卷积
深度可分离卷积的方法有所不同。正常卷积核是对3个通道同时做卷积。也就是说，3个通道，在一次卷积后，输出一个数。深度可分离卷积分为两步，第一步是用三个卷积对三个通道分别做卷积，这样在一次卷积后，输出3个通道的属性值
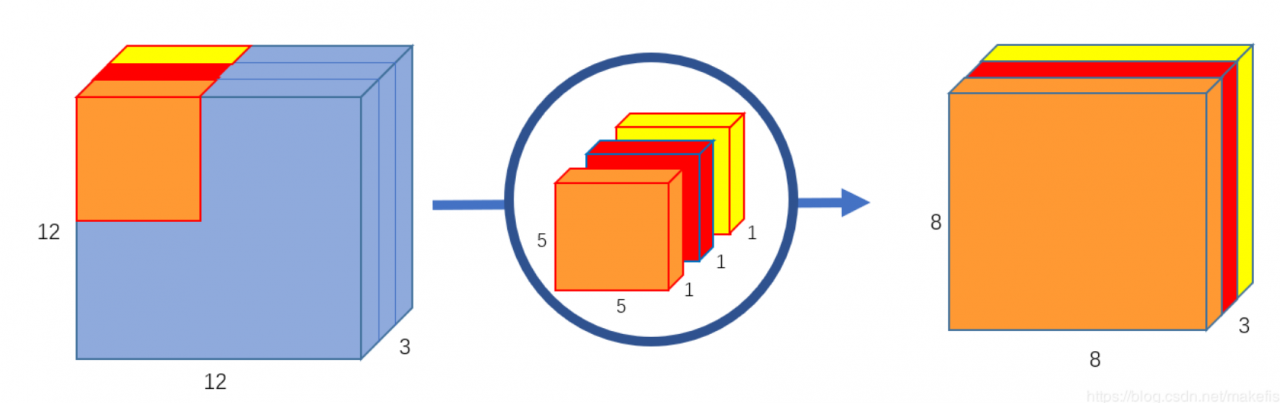
第二步是用卷积核1x1x3对三个通道再次做卷积，这个时候的输出就和正常卷积一样，是8x8x1：

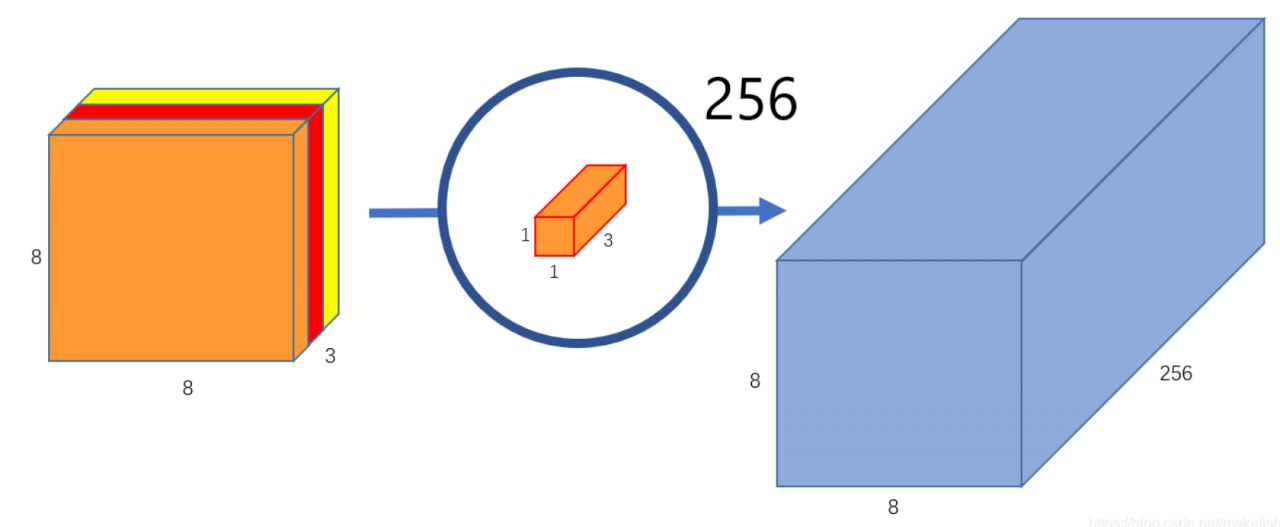
如果要提取更多的属性，则需要设计更多的1x1x3卷积核心就可以：

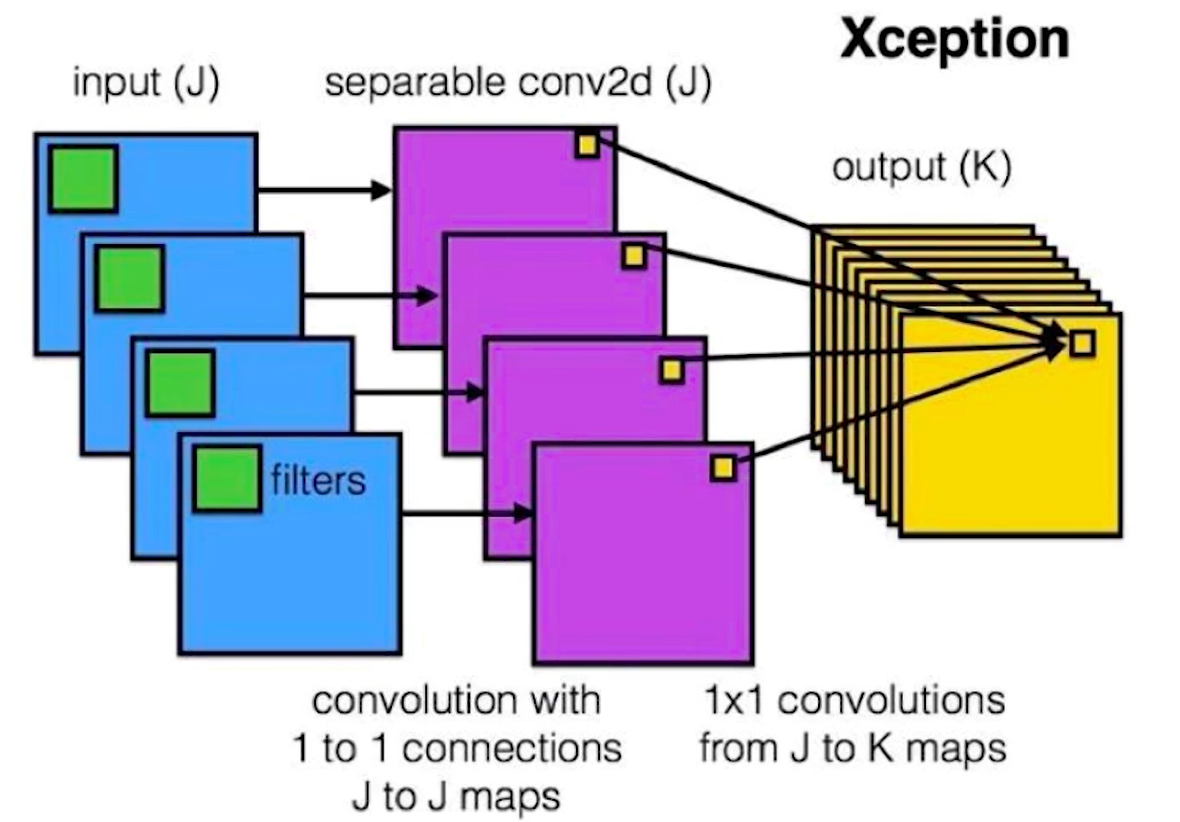
因为深度可分离神经网络的输出通道至于单个输入通道有关，所以很大程度上降低了参数计算量。
1.2 普通卷积与深度可分离卷积计算量对比 普通卷积计算量
普通卷积的计算量公式如下所示：

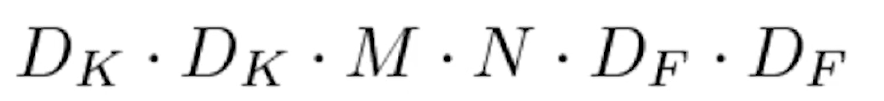
其中Dk代表卷积核的边长（一般都用正方形的卷积核），Df代表输入图像的边长（一般输入图像会被处理为正方形像素的图像），M代表输入通道数，N是输出通道数。对于普通卷积，因为乘法的计算量远远大于加法，所以公式中忽略了加法的计算量，只考虑乘法。 深度可卷积计算量
深度可卷积的计算量公式有两个，第一个是深度可分离的计算量：

其中参数的含义与普通卷积一样。
第二个公式是1x1卷积的计算公式：

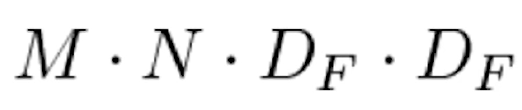
其中参数的含义与普通卷积一样。 深度可分离卷积的优化比例

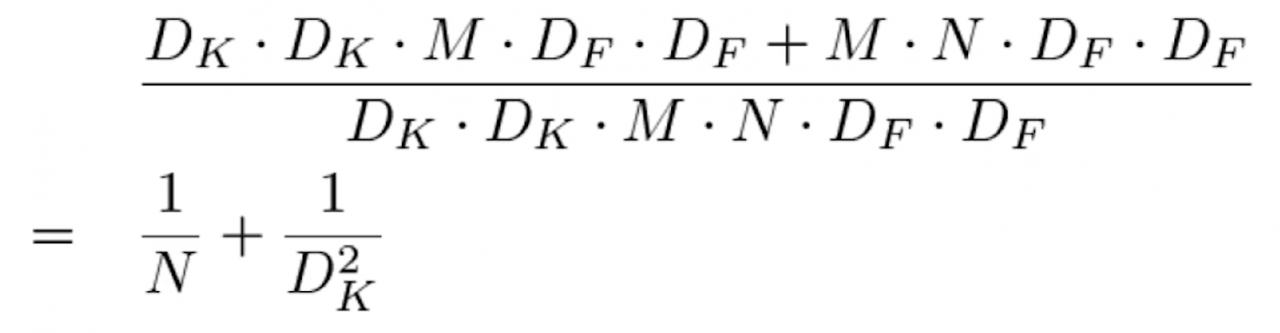
假设输出通道数N为96个，卷积核的边长为3，那么深度可分离卷积的计算量优化比例能够达到1/9左右。所以深度可分离卷积网络可以部署在移动端上使用。 2. 深度可分离卷积网络实现

本文利用TF2.0框架中的tf.keras来实现一个深度可分离卷积网络，数据集采用之前CNN使用的fashion_mnist 的数据集，里面是像素为28*28的黑白图像。

2.1 导入相应的库

首先我们要导入要用到的python库

# matplotlib 用于绘图 import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline # 处理数据的库 import numpy as np import sklearn import pandas as pd # 系统库 import os import sys import time # TensorFlow的库 import tensorflow as tf from tensorflow import keras 2.2 数据集的加载与处理

加载数据集：

# 下载数据集 fashion_mnist = keras.datasets.fashion_mnist # 拆分训练集与测试集 (x_train_all, y_train_all),(x_test, y_test) = fashion_mnist.load_data() # 对训练集进行拆分，前5000个数据集作为验证集，其余的作为数据集 x_valid, x_train = x_train_all[:5000], x_train_all[5000:] y_valid, y_train = y_train_all[:5000], y_train_all[5000:]

数据归一化可以减少模型的过拟合现象，从而可以提高模型的分类准确率，这里我们使用sklearn中的Standardscaler库对数据进行归一化处理：

from sklearn.preprocessing import StandardScaler # 初始化scaler对象 scaler = StandardScaler() # x_train: [None, 28, 28] -> [None, 784] # 因为数据是int型，但是归一化要做除法，所以先转化为float32型 # 训练集数据使用的是 fit_transform，和验证集与测试集中使用的 transform 是不一样的 # fit_transform 可以计算数据的均值和方差并记录下来 # 验证集和测试集用到的均值和方差都是训练集数据的，所以二者的归一化使用 transform 即可 # 归一化只针对输入数据， 标签不变 x_train_scaled = scaler.fit_transform( x_train.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28, 1) x_valid_scaled = scaler.transform( x_valid.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28, 1) x_test_scaled = scaler.transform( x_test.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28, 1) 2.3 构建模型

模型利用keras自带的keras.layers.SeparableConv2D来实现，模型的结构与TensorFlow2.0(九)–Keras实现基础卷积神经网络中的结构一样，只是用深度可分离卷积代替了普通卷积：

# tf.keras.models.Sequential()用于将各个层连接起来 model = keras.models.Sequential() # 第一层卷积层 model.add(keras.layers.SeparableConv2D(filters = 32, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu', # 激活函数relu input_shape = (28, 28, 1))) # 输入维度是1通道的28*28 # 第二层卷积层 model.add(keras.layers.SeparableConv2D(filters = 32, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu')) # 激活函数relu # 最大池化层 model.add(keras.layers.MaxPool2D(pool_size=2)) # 第三层卷积层 model.add(keras.layers.SeparableConv2D(filters = 64, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu')) # 激活函数relu # 第四层卷积层 model.add(keras.layers.SeparableConv2D(filters = 64, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu')) # 激活函数relu # 最大池化层 model.add(keras.layers.MaxPool2D(pool_size = 2)) # 第五层卷积层 model.add(keras.layers.SeparableConv2D(filters=128, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu')) # 激活函数relu # 第六层卷积层 model.add(keras.layers.SeparableConv2D(filters=128, # 卷积核数量 kernel_size = 3, # 卷积核尺寸 padding = 'same', # padding补齐，让卷积之前与之后的大小相同 activation = 'relu')) # 激活函数relu # 最大池化层 model.add(keras.layers.MaxPool2D(pool_size = 2)) # 全连接层 model.add(keras.layers.Flatten()) # 展平输出 model.add(keras.layers.Dense(128, activation = 'relu')) model.add(keras.layers.Dense(10, activation = "softmax")) # 输出为 10的全连接层

我们看看模型的结构：

model.summary()

通过与TensorFlow2.0(九)–Keras实现基础卷积神经网络对比可以发现，相同的网络结构下，普通卷积神经网络的参数数量为435306个，而替换为深度可分离卷积之后参数数量变为183987个，而且其中147584个参数来自于全连接层。可以发先深度可分离卷积极大地减少了参数的数量。

2.4 2.4 模型的编译与训练

我们来看一下网络的效果如何：

model.compile(loss = "sparse_categorical_crossentropy", # 稀疏分类交叉熵损失函数 optimizer = keras.optimizers.SGD(0.01), # 优化函数为随机梯度下降 ，学习率为0.01 metrics = ["accuracy"]) # 优化指标为准确度

开始训练：

history = model.fit(x_train_scaled, y_train, # 训练数据 epochs = 10, # 训练周期，数据分为10次进行训练 validation_data = (x_valid_scaled, y_valid),) # 验证集

训练过程为：

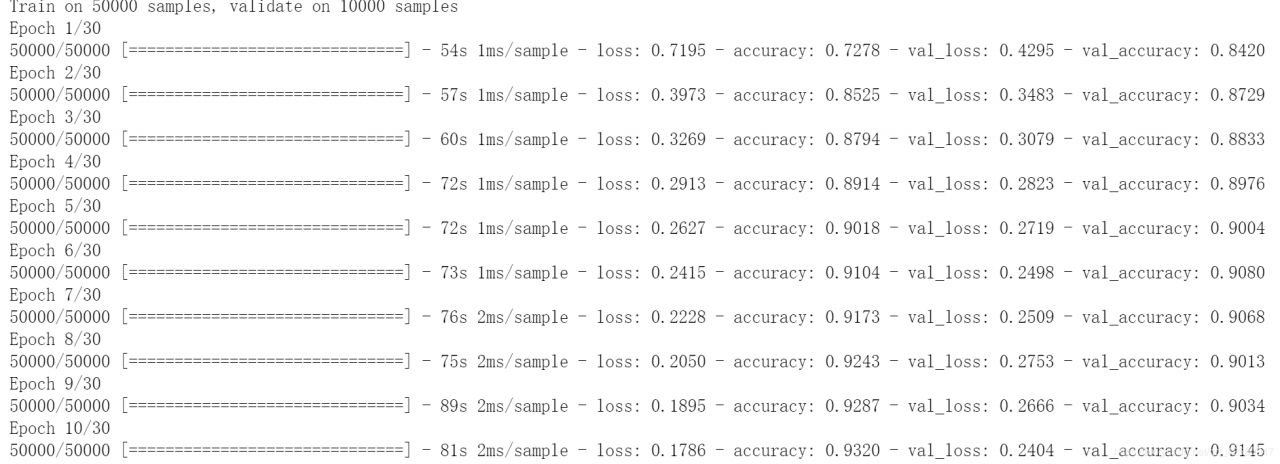
2.5 学习曲线绘制 def plot_learning_curves(history): pd.DataFrame(history.history).plot(figsize=(8, 5)) plt.grid(True) plt.gca().set_ylim(0, 1) plt.show() plot_learning_curves(history)

2.6 模型验证

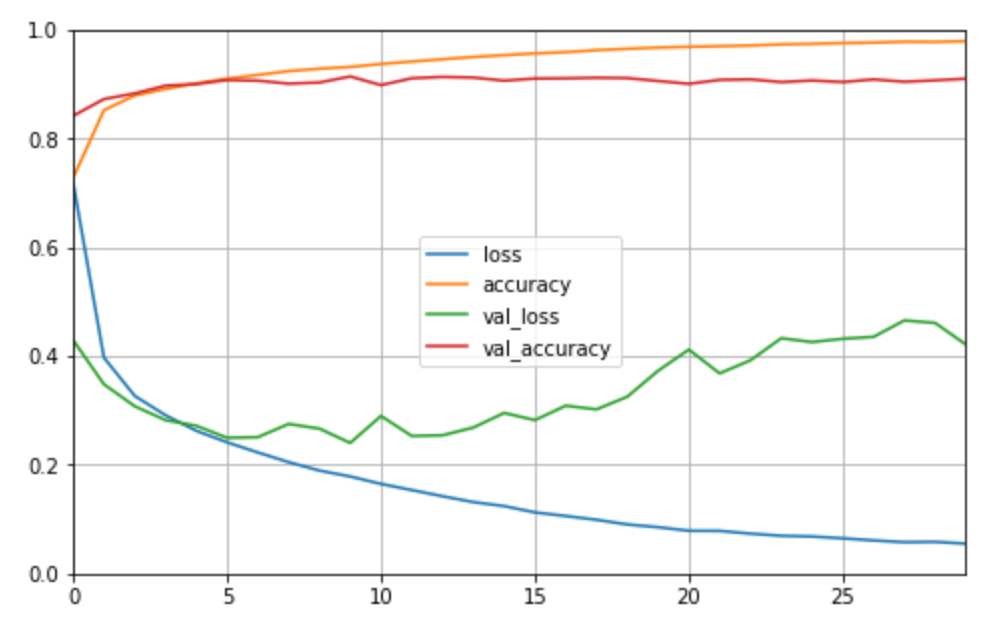
我们在验证集上看看模型的表现：

model.evaluate(x_test_scaled, y_test, verbose = 0)

输出结果为：

我们训练了十次的CNN在验证集上能够达到90.91%的准确率，相比于普通的卷积网络参数量下降的同时，准确率提升了一点。可能的原因为这次训练了30次，而且更改了优化函数为Adam。

作者：爱吃骨头的猫、

卷积神经网络 tensorflow 神经网络 卷积