基于站点数据的图卷积神经网络的实现 pyotrch

基于站点数据的图卷积神经网络的实现 pyotrch问题描述数据的预处理 问题描述

基于简单数据的图卷积神经网络展示，假设有5个空间相关的点（nodes），每个点有一个特征（feature），通过图卷积利用5个点的数据对某一点数据进行订正。
参考多篇博客和github代码基于python编译了图卷积神经网络，主要使用pytorch实现图卷积，具体是否正确还请各位大佬多多指教。

数据的预处理 数据预处理
研究中基于点的距离建立了***adjacency matrix***，代码如下 lon_lat = np.array([[32.0464,101.831],[32.0725,101.841],[32.0756,101.712],[32.1031,101.631],[31.94,101.148]]) #利用geodesic计算地球表面距离 a = np.ones((5,5)) for i in range(0,5): for j in range(0,5): a[i,j] = geodesic(lon_lat[i,:], lon_lat[j,:]).km #以15km为界限，建立adjacency matrix a[np.where(a15)] = 0 a = a-np.eye(5,5) 计算Degree Matrix
计算Degree Matrix代码使用https://github.com/johncava/GCN-pytorch.git 所提供代码 def preprocess(A): # Get size of the adjacency matrix size = len(A) # Get the degrees for each node degrees = [] for node_adjaceny in A: num = 0 for node in node_adjaceny: if node == 1.0: num = num + 1 # Add an extra for the "self loop" num = num + 1 degrees.append(num) # Create diagonal matrix D from the degrees of the nodes D = np.diag(degrees) # Cholesky decomposition of D D = np.linalg.cholesky(D) # Inverse of the Cholesky decomposition of D D = np.linalg.inv(D) # Create an identity matrix of size x size I = np.eye(size) # Turn adjacency matrix into a numpy matrix A = np.matrix(A) # Create A hat A_hat = A + I # Return A_hat return A_hat, D 神经网络的搭建
基于pytorch搭建图卷积神经网络，卷积过程代码参考https://github.com/johncava/GCN-pytorch.git #Pytorch 搭建神经网络标准开头 class GCN_net(nn.Module): def __init__(self,A,D): super(GCN_net, self).__init__() self.tn_fc0 = nn.Linear(5,5) self.tp = nn.Linear(5,1) #基于adj matrix 和 Degree matrix 计算 Laplacian matrix def DA_cal(self,x,A,D): [row,col] = x.shape A = [A]*row A = np.array(A) D = [D]*row D = np.array(D) A = torch.from_numpy(A) A = A.float() A = Variable(A, requires_grad=False) D = torch.from_numpy(D) D = D.float() D = Variable(D, requires_grad=False) DA = torch.matmul(D, A) DA = torch.matmul(DA, D) return DA #图卷积函数，卷积过程在三维矩阵上进行， #最后结果reshape为二维矩阵 def DA_cov(self, x,A,D): [row,col] = x.shape DA = self.DA_cal(x,A,D) x = x.reshape(row,5,1) x = torch.matmul(DA,x) x = x.reshape(row,5) return x #基于图卷积的前向转播 def forward(self, x,A,D): x = self.DA_cov(x,A,D) x = F.tanh(self.tn_fc0(x)) x = self.DA_cov(x,A,D) x = self.tp(x) return x 神经网络训练参数设置
pytorch三板斧之一，设置学习率，batch size ，epoch，训练算法等，在图卷积中需要确定的参数仅为每一层之间的weight matrix EPOCH = 100 BATCH_SIZE = 64 LR = 0.005 net = GCN_net(A,D) optimizer = torch.optim.Adam(net.parameters(), lr = LR, weight_decay=0) loss_function = nn.MSELoss() 神经网络训练
pytorch第三板斧，打完收工 records = [] loss_list = [] v_loss_list = [] for epoch in range(EPOCH): losses = [] for step,(x,y) in enumerate(train_loader): b_x = Variable(x.view(-1, 5)) b_y = Variable(y.view(-1, 1)) net.train() outputs = net(b_x,A,D) optimizer.zero_grad() loss = loss_function(outputs, b_y) loss.backward() # 误差反向传播, 计算参数更新值 optimizer.step() # 将参数更新值施加到 net 的 parameters 上 if step % 50 == 0: val_loss = [] net.eval() for step,(vx,vy) in enumerate(vaild_loader): v_x = Variable(vx.view(-1, 5)) v_y = Variable(vy.view(-1, 1)) v_out = net(v_x,A,D) v_loss = loss_function(v_out, v_y) val_loss.append(v_loss) print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| vaild loss: %.4f' % v_loss.data.numpy()) loss_list.append(loss.data.numpy()) v_loss_list.append(v_loss.data.numpy()) 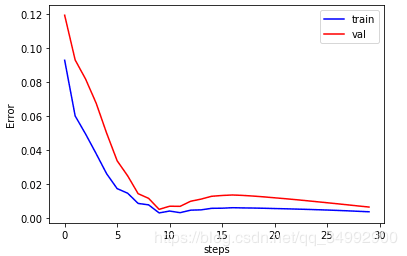plt.figure(26) plt.plot(loss_list,color = 'blue') plt.plot(v_loss_list, color = 'red') plt.xlabel('steps') plt.ylabel('Error')

5. 问题与请教
安装参考文献和参考的代码简单编写的图卷积神经网络，其实编写成功后很心虚，代码的准确性尚待探究，还请各位大佬多多指教，有什么问题还请不吝赐教。
对于图神经网络的理论，我也是一知半解，如果有什么好的学习资料，还请大家多多分享啊！

[1]: Kipf, Thomas N., and Max Welling. “Semi-supervised classification with graph convolutional networks.” arXiv preprint arXiv:1609.02907 (2016).
[2]: https://github.com/johncava/GCN-pytorch.git

作者：orient2019

数据 卷积神经网络 神经网络 卷积