Pytorch学习笔记——卷积神经网络基础
卷积神经网络包含卷积层、池化层
1、卷积层 二维互相关运算输入的二维矩阵与一个二维核矩阵的二维互相关计算,通常情况下核矩阵size小于输入矩阵,举例
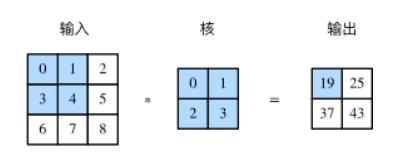
这里实现为0×0+1×1+3×2+4×3=19,然后核矩阵在输入矩阵中向右移动一格,再算1×0+2×1+4×2+5×3=25,以此类推
import torch
import torch.nn as nn
# corr2d函数实现二维互相关运算,输入矩阵X,核矩阵K,返回输出矩阵Y
def corr2d(X, K):
H, W = X.shape
h, w = K.shape
Y = torch.zeros(H - h + 1, W - w + 1) # (H-h)/1 + 1 , w
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum() #矩阵对应相乘相加
return Y
二维卷积层
是输入矩阵与核矩阵的互相关运算加上标量偏置,卷积层用到的并非卷积运算而是互相关运算
# 继承nn.Module父类
class Conv2D(nn.Module):
# Conv2D(kernel_size)
def __init__(self, kernel_size):
super(Conv2D, self).__init__()
self.weight = nn.Parameter(torch.randn(kernel_size))
self.bias = nn.Parameter(torch.randn(1))
# forward(x)
def forward(self, x):
return corr2d(x, self.weight) + self.bias # 二维互相关运算加偏差,广播机制
举例
学习卷积核以检测颜色边缘
X = torch.ones(6, 8)
Y = torch.zeros(6, 7)
X[:, 2: 6] = 0
Y[:, 1] = 1
Y[:, 5] = -1
print(X) # size(6,8)
print(Y) # size(6,7) 列数比特征少一列,0为左到右一列数据不变,1为减1,-1为0减-1,检测图像颜色边缘
conv2d = Conv2D(kernel_size=(1, 2)) # 核size
step = 30
lr = 0.01
for i in range(step):
# 求Y_hat
Y_hat = conv2d(X) # forward(X)
l = ((Y_hat - Y) ** 2).sum()
# l从y_hat反向传播
l.backward()
# 梯度下降
conv2d.weight.data -= lr * conv2d.weight.grad
conv2d.bias.data -= lr * conv2d.bias.grad
# 梯度清零
conv2d.weight.grad.zero_()
conv2d.bias.grad.zero_()
if (i + 1) % 5 == 0:
print('Step %d, loss %.3f' % (i + 1, l.item()))
print(conv2d.weight.data)
print(conv2d.bias.data)
2、特征图与感受野
特征图:二维卷积层输出的矩阵被称为输入矩阵某一级别的特征,且特征随着卷积层数量增加而愈发抽象
感受野:输入阴影部分为输出阴影部分的感受野,输入3x3矩阵为输出2x2矩阵的感受野
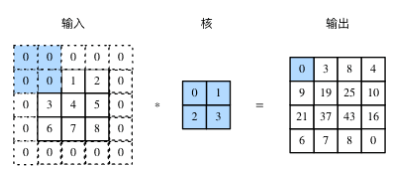
填充:通常填0,在上下,或者左右填充数字以改变数据矩阵形状
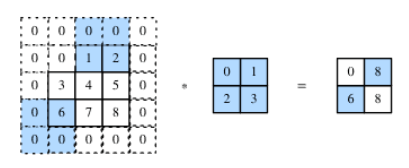
步幅:卷积核在输入数组每次滑动的行数列数,如下为行步幅为2,列步幅为3
通常情况下,我们可以通过控制填充与步幅的关系来控制输出矩阵形状
![]()
其中n,p,k,s分别为行列方向上的输入、填充、核和步幅
如RGB图像中输入通道数为3,多输入通道中每一个通道对应一个卷积核,分别做二维互相关运算然后相加得到输出矩阵,可以得知输入size为ci×h×w,卷积核size为ci×kh×kw,输出size与单输入通道与单核做二维互相关计算一致
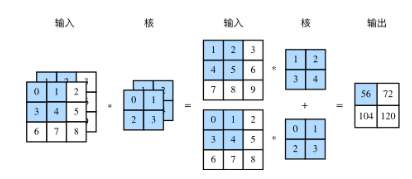
多输出通道模型如下
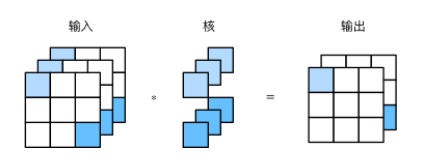
若输入层为ci×h×w,输出通道为co,则卷积核size为co×ci×kh×kw,单输出层size与单输入层与单卷积核做二维互相关运算一致
可以在不改变高和宽的情况下改变通道数
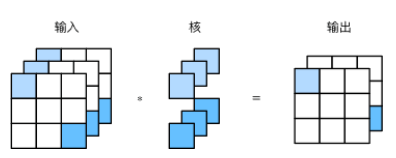
我们在卷积神经网络中使用奇数高宽的核,比如 3×3 , 5×5 的卷积核,对于高度(或宽度)为大小为 2k+1 的核,令步幅为1,在高(或宽)两侧选择大小为 k 的填充,便可保持输入与输出尺寸相同
Pytorch实现卷积层
# 卷积层的实现利用了nn.Conv2d
# 4train_nums, 2 channels, 3 high, 5 wide
X = torch.rand(4, 2, 3, 5)
print(X.shape)
# padding(1, 2) 意思是行(上下)分别增加一行0,列(左右)分别增加一列0
# 卷积层结构参数输入通道数等于X通道数,Kernel size整体小于等于X的size
conv2d = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(3, 5), stride=1, padding=(1, 2))
Y = conv2d(X)
print('Y.shape: ', Y.shape)
print('weight.shape: ', conv2d.weight.shape)
print('bias.shape: ', conv2d.bias.shape)
5、池化层
分成均值池化与最大池化,以最大池化举例,二维互相关操作以感受野内最大值代替,同理均值以感受野内均值代替
池化层之后不做矩阵相加操作,也就是说输入数据经过池化后通道数不改变
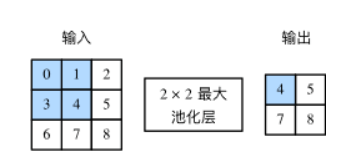
Pytorch实现
# 主要运用了nn.MaxPool2d函数
# 均值池化 nn.AvgPool2d
X = torch.arange(32, dtype=torch.float32).view(1, 2, 4, 4) #(1,2,4,4)尺寸,值为1-32的四维矩阵
pool2d = nn.MaxPool2d(kernel_size=3, padding=1, stride=(2, 1))
Y = pool2d(X)
print(X)
print(Y)
笔记内容来自动手学深度学习Pytorch版
作者:DanzerWoo