《动手学深度学习》Task04 ：卷积神经网络基础；leNet；卷积神经网络进阶

Ipo ·

更新时间:2024-11-11

· 953 次阅读

Task04 ：卷积神经网络基础；leNet；卷积神经网络进阶 1.卷积神经网络基础

下面是一些卷积神经网络的基本概念：

二维互相关运算
二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。

在这里插入图片描述

import torch 
import torch.nn as nn
def corr2d(X, K):
    H, W = X.shape
    h, w = K.shape
    Y = torch.zeros(H - h + 1, W - w + 1)
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = torch.tensor([[0, 1], [2, 3]])
Y = corr2d(X, K)
print(Y)
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

互相关运算与卷积运算

卷积层得名于卷积运算，但卷积层中用到的并非卷积运算而是互相关运算。我们将核数组上下翻转、左右翻转，再与输入数组做互相关运算，这一过程就是卷积运算。由于卷积层的核数组是可学习的，所以使用互相关运算与使用卷积运算并无本质区别。

特征图与感受野

填充

步幅

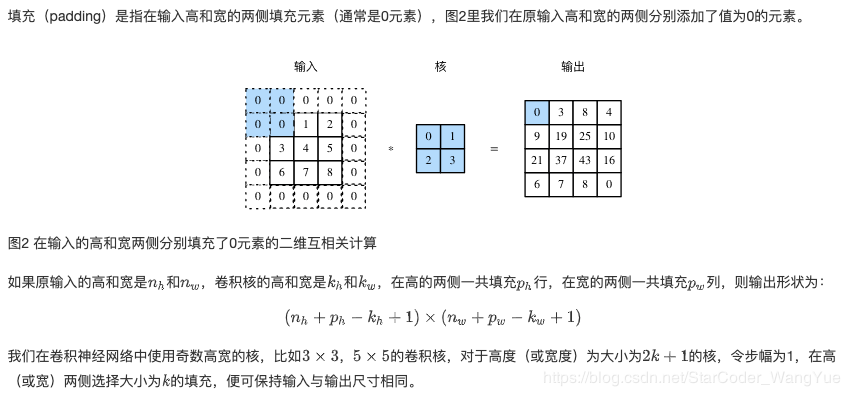在这里插入图片描述

多输入通道和多输出通道
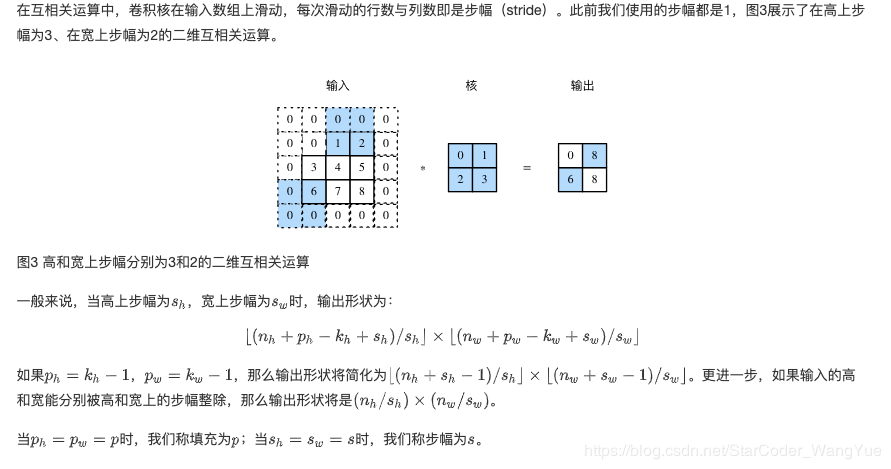
在这里插入图片描述

多输入通道

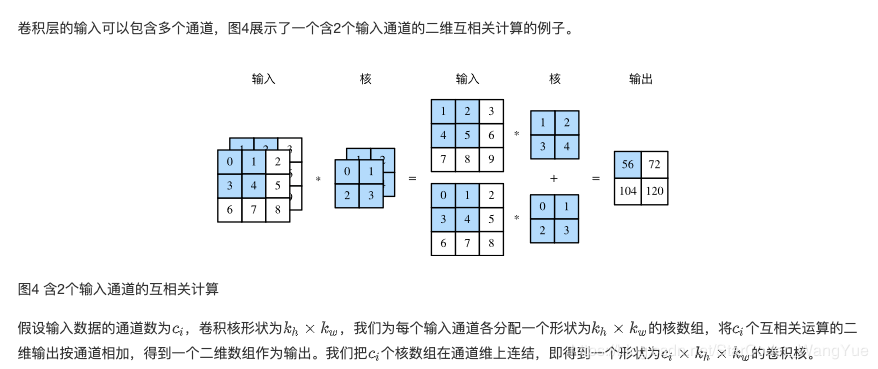
在这里插入图片描述

多输出通道

在这里插入图片描述

卷积层与全连接层的对比

在这里插入图片描述

卷积层的简洁实现

X = torch.rand(4, 2, 3, 5)
print(X.shape)
conv2d = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(3, 5), stride=1, padding=(1, 2))
Y = conv2d(X)
print('Y.shape: ', Y.shape)
print('weight.shape: ', conv2d.weight.shape)
print('bias.shape: ', conv2d.bias.shape)

池化二维池化层
池化层主要用于缓解卷积层对位置的过度敏感性。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。图6展示了池化窗口形状为2×2的最大池化。
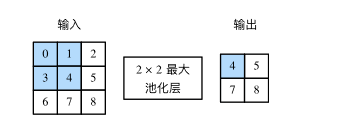
在这里插入图片描述

池化层的简洁实现：

X = torch.arange(32, dtype=torch.float32).view(1, 2, 4, 4)
pool2d = nn.MaxPool2d(kernel_size=3, padding=1, stride=(2, 1))
Y = pool2d(X)
print(X)
print(Y)

2.LeNet

Convolutional Neural Networks
使用全连接层的局限性：

图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。对于大尺寸的输入图像，使用全连接层容易导致模型过大。

使用卷积层的优势：

卷积层保留输入形状。卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

LeNet分为卷积层块和全连接层块两个部分。下面我们分别介绍这两个模块。
在这里插入图片描述

#import
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
import torch
import torch.nn as nn
import torch.optim as optim
import time
class Flatten(torch.nn.Module):  #展平操作
    def forward(self, x):
        return x.view(x.shape[0], -1)
class Reshape(torch.nn.Module): #将图像大小重定型
    def forward(self, x):
        return x.view(-1,1,28,28)      #(B x C x H x W)
net = torch.nn.Sequential(     #Lelet                                                  
    Reshape(),
    nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), #b*1*28*28  =>b*6*28*28
    nn.Sigmoid(),                                                       
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*6*28*28  =>b*6*14*14
    nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),           #b*6*14*14  =>b*16*10*10
    nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),                              #b*16*10*10  => b*16*5*5
    Flatten(),                                                          #b*16*5*5   => b*400
    nn.Linear(in_features=16*5*5, out_features=120),
    nn.Sigmoid(),
    nn.Linear(120, 84),
    nn.Sigmoid(),
    nn.Linear(84, 10)
)
#print
X = torch.randn(size=(1,1,28,28), dtype = torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

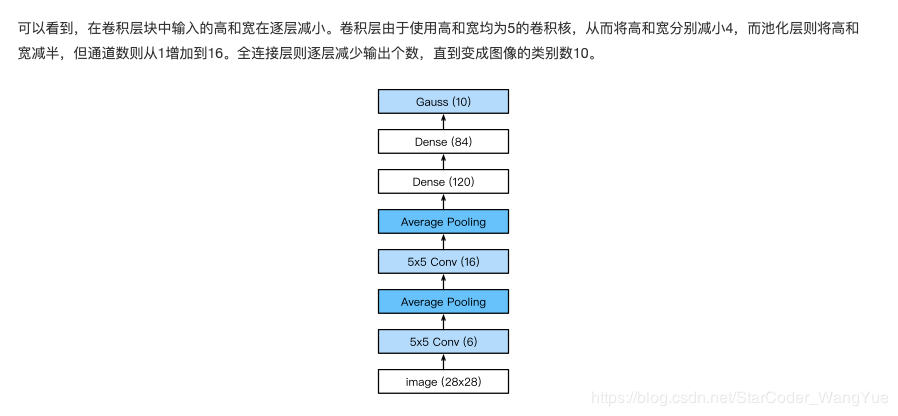
在这里插入图片描述

3.卷积神经网络进阶

LeNet: 在大的真实数据集上的表现并不尽如⼈意。
1.神经网络计算复杂。
2.还没有⼤量深⼊研究参数初始化和⾮凸优化算法等诸多领域。

机器学习的特征提取:手工定义的特征提取函数
神经网络的特征提取：通过学习得到数据的多级表征，并逐级表⽰越来越抽象的概念或模式。

神经网络发展的限制:数据、硬件

AlexNet

首次证明了学习到的特征可以超越⼿⼯设计的特征，从而⼀举打破计算机视觉研究的前状。
特征：

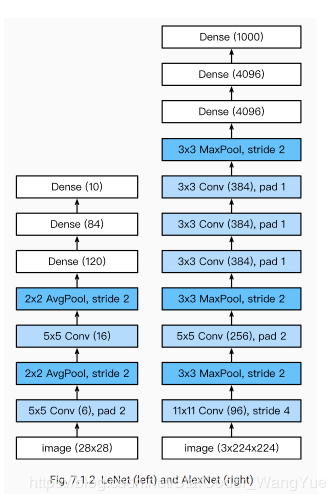
8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。
将sigmoid激活函数改成了更加简单的ReLU激活函数。
用Dropout来控制全连接层的模型复杂度。
引入数据增强，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。
在这里插入图片描述

import time
import torch
from torch import nn, optim
import torchvision
import numpy as np
import sys
sys.path.append("/home/kesci/input/") 
import d2lzh1981 as d2l
import os
import torch.nn.functional as F
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 96, 11, 4), # in_channels, out_channels, kernel_size, stride, padding
            nn.ReLU(),
            nn.MaxPool2d(3, 2), # kernel_size, stride
            # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
            nn.Conv2d(96, 256, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            # 连续3个卷积层，且使用更小的卷积窗口。除了最后的卷积层外，进一步增大了输出通道数。
            # 前两个卷积层后不使用池化层来减小输入的高和宽
            nn.Conv2d(256, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
         # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
        self.fc = nn.Sequential(
            nn.Linear(256*5*5, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            #由于使用CPU镜像，精简网络，若为GPU镜像可添加该层
            #nn.Linear(4096, 4096),
            #nn.ReLU(),
            #nn.Dropout(0.5),
            # 输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
            nn.Linear(4096, 10),
        )
    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output
net = AlexNet()
print(net)

使用重复元素的网络（VGG）

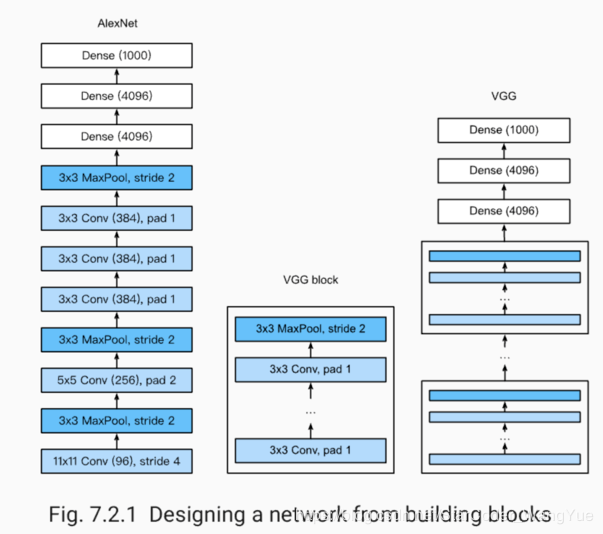
VGG：通过重复使⽤简单的基础块来构建深度模型。
Block:数个相同的填充为1、窗口形状为的卷积层,接上一个步幅为2、窗口形状为的最大池化层。
卷积层保持输入的高和宽不变，而池化层则对其减半。

在这里插入图片描述

def vgg_block(num_convs, in_channels, out_channels): #卷积层个数，输入通道数，输出通道数
    blk = []
    for i in range(num_convs):
        if i == 0:
            blk.append(nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
        else:
            blk.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
        blk.append(nn.ReLU())
    blk.append(nn.MaxPool2d(kernel_size=2, stride=2)) # 这里会使宽高减半
    return nn.Sequential(*blk)
def vgg(conv_arch, fc_features, fc_hidden_units=4096):
    net = nn.Sequential()
    # 卷积层部分
    for i, (num_convs, in_channels, out_channels) in enumerate(conv_arch):
        # 每经过一个vgg_block都会使宽高减半
        net.add_module("vgg_block_" + str(i+1), vgg_block(num_convs, in_channels, out_channels))
    # 全连接层部分
    net.add_module("fc", nn.Sequential(d2l.FlattenLayer(),
                                 nn.Linear(fc_features, fc_hidden_units),
                                 nn.ReLU(),
                                 nn.Dropout(0.5),
                                 nn.Linear(fc_hidden_units, fc_hidden_units),
                                 nn.ReLU(),
                                 nn.Dropout(0.5),
                                 nn.Linear(fc_hidden_units, 10)
                                ))
    return net
net = vgg(conv_arch, fc_features, fc_hidden_units)
X = torch.rand(1, 1, 224, 224)
# named_children获取一级子模块及其名字(named_modules会返回所有子模块,包括子模块的子模块)
for name, blk in net.named_children(): 
    X = blk(X)
    print(name, 'output shape: ', X.shape)
ratio = 8
small_conv_arch = [(1, 1, 64//ratio), (1, 64//ratio, 128//ratio), (2, 128//ratio, 256//ratio), 
                   (2, 256//ratio, 512//ratio), (2, 512//ratio, 512//ratio)]
net = vgg(small_conv_arch, fc_features // ratio, fc_hidden_units // ratio)
print(net)

⽹络中的⽹络（NiN）

LeNet、AlexNet和VGG：先以由卷积层构成的模块充分抽取空间特征，再以由全连接层构成的模块来输出分类结果。
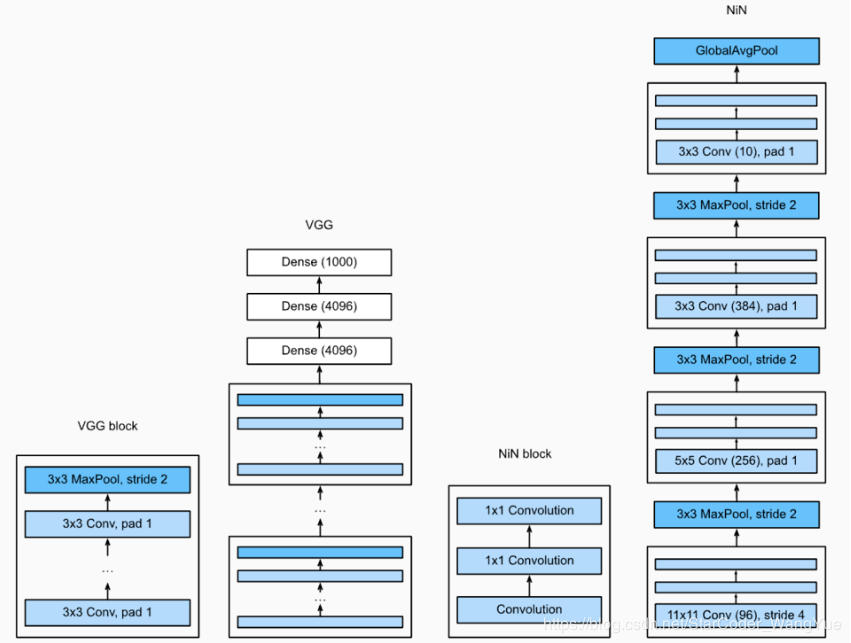
NiN：串联多个由卷积层和“全连接”层构成的小⽹络来构建⼀个深层⽹络。
⽤了输出通道数等于标签类别数的NiN块，然后使⽤全局平均池化层对每个通道中所有元素求平均并直接⽤于分类。

在这里插入图片描述

1×1卷积核作用

1.放缩通道数：通过控制卷积核的数量达到通道数的放缩。
2.增加非线性。1×1卷积核的卷积过程相当于全连接层的计算过程，并且还加入了非线性激活函数，从而可以增加网络的非线性。
3.计算参数少

def nin_block(in_channels, out_channels, kernel_size, stride, padding):
    blk = nn.Sequential(nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding),
                        nn.ReLU(),
                        nn.Conv2d(out_channels, out_channels, kernel_size=1),
                        nn.ReLU(),
                        nn.Conv2d(out_channels, out_channels, kernel_size=1),
                        nn.ReLU())
    return blk
class GlobalAvgPool2d(nn.Module):
    # 全局平均池化层可通过将池化窗口形状设置成输入的高和宽实现
    def __init__(self):
        super(GlobalAvgPool2d, self).__init__()
    def forward(self, x):
        return F.avg_pool2d(x, kernel_size=x.size()[2:])
net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, stride=4, padding=0),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nin_block(96, 256, kernel_size=5, stride=1, padding=2),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nin_block(256, 384, kernel_size=3, stride=1, padding=1),
    nn.MaxPool2d(kernel_size=3, stride=2), 
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, stride=1, padding=1),
    GlobalAvgPool2d(), 
    # 将四维的输出转成二维的输出，其形状为(批量大小, 10)
    d2l.FlattenLayer())
X = torch.rand(1, 1, 224, 224)
for name, blk in net.named_children(): 
    X = blk(X)
    print(name, 'output shape: ', X.shape)
batch_size = 128
# 如出现“out of memory”的报错信息，可减小batch_size或resize
#train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
lr, num_epochs = 0.002, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)

NiN重复使⽤由卷积层和代替全连接层的1×1卷积层构成的NiN块来构建深层⽹络。
NiN去除了容易造成过拟合的全连接输出层，而是将其替换成输出通道数等于标签类别数的NiN块和全局平均池化层。
NiN的以上设计思想影响了后⾯⼀系列卷积神经⽹络的设计。

GoogLeNet

由Inception基础块组成。
Inception块相当于⼀个有4条线路的⼦⽹络。它通过不同窗口形状的卷积层和最⼤池化层来并⾏抽取信息，并使⽤1×1卷积层减少通道数从而降低模型复杂度。
可以⾃定义的超参数是每个层的输出通道数，我们以此来控制模型复杂度。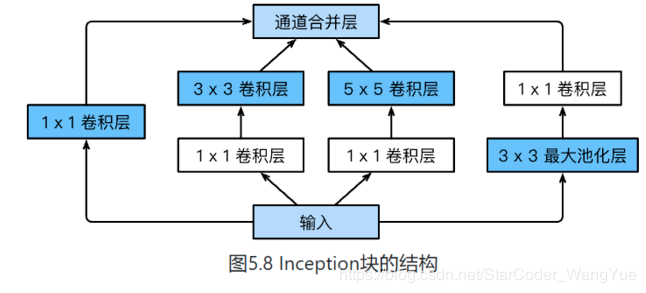在这里插入图片描述

class Inception(nn.Module):
    # c1 - c4为每条线路里的层的输出通道数
    def __init__(self, in_c, c1, c2, c3, c4):
        super(Inception, self).__init__()
        # 线路1，单1 x 1卷积层
        self.p1_1 = nn.Conv2d(in_c, c1, kernel_size=1)
        # 线路2，1 x 1卷积层后接3 x 3卷积层
        self.p2_1 = nn.Conv2d(in_c, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1 x 1卷积层后接5 x 5卷积层
        self.p3_1 = nn.Conv2d(in_c, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3 x 3最大池化层后接1 x 1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_c, c4, kernel_size=1)
    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1)  # 在通道维上连结输出

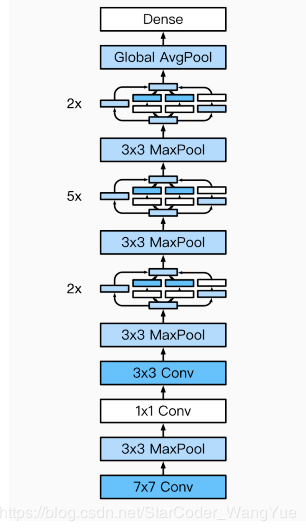
GoogLeNet模型

在这里插入图片描述

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   d2l.GlobalAvgPool2d())
net = nn.Sequential(b1, b2, b3, b4, b5, 
                    d2l.FlattenLayer(), nn.Linear(1024, 10))
net = nn.Sequential(b1, b2, b3, b4, b5, d2l.FlattenLayer(), nn.Linear(1024, 10))
X = torch.rand(1, 1, 96, 96)
for blk in net.children(): 
    X = blk(X)
    print('output shape: ', X.shape)
#batchsize=128
batch_size = 16
# 如出现“out of memory”的报错信息，可减小batch_size或resize
#train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)

参考资料：
https://www.kesci.com/org/boyuai/project/5e4632f95f2816002ceee482
https://www.kesci.com/org/boyuai/project/5e4633025f2816002ceee49c
https://www.kesci.com/org/boyuai/project/5e469c5d5f2816002cf0727f

作者：StarCoder_Yue

网络基础动手学 lenet 学习卷积神经网络深度学习神经网络卷积