在 pytorch 中实现计算图和自动求导
前言:
今天聊一聊 pytorch 的计算图和自动求导,我们先从一个简单例子来看,下面是一个简单函数建立了 yy 和 xx 之间的关系
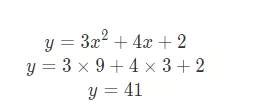
然后我们结点和边形式表示上面公式:

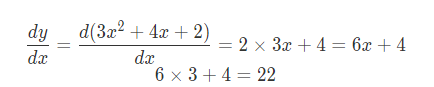
上面的式子可以用图的形式表达,接下来我们用 torch 来计算 x 导数,首先我们创建一个 tensor 并且将其requires_grad设置为True表示随后反向传播会对其进行求导。
x = torch.tensor(3.,requires_grad=True)
然后写出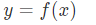
y = 3*x**2 + 4*x + 2
y.backward()
x.grad
通过调用y.backward()来进行求导,这时就可以通过x.grad来获得x的导数
x.requires_grad_(False)
可以通过requires_grad_让x不参与到自动求导
for epoch in range(3):
y = 3*x**2 + 4*x + 2
y.backward()
print(x.grad)
x.grad.zero_()
如果这里没有调用x.grad_zero_()就是把每次求导数和上一次求导结果进行累加。


相对于 z 对 x 求偏导时,我们可以将 y 看成常数,这样 x 导数是 1 那么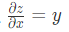
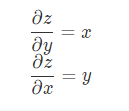
x = torch.tensor([1.,2.,3.],requires_grad=True)
y = x * 2 + 3
z = y **2
out = z.mean()
out.backward()
print(out) #tensor(51.6667, grad_fn=<MeanBackward0>)
print(x.grad) #tensor([ 6.6667, 9.3333, 12.0000])
对于一个简单的网络,我们可以手动计算梯度,但是如果摆在你面前的是一个有152 层的网络怎么办?或者该网络有多个分支。这时你的计算复杂程度可想而知。接下来会带来更深入自动求导内部机制
到此这篇关于在 pytorch 中实现计算图和自动求导的文章就介绍到这了,更多相关 pytorch 计算图 内容请搜索软件开发网以前的文章或继续浏览下面的相关文章希望大家以后多多支持软件开发网!
相关文章
Cynthia
2020-09-01
Abina
2021-05-24
Manda
2020-04-16
Kande
2023-05-27
Tricia
2023-05-27
Tani
2023-07-20
Kande
2023-07-20
Roselani
2023-07-20
Vivienne
2023-07-20
Summer
2023-07-20
Damara
2023-07-20
Linnea
2023-07-20
Xylona
2023-07-20
Radinka
2023-07-20
Dorothy
2023-07-20
Nicole
2023-07-20
Maleah
2023-07-21
Hellens
2023-07-21