【计算机组成原理】--浮点数的加减运算

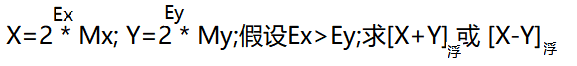1. Ex、Ey分别表示X、Y的阶码

Mx、My分别表示X、Y的尾数 Ex+y、Ex-y分别是[X+Y]、[X-Y]的阶码

***规格化概念:***规格化是指对上述尾数和(差)的规格化:设尾数和(差)是S，若满足,0.5≤|S|＜1，则认为是规格化的尾数和(差).
(采用变形补码法求尾数和(差)),结果形式:

浮点运算操作步骤: 0操作数的检查，看有无简化操作的可能(一般是可以跳过此步骤) 比阶码大小并完成对阶(小阶向大阶对齐) 尾数进行加或减运算 结果规格化 舍入处理 溢出判断

举个栗子~:

设x＝2^ 2×0.11011011,y=2^4×0.10101100，求[X-Y]浮

解:
1、0操作数检查（非0）
2、对阶：阶码对齐后才能加减。规则是阶码小的向阶码大的数对齐；

若△E＝0,表示两数阶码相等,即Eｘ＝Eｙ； 若△E>0,表示Eｘ>Eｙ； 若△E<0,表示Eｘ<Eｙ。 当Eｘ≠Eｙ 时,要通过尾数的移动以改变Eｘ或Eｙ,使之相等。

原则:小阶向大阶

Ex-y=00100
阶差=Ex-Ey=00 010- 00 100 =11 110（采用变形补码法）
即阶差为-2，Mx右移两位，Ex加2
x=00100 , 0.00110110（11）

3、尾数相加
00.00110110（11）
+11.01010100
=11.10001010（11)

4、结果规格化
左规一位: 尾数差=11.00010101(10)
左规一位，相当于尾数差乘以2，阶码减一阶，所以Ex-y=00 011

5 舍入处理(处理多出来的尾数即括号里面的10)
原则:0舍1入
         最高位为1，进1   最高位为0，截尾
11.00010101 处理后为:11.00010110

6、阶码溢出判断:
Ex-y=00 011(不溢出)
[X-Y]浮=-0.11101010*2^011

再举个栗子o(￣︶￣)o:

x=0.1101*2^01 y=-0.1010 * 2 ^11尾数和阶符都采用补码表示，都采用双符号位表示法。求[x+y]浮

1、对阶
    Ex-y=0011
    [x]浮=0001，00.1101
    [y]浮=0011，11.0110
    阶差=1110 即为-2
    Mx应当右移2位，
    [x]浮=0011，00.0011（01）

2、尾数相加
00.0110(01)+ 11.0110=11.1001(01)

3、结果规格化
左规一位，阶码减二一位
11.0010(10)     Ex-y=0010

4、舍入处理
11.0011

5、阶码判断溢出
未溢出
[X+Y]浮=-0.1101*2^10

总结一下:

求阶码差，对大阶 尾数求和 规格化(尾数和) 舍入处理 阶码判溢出

既然来啦~随手点个赞(๑•̀ㅂ•́)و✧呗

作者：Fight_adu

计算机组成 浮点数 浮点