RANSAC算法下两张图片的匹配效果——计算机视觉
RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。
RANSAC的基本假设是:
(1)数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
(2)“局外点”是不能适应该模型的数据;
(3)除此之外的数据属于噪声。
局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设。
RANSAC也做了以下假设:给定一组(通常很小的)局内点,存在一个可以估计模型参数的过程;而该模型能够解释或者适用于局内点。
RANSAC算法的输入是一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可信的参数。
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证:
1.首先我们先随机假设一小组局内点为初始值。然后用此局内点拟合一个模型,此模型适应于假设的局内点,所有的未知参数都能从假设的局内点计算得出。
2.用1中得到的模型去测试所有的其它数据,如果某个点适用于估计的模型,认为它也是局内点,将局内点扩充。
3.如果有足够多的点被归类为假设的局内点,那么估计的模型就足够合理。
4.然后,用所有假设的局内点去重新估计模型,因为此模型仅仅是在初始的假设的局内点估计的,后续有扩充后,需要更新。
5.最后,通过估计局内点与模型的错误率来评估模型。
整个这个过程为迭代一次,此过程被重复执行固定的次数,每次产生的模型有两个结局:
1、要么因为局内点太少,还不如上一次的模型,而被舍弃,
2、要么因为比现有的模型更好而被选用。
RANSAC loop:
1.随机选择四对匹配特征
2.根据DLT计算单应矩阵 H (唯一解)
3 .对所有匹配点,计算映射误差 ε=∥pi′,Hpi∥\varepsilon = \left \|{p_i'} ,H{p_i} \right \|ε=∥pi′,Hpi∥
4.根据误差阈值,确定inliers(例如3-5像素)
5.针对最大inliers集合,重新计算单应矩阵 H



1.基于ransac的sift匹配
python3.6+opencv3.3
转自 推杯问盏
import cv2
import numpy as np
def sift_kp(image):
gray_image = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)
sift=cv2.xfeatures2d.SIFT_create()
kp,des = sift.detectAndCompute(image,None)
kp_image = cv2.drawKeypoints(gray_image,kp,None)
return kp_image,kp,des
def get_good_match(des1,des2):
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2) #des1为模板图,des2为匹配图
matches = sorted(matches,key=lambda x:x[0].distance/x[1].distance)
good = []
for m, n in matches:
if m.distance 4:
ptsA= np.float32([kp1[m.queryIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
ptsB = np.float32([kp2[m.trainIdx].pt for m in goodMatch]).reshape(-1, 1, 2)
ransacReprojThreshold = 4
H, status =cv2.findHomography(ptsA,ptsB,cv2.RANSAC,ransacReprojThreshold);
imgOut = cv2.warpPerspective(img2, H, (img1.shape[1],img1.shape[0]),flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
return imgOut,H,status
img1 = cv2.imread(r'sift_img/8.png')
img2 = cv2.imread(r'sift_img/7.png')
_,kp1,des1 = sift_kp(img1)
_,kp2,des2 = sift_kp(img2)
goodMatch = get_good_match(des1,des2)
img3 = cv2.drawMatches(img1, kp1, img2, kp2, goodMatch[:5], None, flags=2)
#----or----
#goodMatch = np.expand_dims(goodMatch,1)
#img3 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, goodMatch[:5], None, flags=2)
cv2.imshow('img',img3)
cv2.waitKey(0)
cv2.destroyAllWindows()
2.基于ransac的harris匹配
转自Kissrabbit
#coding=utf-8
import numpy as np
import harris
import ransac
from PIL import Image
from pylab import *
import matplotlib.pyplot as plt
import win_unicode_console
win_unicode_console.enable()
img1 = np.array(Image.open('D:/ck/6.jpg').convert('L'))
img2 = np.array(Image.open('D:/ck/10.jpg').convert('L'))
wid = 9
harrisimg_1 = harris.compute_harris_response(img1) #计算Harris响应
filtered_coords_1 = harris.get_harris_points(harrisimg_1) #获取Harris角点的坐标
harris.plot_harris_points(img1, filtered_coords_1) #在图像中绘制Harris角点的位置
d1 = harris.get_descriptors(img1,filtered_coords_1,wid) #获取Harris角点的描述子
harrisimg_2 = harris.compute_harris_response(img2)
filtered_coords_2 = harris.get_harris_points(harrisimg_2)
harris.plot_harris_points(img2, filtered_coords_2)
d2 = harris.get_descriptors(img2,filtered_coords_2,wid)
print('strating matching')
match_points_coords_1 = []
match_points_coords_2 = []
matches = harris.match(d1,d2) #获取匹配关系,这个函数得到的匹配精度不太好。如果想获得更加精确些的匹配,可以调用harris.match_twosided(d1,d2)
###获取匹配点
for i,m in enumerate(matches):
if m > 0:
match_points_coords_1.append(filtered_coords_1[i])
match_points_coords_2.append(filtered_coords_2[m])
points_1 = np.array(match_points_coords_1).T
points_2 = np.array(match_points_coords_2).T
X = np.concatenate([points_1,np.ones([1,points_1.shape[1]])])
Y = np.concatenate([points_2,np.ones([1,points_2.shape[1]])])
###利用这些匹配点计算两个图的单应矩阵
H,X_,Y_ = ransac.homography(X,Y,10)
print(H)
###绘制在图片上的原始匹配
plt.figure()
plt.gray()
harris.plot_matches(img1,img2,filtered_coords_1,filtered_coords_2,matches)
show()
img3 = harris.appendimages(img1,img2)
img3 = np.vstack((img3,img3)) #np.vstack()是垂直地把数组拼接在一起
imshow(img3)
###绘制经过优化后的匹配
for i in range(X_.shape[1]):
plot([X_[1][i],Y_[1][i]+img1.shape[1]],[X_[0][i],Y_[0][i]],'r')
axis('off')
show()
五、实验结果与分析
1.数据集
(前四个为景深丰富,后五个为景深单一)

本次实验我选用图1 5作为景深丰富,图6 10作为景深单一
因为sift的精度较高看实验现象不够明显,所以我多使用了harris角点检测来作为实验。
(1)景深丰富组
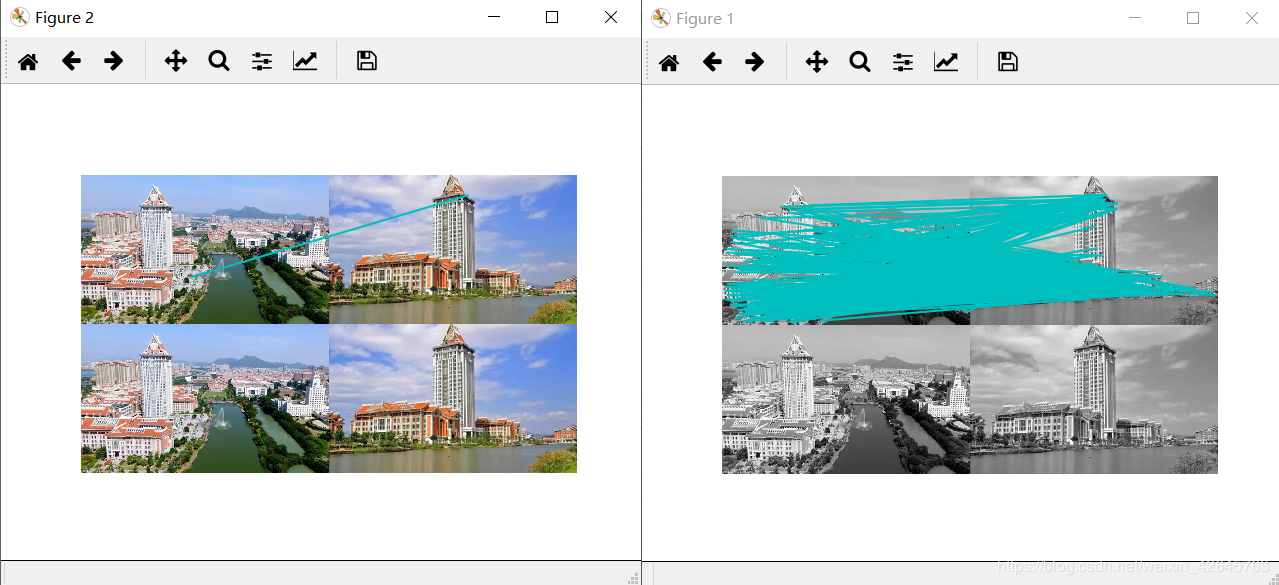
左图为sift匹配效果,右图为harris匹配效果
基于ransac算法的harris
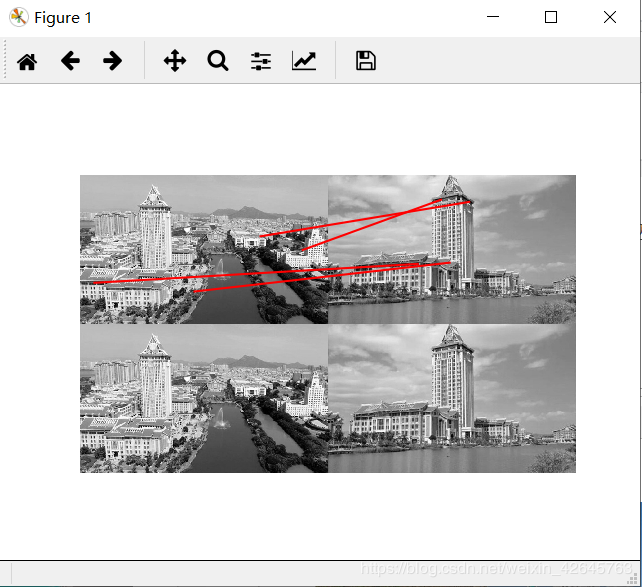
基于ransac算法的sift
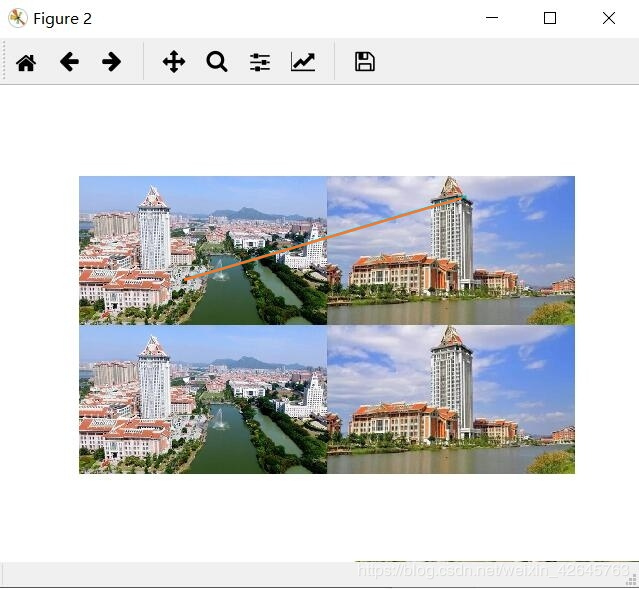
(2)景深单一组
左图为sift匹配效果,右图为harris算法效果
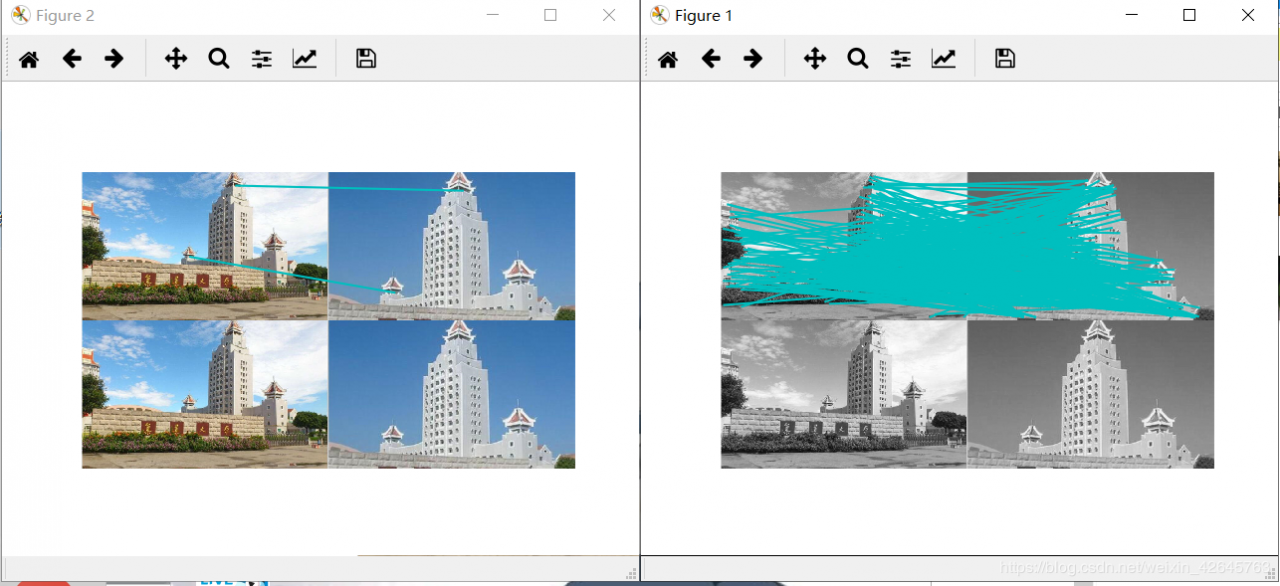
基于ransac算法的harris
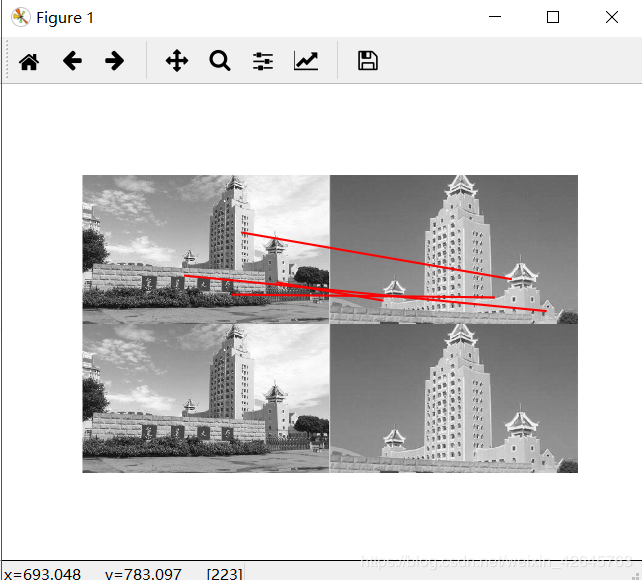
基于ransac算法的sift
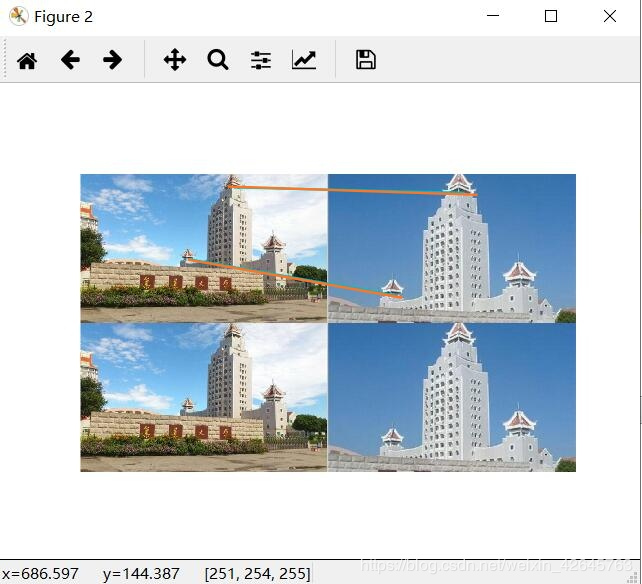
分析:RANSAC算法智能描述同一平面的问题,当图片处于不同平面时,非常容易出错,在harris匹配前提下,以上经过筛选的几条,基本上都出错了。而在sift特征匹配算法中,除了第一组图片景深高,因为处于不同平面匹配效果很差,连RANSAC优化以后都没有找出以外,景深单一组的sift算法匹配正确率高,优化效果也好。之所以没有把全部数据集的效果都放出来,是因为数据集中其他的sift匹配效果也并不好,不是匹配错就是没有匹配,应该是我数据集采集得不好。
六、总结RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。
RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。
RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC算法因为需要进行大量的迭代计算和数据处理,因此在某些复杂场景的拼接过程中,效率会比较低下。在本次实验可以看出优化的效果并不是很好,因为一开始给的匹配就不太好,如果匹配精度比较好的话,优化的结果应该会更好一点。
作者:蔚玄荆