机器学习实战：逻辑回归+梯度下降
使用梯度下降的方法进行逻辑回归实战：
作者：要好好学习呀！
问题说明：
这里将建立一个逻辑回归模型来预测一个学生是否被大学录取。
假设你是一个大学的管理员，你想根据两次考试的结果来决定每个申请人的录取机会，你有以前的申请人的历史数据。可以用历史数据作为逻辑回归的训练集。对于每一个样本,有两次考试的申请人的成绩和录取决定。建立一个分类模型，根据考试成绩估计入学概率。
数据链接：
链接:https://pan.baidu.com/s/1-pjwe1ogk30WpzN4Qg1NZA 密码:wqmt
完整代码实现如下：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pdData = pd.read_csv('/Users/hxx/Downloads/LogiReg_data.txt', header=None, names=['Exam1', 'Exam2', 'Admitted'], engine='python')
#header: 指定第几行作为列名(忽略注解行)，如果没有指定列名，默认header=0; 如果指定了列名header=None
#names 指定列名，如果文件中不包含header的行，应该显性表示header=None。这边列名为'Exam1', 'Exam2', 'Admitted'三列
print(pdData.head())#head()函数默认读取前五行
print(pdData.shape)#数据文件100行3列
positive = pdData[pdData['Admitted']==1]
negative = pdData[pdData['Admitted']==0]
plt.figure(figsize=(10,5))#设置画布
plt.scatter(positive['Exam1'], positive['Exam2'], c='b', marker='o', label='Admitted')#绘制散点图positive的点，Exam1和Exam2组成一个点
plt.scatter(negative['Exam1'], negative['Exam2'], c='r', marker='x', label='Not Admitted')#绘制散点图negative的点
plt.legend()# 添加图例（也就是图中右上角positive和negative的解释）
plt.xlabel('Exam1 Score')#添加x轴标签
plt.ylabel('Exam2 Score')#添加y轴标签
plt.show()
#定义sigmoid函数
def sigmoid(z):
return 1/(1+np.exp(-z))
nums = np.arange(-10,10,step=1)#随机取-10到10之间数值步长为1
plt.figure(figsize=(12,4))#设置画布
plt.plot(nums,sigmoid(nums),c='r')#sigmoid函数画图展示，nums表示x，sigmoid（nums）表示的y，x和y确定一点组成sigmoid函数图像
plt.show()
#定义模型h(x)
def model(X,theta):
return sigmoid(np.dot(X,theta.T))#将theta转置与x相乘，在代入sigmoid函数中得到模型。X是100*3列，theta是一行三列
#取数据
pdData.insert(0,'ones',1) #给数据添加一列，列名为ones，在第0列添加，数值为1，也就相当于x_0的系数theta_0
orig_data = pdData .as_matrix() # 将数据转变成矩阵形式
cols = orig_data .shape[1]#shape[0]就是读取矩阵第一维度的长度，相当于行数；shape[1]就是读取矩阵第二维度的长度，相当于列数，shape[1]=4
X = orig_data[:,0:cols-1]#逗号前冒号表示所有值，0:cols-1表示取第0列到（clos-1）列不包括cols-1这一列
y = orig_data[:,cols-1:cols]
theta = np.zeros([1,3])#这边设置theta值均为0，一行三列和x的一行三列相对应
print(X)
print(y)
print(theta)
#定义损失函数
#这边就是逻辑回归中的损失函数，逻辑回归详情可以参考：https://blog.csdn.net/hxx123520/article/details/104313032第四部分详细说明
def cost(X,y,theta):#对应于J(theta)
left = np.multiply(-y,np.log(model(X,theta)))#np.multiply对应位置相乘
right = np.multiply(1-y,np.log(1-model(X,theta)))
return np.sum(left-right)/(len(X))
print(cost(X,y,theta))
#根据梯度计算公式计算梯度
#也就是损失函数对theta求偏导，得到的就是梯度
def gradient(X,y,theta):
grad = np.zeros(theta.shape) # 定义初始化梯度,一行三列
#print(grad.shape)
error = (model(X, theta) - y).ravel()# 一行一百列。error=（预测y-真实值y）
#print(error)
# print(len(theta .ravel()))#3
for j in range(len(theta.ravel())):
term = np.multiply(error, X[:, j])#x[:,j] 取第j列的所有x样本
grad[0, j] = np.sum(term) / len(X)#这边的grad就是一行三列。grad[0,0]表示第0行第0列，for循环不断更新j，最终就是[0，2]表示0行2列
#print(grad)
return grad
#numpy中的ravel()、flatten()、squeeze()都有将多维数组转换为一维数组的功能，区别：
#ravel()：如果没有必要，不会产生源数据的副本。这边的error就是通过ravel函数将一百行一列拉成一行100列
#flatten()：返回源数据的副本
#squeeze()：只能对维数为1的维度降维
#三种梯度下降方法与三种停止策略
#三种停止策略
STOP_ITER=0 #根据指定的迭代次数来停止，更新一次参数相当于一次迭代
STOP_COST=1 #根据损失，每次迭代看一下迭代之前和之后的目标函数（损失值）的变化，没啥变化的话，可以停止
STOP_GRAD=2 #根据梯度，梯度变化贼小贼小
#设定三种不同的停止策略
def stopCriterion(type,value,threshold):
if type == STOP_ITER: return value > threshold #threshold指的是指定的迭代次数
elif type ==STOP_COST: return abs(value[-1]-value[-2]) < threshold#threshold指的损失函数的阈值，如果小于这个值就停止
elif type == STOP_GRAD: return np.linalg.norm(value) = n :
k=0
X,y=shuffleData(data)
theta=theta-alpha * grad#theta是一行三列，减去alpha*grad的一行三列，也就是更新后的theta
costs.append(cost(X,y,theta))#将损失值添加到costs中。append() 方法向列表的尾部添加一个新的元素。
i+=1;
if stoptype==STOP_ITER: value=i
if stoptype==STOP_COST:value=costs
if stoptype==STOP_GRAD:value=grad
if stopCriterion(stoptype,value,thresh):break
return theta,i-1,costs,grad,time.time()-init_time
def runExpe(data,theta,batchsize,stoptype,thresh,alpha):
theta, iter, costs, grad, dur = descent(data,theta,batchsize,stoptype,thresh,alpha)
if (data[:,1]>2).sum()>1:
name="Original"
else:
name="Scaled"
name=name + " data - learning rate: {} -".format(alpha)
if batchsize==n:
strDescType = "Gradient" #batchsize等于n是全局随机梯度下降
elif batchsize==1:
strDescType = "Stochastic" #batchsize等于1是随机梯度下降
else:
strDescType = "Mini-batch({})".format(batchsize)#小批量梯度下降
name = name + strDescType + " descent - stop :"
if stoptype==STOP_ITER:
strstop = "{} iterations".format(thresh)
elif stoptype==STOP_COST:
strstop = "cost change < {}".format(thresh)
else:
strstop = "gradient norm =0.5 else 0 for x in model(X,theta)]#设定阈值为0.5，大于0.5就可以入学
scaled_X = scaled_data[:,:3]
y = scaled_data[:,3]
prediction = predict(scaled_X,theta)
correct = [1 if ((a==1 and b==1) or (a==0 and b==0)) else 0 for (a,b) in zip(prediction,y)]#a对应的prediction值，b对应的真实值y
accuracy = (sum(map(int,correct)) % len(correct))#map() 会根据提供的函数对指定序列做映射。这边将correct映射为整数型在进行求和
print("accuracy {0}%".format(accuracy))
2.接下来详细的介绍一下不同的停止策略在上面代码中已经给出
2.1 批量梯度下降为例（batchsize=n=100）
停止条件为迭代次数5000
runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)
返回
*Original data - learning rate: 1e-06 -Gradient descent - stop :5000 iterations
Theta: [[-0.00027127 0.00705232 0.00376711]] - Iter: 5000 - Last cost: 0.63 - Duration: 0.95s
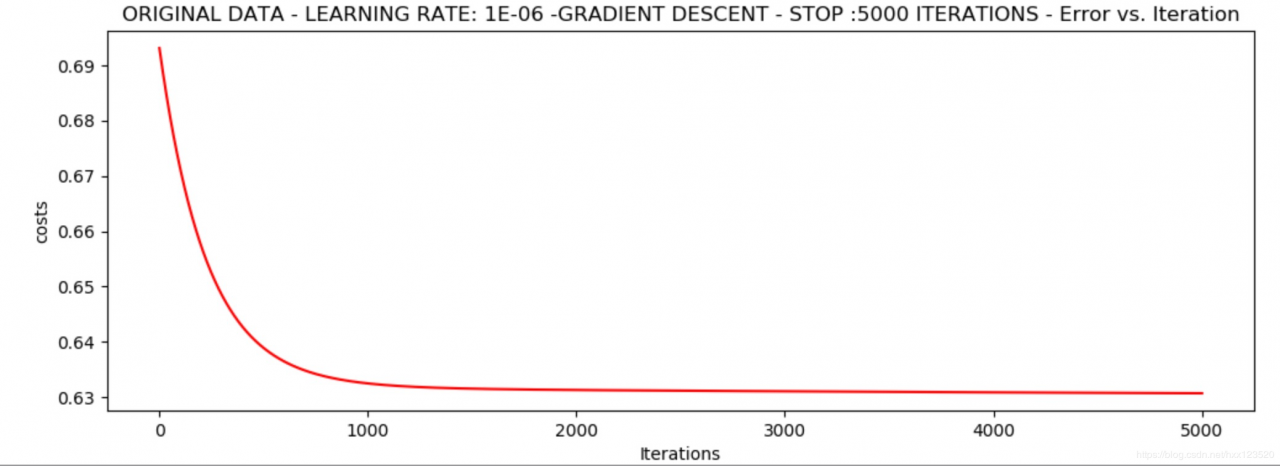看似损失值已经稳定在最低点0.63
设定阈值为0.000001，需要迭代110000次左右
runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)
返回
*Original data - learning rate: 0.001 -Gradient descent - stop :cost change < 1e-06
Theta: [[-5.13364014 0.04771429 0.04072397]] - Iter: 109901 - Last cost: 0.38 - Duration: 20.22s
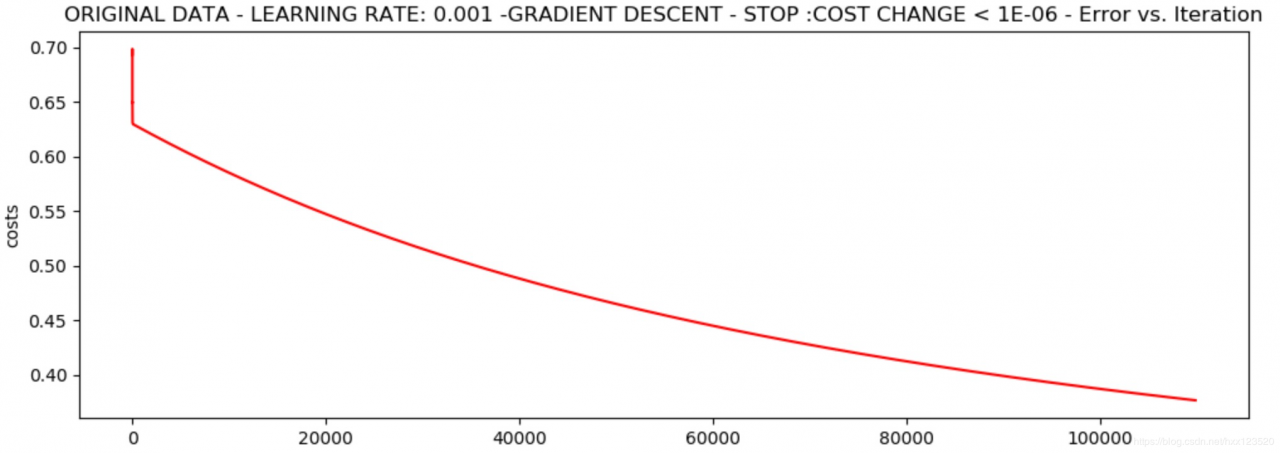损失值最低为0.38，似乎还可以进一步收敛
设定阈值0.05，需要迭代40000次左右
runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)
返回
*Original data - learning rate: 0.001 -Gradient descent - stop :gradient norm < 0.05
Theta: [[-2.37033409 0.02721692 0.01899456]] - Iter: 40045 - Last cost: 0.49 - Duration: 7.67s
损失值最小为0.49，似乎还可以进一步收敛
综上，基于批量梯度下降方法，上述三种停止条件得到的损失函数值为0.63、0.38和0.49，迭代次数分别为5000次、110000次和40000次，迭代次数越多，损失值越小
停止策略为迭代次数
3.1 随机梯度下降runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001)
返回
*Original data - learning rate: 0.001 -Stochastic descent - stop :5000 iterations
Theta: [[-0.38740891 0.09055956 -0.06431339]] - Iter: 5000 - Last cost: 0.91 - Duration: 0.31s
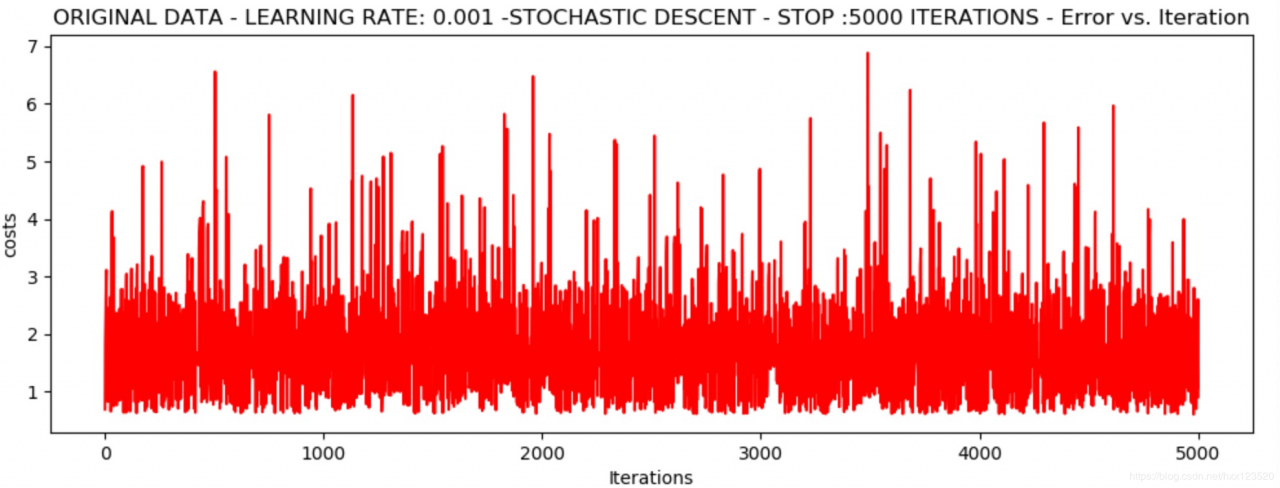波动非常大，迭代过程不稳定，这也是随机梯度下降的主要缺点
尝试降低学习率为0.000002，增加迭代次数为15000
runExpe(orig_data, theta, 1, STOP_ITER, thresh=15000, alpha=0.000002)
返回
*Original data - learning rate: 2e-06 -Stochastic descent - stop :15000 iterations
Theta: [[-0.00202428 0.00981444 0.00076997]] - Iter: 15000 - Last cost: 0.63 - Duration: 0.93s
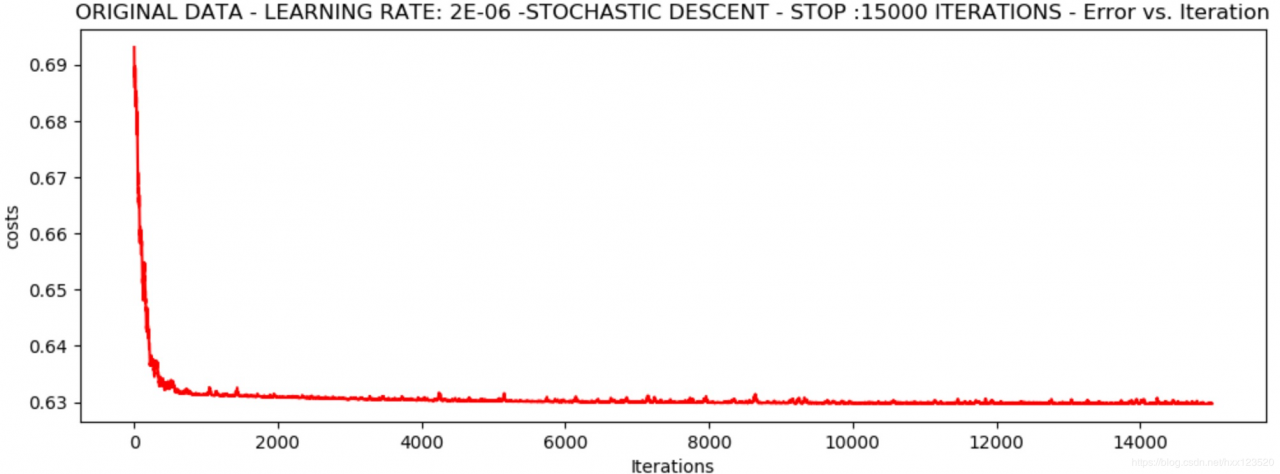效果要好一些，损失值似乎稳定在0.63,根据上面的结果可知，0.63不算是一个特别合理的值
#取样本为16
runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001)
返回
*Original data - learning rate: 0.001 -Mini-batch(16) descent - stop :15000 iterations
Theta: [[-1.03955915 0.01512354 0.00209486]] - Iter: 15000 - Last cost: 0.60 - Duration: 1.18s
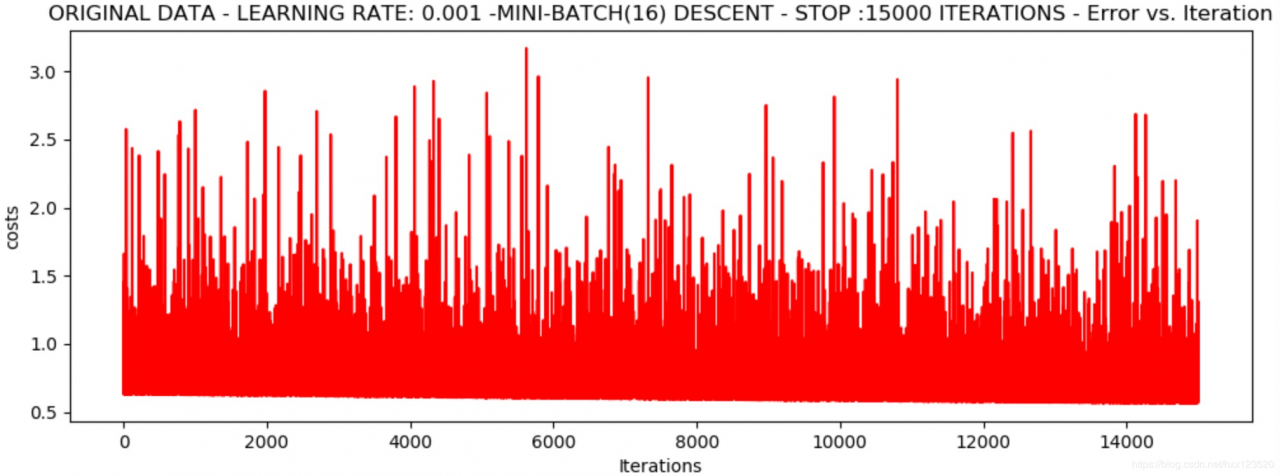上下波动，迭代过程不稳定
对于一些数据，降低学习率之后没有效果，迭代过程依旧不稳定
因此，可能不是模型本身的问题，而是数据本身的问题，尝试着对数据做一些变换，此处对数据进行标准化，用标准化后的数据求解
数据标准化问题，当数据发生浮动，先在数据层面上处理，先处理数据，再处理模型
from sklearn import preprocessing as pp
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])#scale 零均值单位方差，将数据转化为标准正态分布
接下来再来看看经过标准化处理后的数据得到的损失值图
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001) # 0.38
返回
*Scaled data - learning rate: 0.001 -Gradient descent - stop :5000 iterations
Theta: [[0.3080807 0.86494967 0.77367651]] - Iter: 5000 - Last cost: 0.38 - Duration: 0.98s
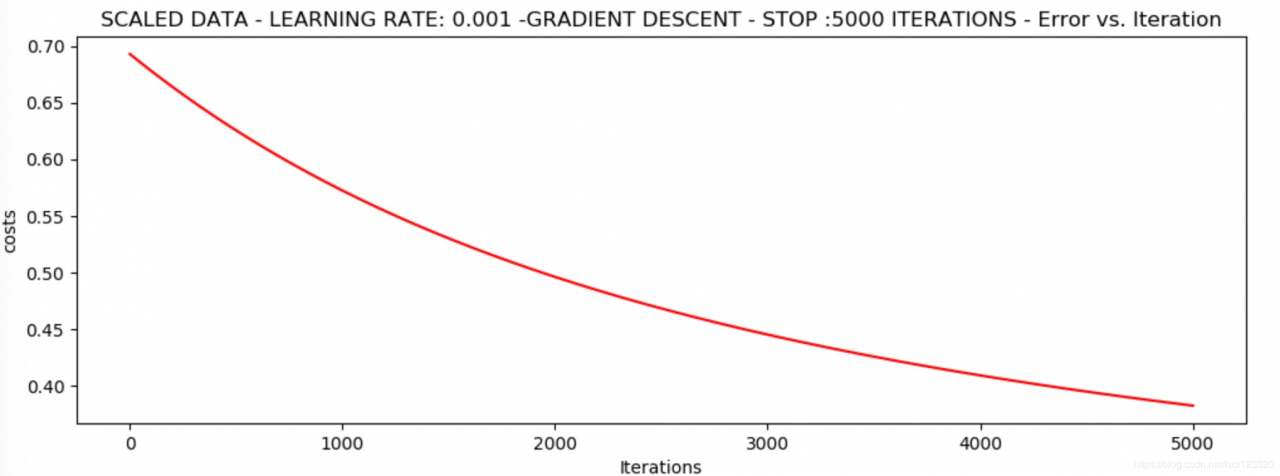
runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001) # 0.22
返回
*Scaled data - learning rate: 0.001 -Gradient descent - stop :gradient norm < 0.02
Theta: [[1.0707921 2.63030842 2.41079787]] - Iter: 59422 - Last cost: 0.22 - Duration: 12.18s
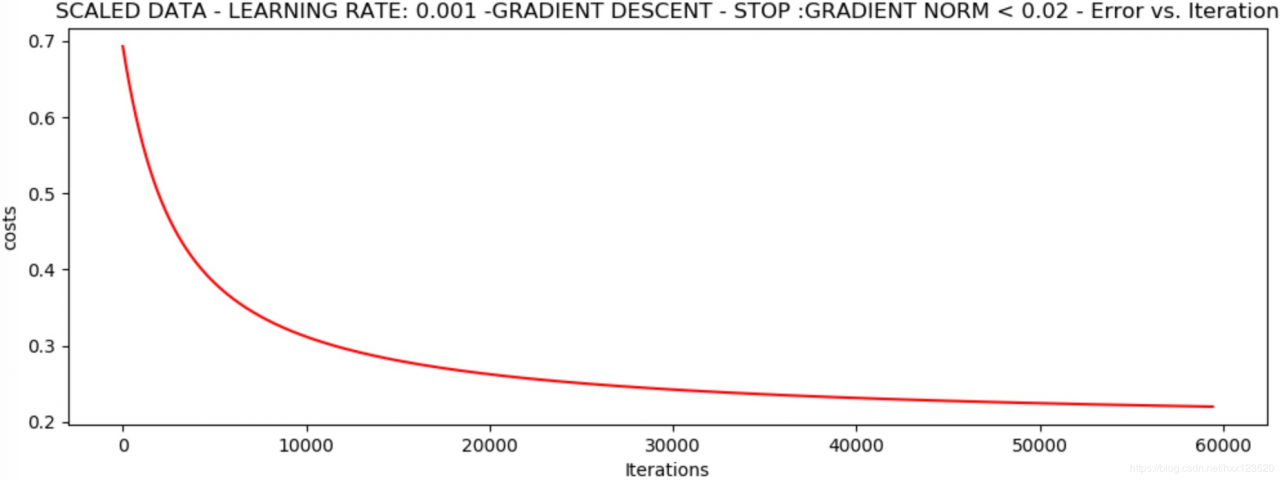
runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002 / 5, alpha=0.001) # 0.22
返回
*Scaled data - learning rate: 0.001 -Stochastic descent - stop :gradient norm < 0.0004
Theta: [[1.1486333 2.79230152 2.56637779]] - Iter: 72596 - Last cost: 0.22 - Duration: 5.63s
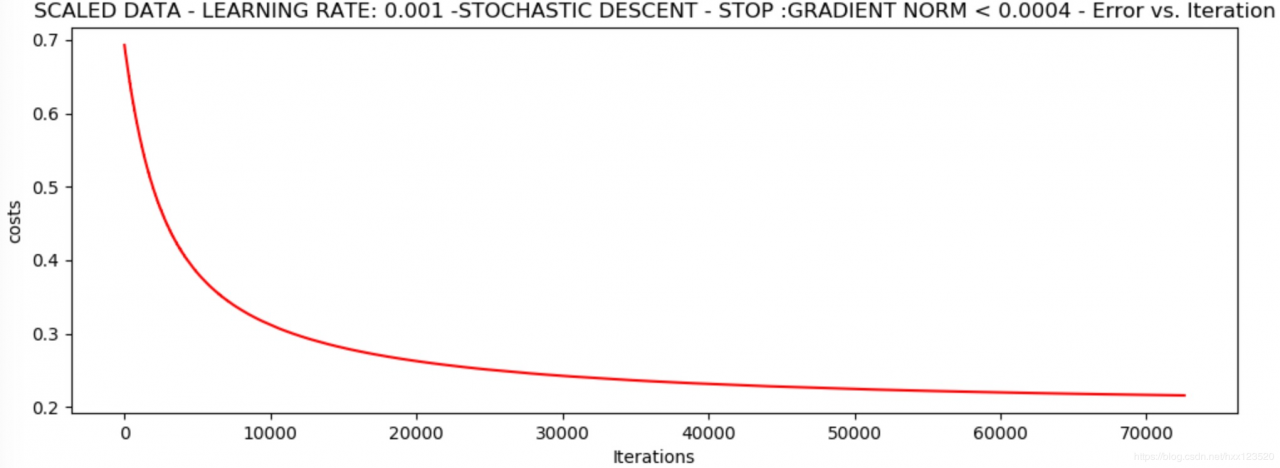
runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002 * 2, alpha=0.001)
返回
*Scaled data - learning rate: 0.001 -Mini-batch(16) descent - stop :gradient norm < 0.004
Theta: [[1.09946538 2.6858268 2.46623512]] - Iter: 63755 - Last cost: 0.22 - Duration: 6.40s
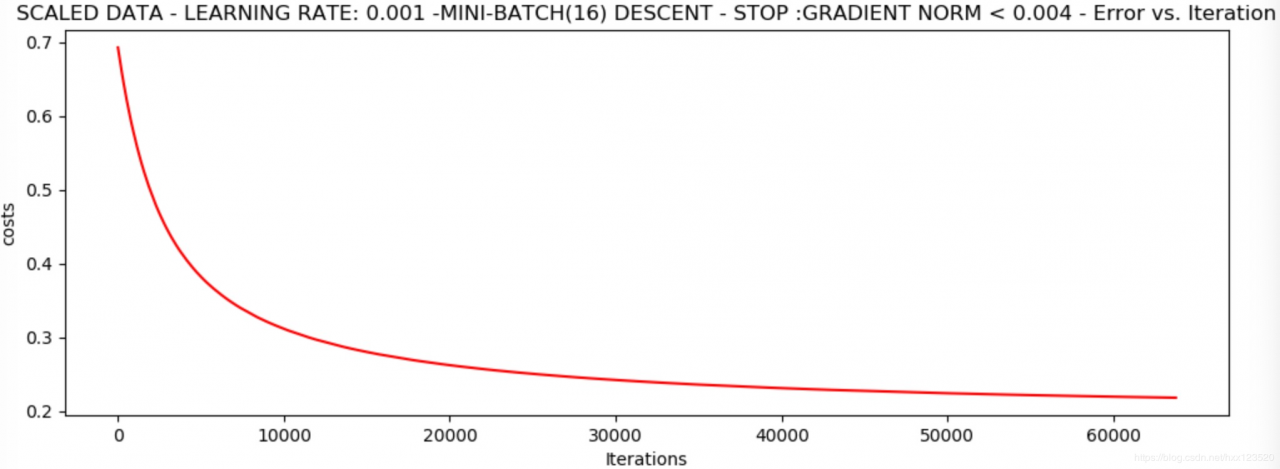可以发现，经过标准化处理的数据得到的损失值得到明显的改善。
作者：要好好学习呀！
