机器学习入门 --- 根据推导公式使用Python实现梯度下降与逻辑回归

关于梯度下降与逻辑回归，我在之前的文章中已经写过了公式推导，本文中将用python代码进行实现并做简单的实验

机器学习入门 — 梯度下降原理 机器学习入门 — 逻辑回归算法 案例概述

在这里我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。此大学会根据两次考试的结果来决定每个申请人的录取机会。大学里有以前的申请人的历史数据，可以用它作为逻辑回归的训练集。对于每一个学生例子，有两个考试的申请人的分数和录取决定。为了做到这一点，我们将建立一个分类模型，根据考试成绩估计入学概率。

数据准备 import os path = 'data' + os.sep + 'LogiReg_data.txt' #读取数据 --- 指定列名['Exam 1', 'Exam 2', 'Admitted'] pdData = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted']) pdData.head()

Exam 1	Exam 2	Admitted
34.623660	78.024693	0
30.286711	43.894998	0
35.847409	72.902198	0
60.182599	86.308552	1
79.032736	75.344376	1

使用 matplotlib 查看数据在图像中的形式

#对于Admitted进行定义，区分正负例 positive = pdData[pdData['Admitted'] == 1] # returns the subset of rows such Admitted = 1, i.e. the set of *positive* examples negative = pdData[pdData['Admitted'] == 0] # returns the subset of rows such Admitted = 0, i.e. the set of *negative* examples #可视化 #指定画图域 fig, ax = plt.subplots(figsize=(10,5)) #散点图 ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted') ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted') ax.legend() ax.set_xlabel('Exam 1 Score') ax.set_ylabel('Exam 2 Score')

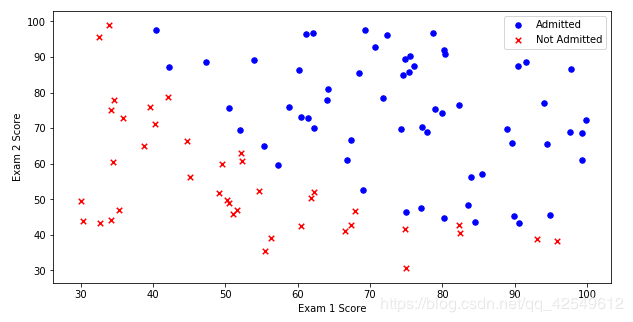
在这张图中，蓝色的点是被录取的，红色的 x 是不被录取的

逻辑回归

目标：建立分类器（求解出三个参数 θ0\theta_0θ0​ θ1\theta_1θ1​ θ2\theta_2θ2​）
设定阈值，根据阈值判断录取结果

要完成的模块 sigmoid : 映射到概率的函数（sigmoid函数） model : 返回预测结果值 cost : 根据参数计算损失 gradient : 计算每个参数的梯度方向 descent : 进行参数更新 accuracy: 计算精度

sigmoid函数

sigmoid : 映射到概率的函数

公式：
g(z)=11+e−z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1​

def sigmoid(z): return 1 / (1 + np.exp(-z)) g:R→[0,1]g:\mathbb{R} \to [0,1]g:R→[0,1] g(0)=0.5g(0)=0.5g(0)=0.5 g(−∞)=0g(- \infty)=0g(−∞)=0 g(+∞)=1g(+ \infty)=1g(+∞)=1

model : 返回预测结果值

公式：
hθ(x)=g(θTx)=11+e−θTxh_\theta (x) = g(\theta ^Tx)=\frac{1}{1+e^{-\theta ^Tx}}hθ​(x)=g(θTx)=1+e−θTx1​

def model(X, theta): return sigmoid(np.dot(X, theta.T))

设定数据组合方式：
(θ0θ1θ2)×(1x1x2)=θ0+θ1x1+θ2x2 \begin{array}{ccc} \begin{pmatrix}\theta_{0} & \theta_{1} & \theta_{2}\end{pmatrix} & \times & \begin{pmatrix}1\\ x_{1}\\ x_{2} \end{pmatrix}\end{array}=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2} (θ0​​θ1​​θ2​​)​×​⎝⎛​1x1​x2​​⎠⎞​​=θ0​+θ1​x1​+θ2​x2​

pdData.insert(0, 'Ones', 1) #构造与theta_0相匹配的数据 #设置X（训练数据）和y（目标变量） orig_data = pdData.as_matrix() #将数据的Pandas表示转换为数组，以便进一步计算 cols = orig_data.shape[1] #训练数据，取 0 ~ cols-1 的所有样本 X = orig_data[:,0:cols-1] #标签，取 cols-1 ~ cols 的所有样本 y = orig_data[:,cols-1:cols] #构造三个 theta参数 theta = np.zeros([1, 3])

数据到此就准备完成了。

损失函数

cost : 根据参数计算损失

公式：

将对数似然函数去负号

D(hθ(x),y)=−ylog⁡(hθ(x))−(1−y)log⁡(1−hθ(x)) D(h_\theta(x), y) = -y\log(h_\theta(x)) - (1-y)\log(1-h_\theta(x)) D(hθ​(x),y)=−ylog(hθ​(x))−(1−y)log(1−hθ​(x))
求平均损失
J(θ)=1n∑i=1nD(hθ(xi),yi) J(\theta)=\frac{1}{n}\sum_{i=1}^{n} D(h_\theta(x_i), y_i) J(θ)=n1​i=1∑n​D(hθ​(xi​),yi​)
D(hθ(x),y)D(h_\theta(x), y)D(hθ​(x),y)中：

左式：−ylog⁡(hθ(x))-y\log(h_\theta(x))−ylog(hθ​(x))

left = np.multiply(-y, np.log(model(X, theta)))

右式：−(1−y)log⁡(1−hθ(x))- (1-y)\log(1-h_\theta(x))−(1−y)log(1−hθ​(x))

right = np.multiply(-(1 - y), np.log(1 - model(X, theta)))

完整函数代码：

def cost(X, y, theta): #对数似然函数左式 left = np.multiply(-y, np.log(model(X, theta))) #对数似然函数右式 right = np.multiply(-(1 - y), np.log(1 - model(X, theta))) return np.sum(left + right) / (len(X)) 计算梯度

gradient : 计算每个参数的梯度方向

公式：
∂J∂θj=−1m∑i=1n(yi−hθ(xi))xij \frac{\partial J}{\partial \theta_j}=-\frac{1}{m}\sum_{i=1}^n (y_i - h_\theta (x_i))x_{ij} ∂θj​∂J​=−m1​i=1∑n​(yi​−hθ​(xi​))xij​

def gradient(X, y, theta): #构建梯度数据存储位置 grad = np.zeros(theta.shape) error = (model(X, theta)- y).ravel() for j in range(len(theta.ravel())): #for each parmeter term = np.multiply(error, X[:,j]) grad[0, j] = np.sum(term) / len(X) return grad 停止策略与梯度下降实例

根据 机器学习入门 — 梯度下降原理 中提到的三种梯度下降的方法，分别用代码展示出来：

#指定三种策略 #根据迭代次数 STOP_ITER = 0 #根据损失值 STOP_COST = 1 #根据梯度 STOP_GRAD = 2 def stopCriterion(type, value, threshold): #设定三种不同的停止策略 if type == STOP_ITER: return value > threshold elif type == STOP_COST: return abs(value[-1]-value[-2]) < threshold elif type == STOP_GRAD: return np.linalg.norm(value) < threshold

对数据进行洗牌

def shuffleData(data): np.random.shuffle(data) cols = data.shape[1] X = data[:, 0:cols-1] y = data[:, cols-1:] return X, y

descent : 进行参数更新

梯度下降求解

def descent(data, theta, batchSize, stopType, thresh, alpha): ''' data：数据 theta：学习参数 batchSize：可选三种梯度下降方法 stopType：停止策略 thresh：停止策略对应的阈值 alpha：学习率 ''' #初始化 init_time = time.time() i = 0 # 迭代次数 k = 0 # batch X, y = shuffleData(data) grad = np.zeros(theta.shape) # 计算的梯度 costs = [cost(X, y, theta)] # 损失值 while True: #计算梯度 grad = gradient(X[k:k+batchSize], y[k:k+batchSize], theta) k += batchSize #取batch数量个数据 if k >= n: k = 0 X, y = shuffleData(data) #重新洗牌 theta = theta - alpha*grad # 参数更新 costs.append(cost(X, y, theta)) # 计算新的损失 i += 1 if stopType == STOP_ITER: value = i elif stopType == STOP_COST: value = costs elif stopType == STOP_GRAD: value = grad if stopCriterion(stopType, value, thresh): break return theta, i-1, costs, grad, time.time() - init_time

训练启动及可视化函数

def runExpe(data, theta, batchSize, stopType, thresh, alpha): ''' data：数据 theta：学习参数 batchSize：可选三种梯度下降方法 stopType：停止策略 thresh：停止策略对应的阈值 alpha：学习率 ''' theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha) name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled" name += " data - learning rate: {} - ".format(alpha) #判断停止策略 if batchSize==n: strDescType = "Gradient" elif batchSize==1: strDescType = "Stochastic" else: strDescType = "Mini-batch ({})".format(batchSize) name += strDescType + " descent - Stop: " if stopType == STOP_ITER: strStop = "{} iterations".format(thresh) elif stopType == STOP_COST: strStop = "costs change < {}".format(thresh) else: strStop = "gradient norm < {}".format(thresh) name += strStop print ("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format( name, theta, iter, costs[-1], dur)) #画图 fig, ax = plt.subplots(figsize=(12,4)) ax.plot(np.arange(len(costs)), costs, 'r') ax.set_xlabel('Iterations') ax.set_ylabel('Cost') ax.set_title(name.upper() + ' - Error vs. Iteration') return theta 实验效果对比 不同的停止策略

根据迭代次数停止 — STOP_ITER

n=100 runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001)

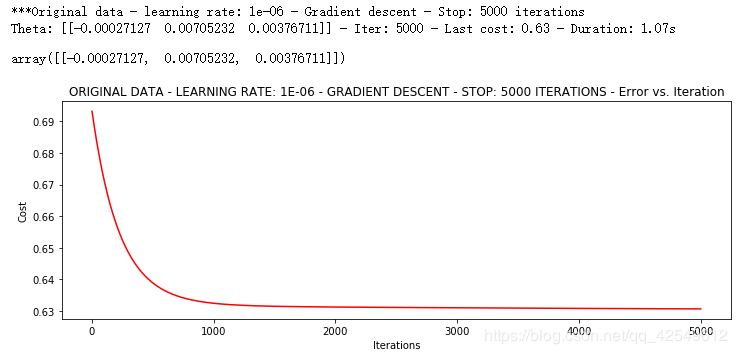
根据损失值停止 — STOP_COST

设定阈值 1E-6

n=100 runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001)

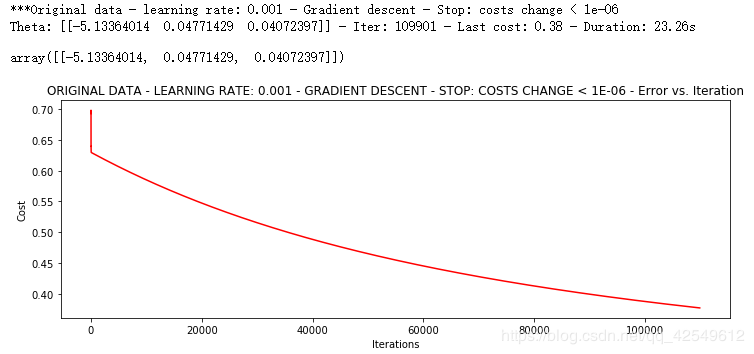
根据梯度变化停止 — STOP_GRAD

设定阈值0.05

n=100 runExpe(orig_data, theta, n, STOP_GRAD, thresh=0.05, alpha=0.001)

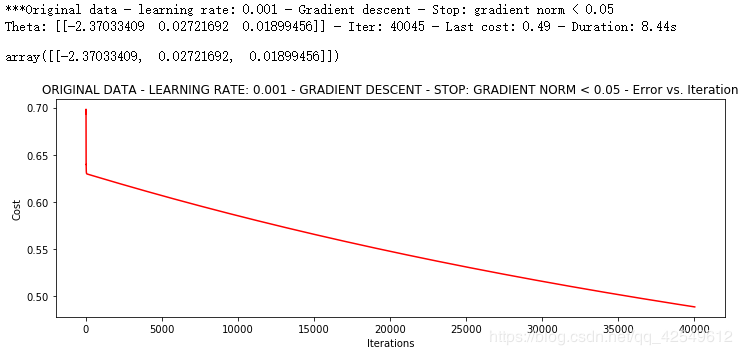
通过设置不同的停止策略发现，在训练中看到图像平稳，也还是可能会有很大的可优化空间，迭代次数的多少对模型训练的好坏起到很大的作用

不同的梯度下降方法

随机梯度下降

n=1 runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001)

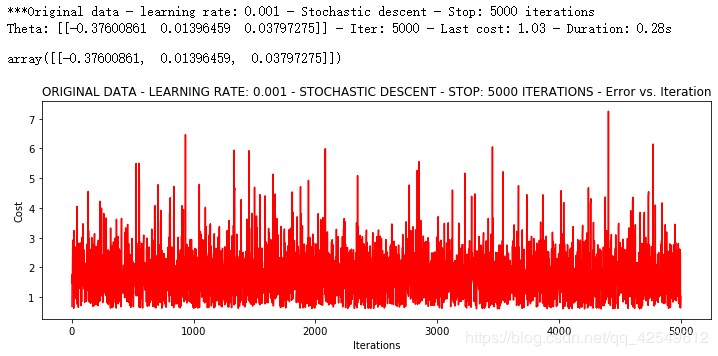
在此参数条件下，训练的过程很不稳定，模型无法收敛

n=1 runExpe(orig_data, theta, n, STOP_ITER, thresh=15000, alpha=0.000002)

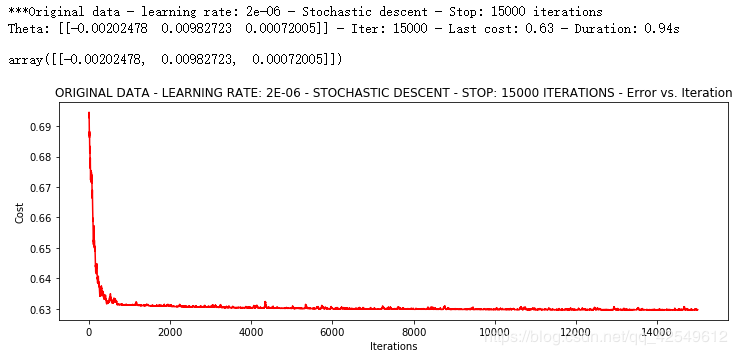
在设置了很小的学习率后，虽然模型收敛了，但稳定性依旧是比较差

小批量梯度下降

n=16 runExpe(orig_data, theta, n, STOP_ITER, thresh=15000, alpha=0.001)

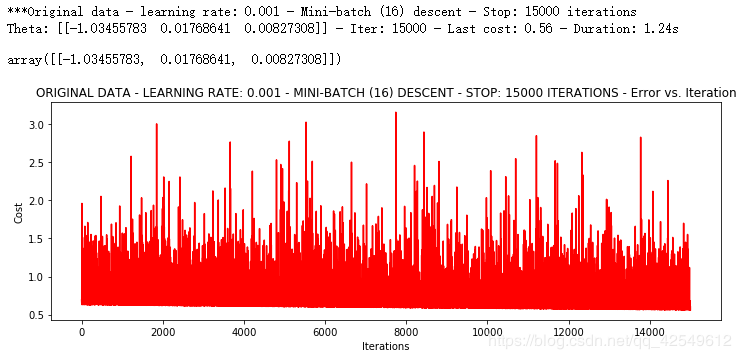学习率较大的情况下，损失值仍然是有比较大的浮动

如果训练结果有浮动，首先可先对数据下手，现在来尝试下对数据进行标准化

将数据按其属性(按列进行)减去其均值，然后除以其方差。最后得到的结果是，对每个属性/每列来说所有数据都聚集在0附近，方差值为1

在此使用Sklearn帮助将数据进行标准化

from sklearn import preprocessing as pp scaled_data = orig_data.copy() #数据标准化 scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3]) #开始训练 runExpe(scaled_data, theta, 16, STOP_ITER, thresh=5000, alpha=0.001)

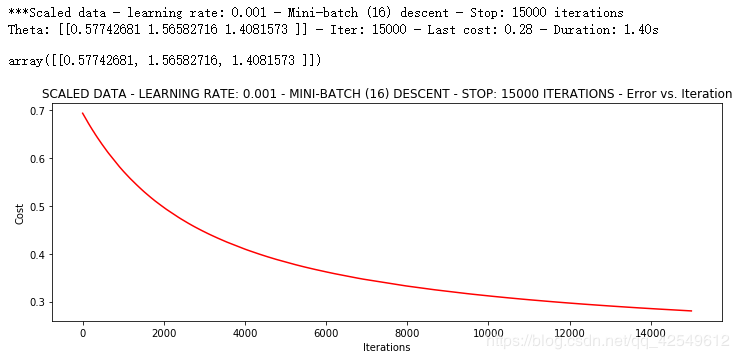
使用原始数据时，损失只能达到达到0.56，而我们得到了0.28
所以对数据做预处理也是非常重要的

精度

accuracy: 计算精度

在对比了这么多种方案之后，我们在看一下精度

#设定阈值 def predict(X, theta): return [1 if x >= 0.5 else 0 for x in model(X, theta)] scaled_X = scaled_data[:, :3] y = scaled_data[:, 3] predictions = predict(scaled_X, theta) correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)] accuracy = (sum(map(int, correct)) % len(correct)) print ('accuracy = {0}%'.format(accuracy))

最终精度可以达到89%

以上就是对梯度下降与逻辑回归的代码实现，可能在细节上不够精巧，但基本实现了该算法的推理功能，使得达到一个较为可观的结果

作者：六之

梯度下降 学习 用python 回归 梯度 机器学习入门 机器学习 Python 逻辑回归