机器学习之PCA

Octavia ·

更新时间:2024-11-11

· 701 次阅读

PCA（主成分分析法—Principal Component Analysis）一. 求数据的前n个主成分二. 高维数据映射为低维数据 一. 求数据的前n个主成分

紧接着上次汇报的内容：

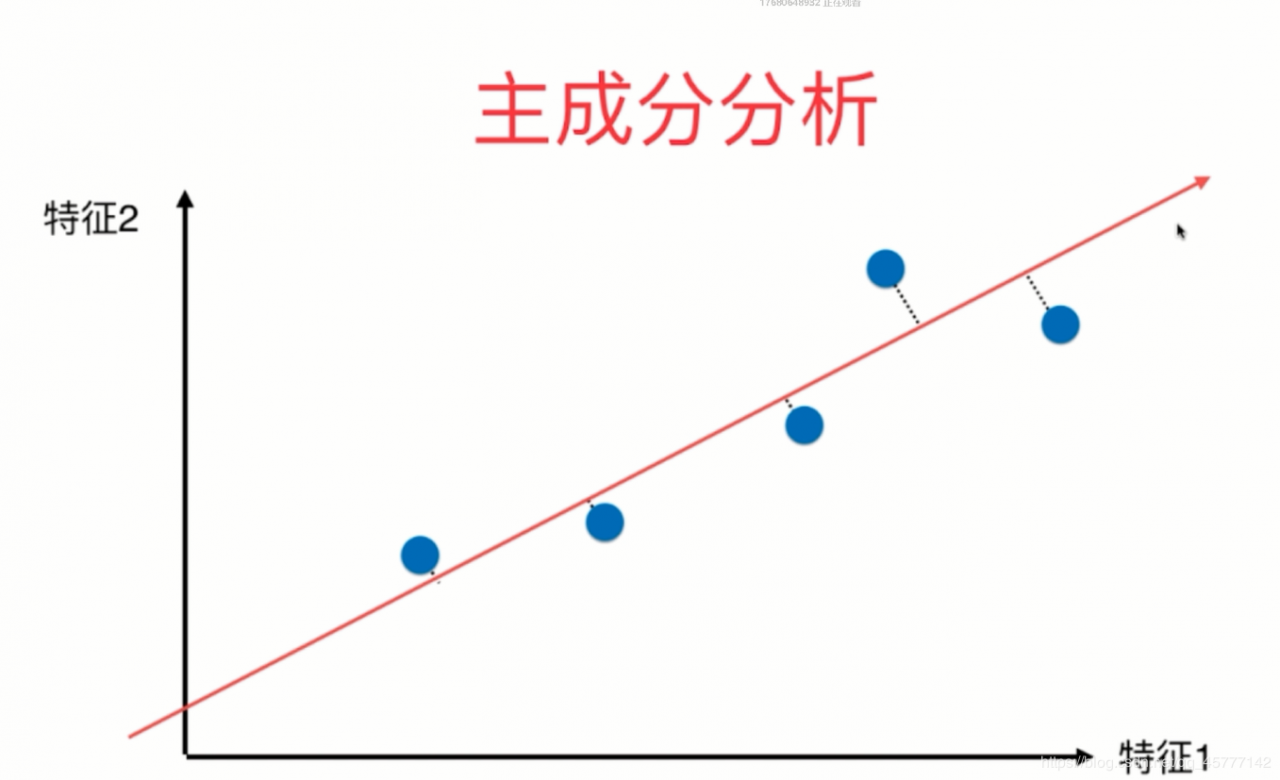
在这里插入图片描述
⟶将周围离散的点分别映射到这条直线上\stackrel{将周围离散的点分别映射到这条直线上}{\longrightarrow}⟶将周围离散的点分别映射到这条直线上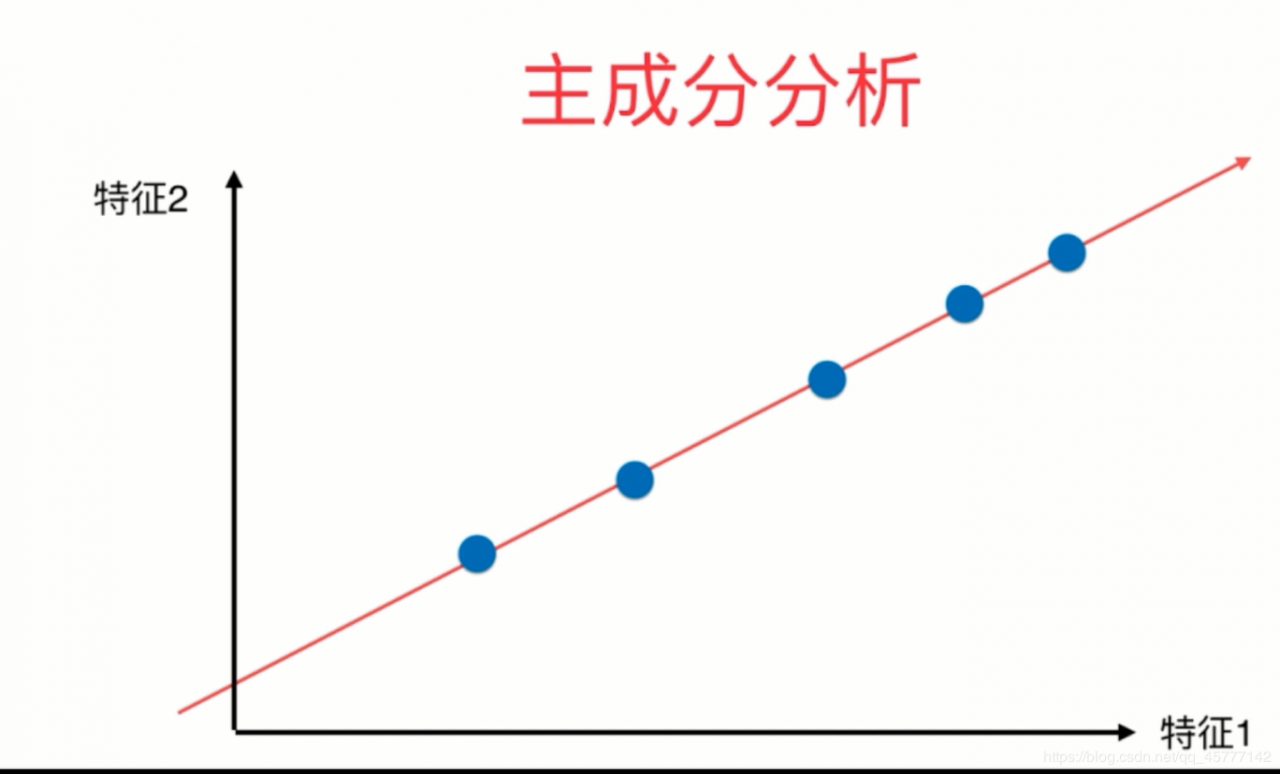
该直线所在的轴为我们的第一主成分，得到的结果就是这些样本点直接距离的方差是最大的

显然我们现在所求的不仅仅是局限在二维空间中，当维数增加时，我们如何求得下一个主成分？

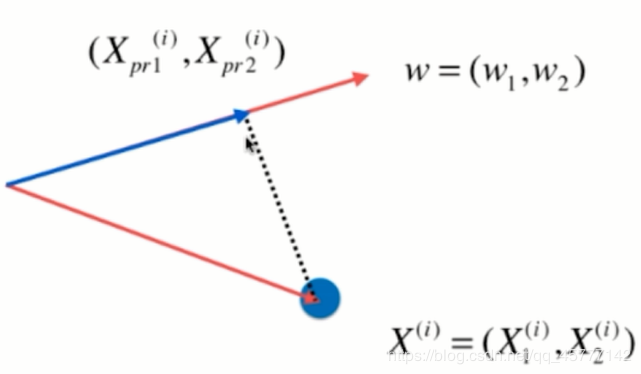	如左图所示,原来求直线向量：X(i)⋅w=∥X∥project(i)X^{(i)}\cdot w=\left \\| X\right \\|_{project}^{(i)}X(i)⋅w=∥X∥project(i) Xproject(i)=∥Xproject(i)∥⋅WX^{(i)}_{project} = \left \\| X^{(i)}_{project}\right \\|\cdot WXproject(i)=∥∥∥Xproject(i)∥∥∥⋅W
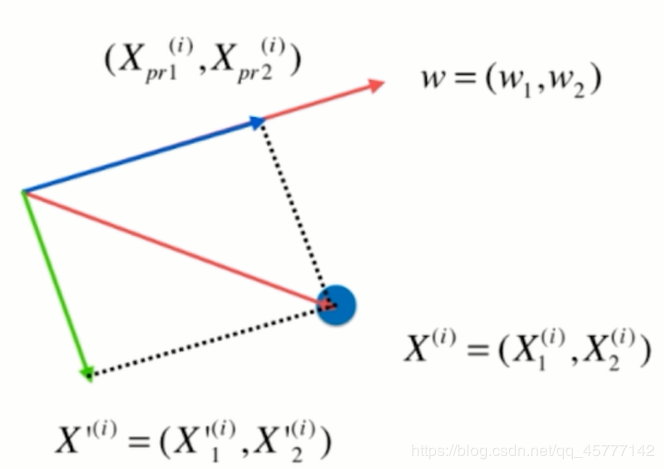	新求得的分量为（即图中绿色向量）：X′(i)=X(i)−Xproject(i)X^{'(i)} = X^{(i)} - X^{(i)}_{project}X′(i)=X(i)−Xproject(i)

其实道理是一样的：数据需要进行改变，将其在第一主成分上的分量去掉即可，原理为上方第二个图。

下面我们来编程实现这个前N个主成分的代码：

import numpy as np 
import matplotlib.pyplot as plt            #导入我们所需要的包
X=np.empty((100,2))                        #随机创建一个我们需要的二维数组
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0.,10.,size=100)
def demean(X):                             #将X数据均值归一化
           return X-np.mean(X,axis= 0)
X_demean = demean(X)
def f(w,X):                                #下面的步骤与之前的求简单二维PCA一模一样
           return np.sum((X.dot(w)**2))/len(X)
def df(w,v):
		   return X.T.dot(X.dot(w))*2. / len(X)
def direction(w):
           return w / np.linalg.norm(w)
def first_component(X,initial_w,eta,n_iters = 1e4,epsilon=1e-8): #梯度上升法
           w = direction(initial_w)
           cur_iter = 0
           while cur_iter < n_iters:
                      gradient = df(w,X)
                      last_w = w
                      w = w + eta *gradient
                      w = direction(w)
                      if (abs(f(w,X) - f(last_w,X)) < epsilon):
                                 break
                      cur_iter += 1
           return w
initial_w = np.random.random(X.shape[1])
eta = 0.001
result=first_component(df_math,X_demean,initial_w,eta)    
print(result)                           #此后我们设法减去第一主成分上的分量
X2 = np.empty(X.shape)
for  i in range(len(X)):
		    X2[i] = X[i] - X[i].dot(w) * w
w2 = first_component(X2,initial_w, eta)
print(w2)                               #此时输出的值如果和原来W相乘 结果为0（因为2个垂直向量的乘积为0）
print(w.dot(w2))                        #若结果为0  则该算法没毛病
#接下来我们尝试可以自己定义N的个数的N维度主成分分析法
def first_n_component(n , X, eta = 0.01, n_iters = 1e4, epsilon=1e-8):
			X_pca = X.copy()
			X_pca = demean(X_pca)
			res = []
			for i in range(n):
				initial_w = np.random.random(X_pca.shape[1])
				w = first_component(X_pca, initial_w, eta)
           		res.append(w)
           		X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w 
           	return res
#我们还是以二维的数据来验证一下
print(first_n_component(2, X))

二. 高维数据映射为低维数据

上述所求虽然实现了多维数据主成分轴所在向量，但是数据仍然是高维的，如何对数据进行降维处理？
我们先从矩阵入手：


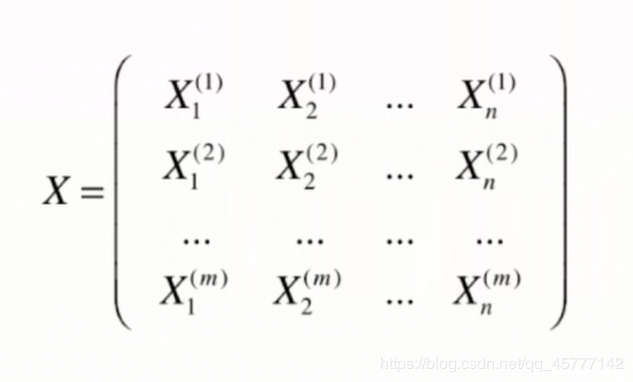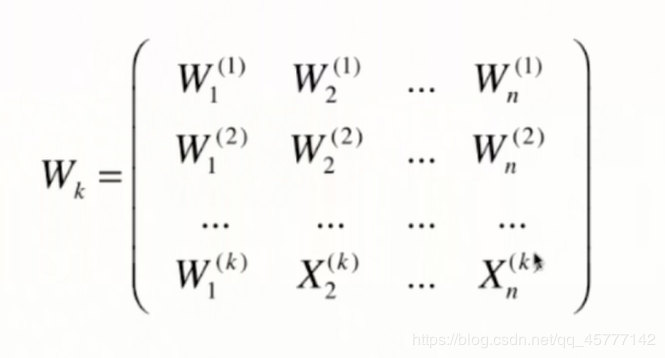假设 X 数据有m个样本，n个特征	此时 W 为针对 X 求出来的前K个主成分

如何将样本数据 X 从 n 维转换为 k 维？
想象一下，如果我们将 X 中的一个样本和 k个w 分别作点乘的话，那么我们的要的数据便是这个一个样本在k个方向上对应的每一个方向大小。正常情况下 k < n,说这样我们便完成了 n 维样本到 k 维的映射。矩阵相乘表示为：
X⋅WkT=XmX\cdot W^{T}_{k} = X_{m}X⋅WkT=Xm
下面我们实现PCA算法的源码：

import numpy as np
class PCA:
    def __init__(self, n_components):
        """初始化PCA"""
        assert n_components >= 1, "n_components must be valid"
        self.n_components = n_components
        self.components_ = None
    def fit(self, X, eta=0.01, n_iters=1e4):
        """获得数据集X的前n个主成分"""
        assert self.n_components <= X.shape[1], \
            "n_components must not be greater than the feature number of X"
        def demean(X):
            return X - np.mean(X, axis=0)
        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)
        def df(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)
        def direction(w):
            return w / np.linalg.norm(w)
        def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):
            w = direction(initial_w)
            cur_iter = 0
            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if (abs(f(w, X) - f(last_w, X)) < epsilon):
                    break
                cur_iter += 1
            return w
        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w
            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
        	return self
        def transform(self, X):
        """将给定的X，映射到各个主成分分量中"""
        assert X.shape[1] == self.components_.shape[1]
       		return X.dot(self.components_.T)
    	def inverse_transform(self, X):
        """将给定的X，反向映射回原来的特征空间"""
        assert X.shape[1] == self.components_.shape[0]
        	return X.dot(self.components_)
		def __repr__(self):
        	return "PCA(n_components=%d)" % self.n_components

紧接着我们自己通过测试来更感性的认识一下这个算法的强大：
小伙伴一定要记得把上述的Python代码（打包成PCA.py）和下面这个测试的放在一个目录下！！

import numpy as np 
import matplotlib.pyplot as plt            #导入我们所需要的包
X=np.empty((100,2))                        #随机创建一个我们需要的二维数组
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0.,10.,size=100)
from PCA import PCA
pca = PCA(n_components= 1)
pca.fit(X)
print(pca.components_)
'''此处得到的是我们所求的主成分的2个方向'''
X_reduction = pca.transform(X)
print(X_reduction.shape)
'''此时样本的2个特征已经降为一个特征,同样也可以将一维的恢复为原先的二维'''
X_restore = pca.inverse_transform(X_reduction)
print(X_restore.shape)
'''最后我们来可视化一下'''
plt.scatter(X[:,0],X[:,1],color = 'b',alpha = 0.5)
plt.scatter(X_restore[:,0],X_restore[:,1],color = 'r',alpha = 0.5)
plt.show()

可视化结果为：
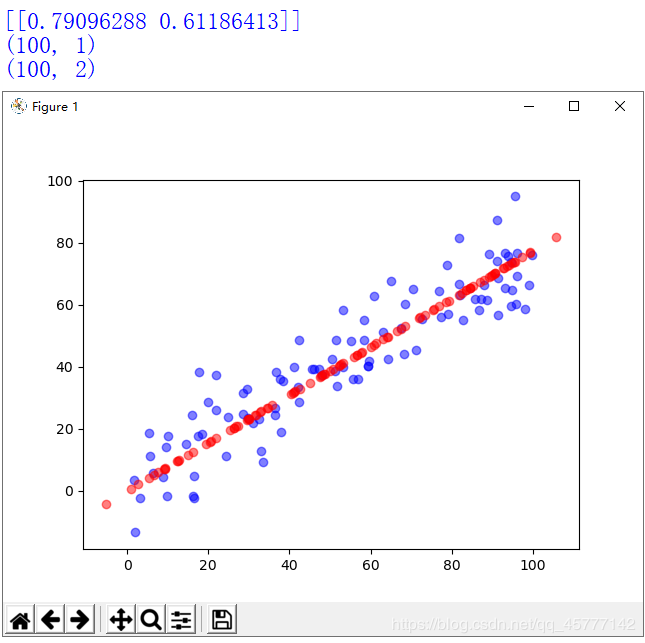
在这里插入图片描述
大家可以很清晰的看到紫色的离散点为原来二维数组中X的点，而红色的点映射成一条直线便是我们所求的降维后的主成分！！